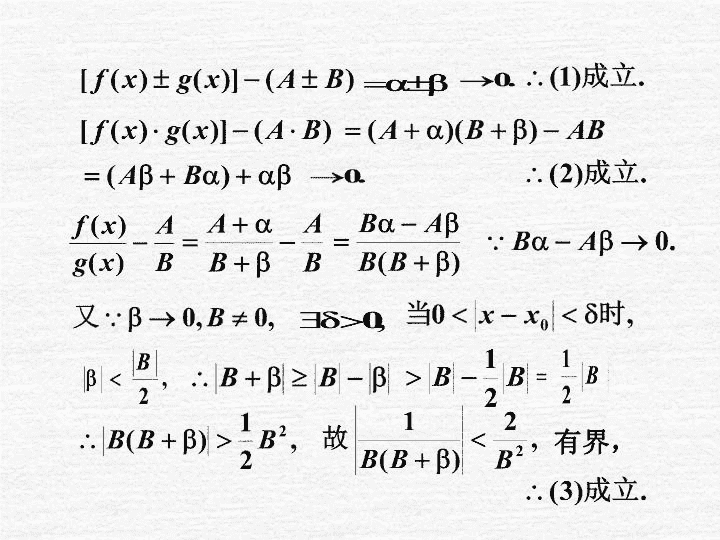最新微积分极限运算2ppt课件PPT课件 31页

'微积分极限运算2ppt课件 定理证由无穷小运算法则,得1.5极限的四则运算法则一、四则运算法则 解商的法则不能用由无穷小与无穷大的关系,得例2注：无穷大与非零有限数之积仍是无穷大；有限个无穷大之积仍是无穷大。 解例3(消去零因子法) 例4求极限解:（分子有理化）例5求极限解：原式（分子分母同时有理化）请思考解题方法. 有理分式函数求极限小结：（1）分母不等于零，直接用法则；（2）分母等于零，分子不等于零，无穷大（3）分母等于零，分子等于零，消去零因子，极限有可能存在无理分式函数求极限：一般先有理化,然后求极限. 例6求极限解通分注：无穷大之代数和是未定型。无穷大的商就是，也是未定型。 例7解(无穷小因子分出法) 有理分式的极限小结:2无穷小分出法:以分母中自变量的最高次幂除分子,分母,以分出无穷小,然后再求极限.1“抓大头”:分子分母中只考虑最高次幂项 练习： 例8求极限解有理化“抓大头” 解 例10解左右极限存在且相等, 小结1.极限的四则运算法则、复合函数极限及其推论;2.极限求法:(3)利用无穷小运算性质求极限(4)利用左右极限求分段函数极限.(1)分式函数极限求法时,用代入法(分母不为0)时,对型,约去公因子时,分子分母同除最高次幂“抓大头”(2)复合函数极限求法设中间变量 重点：运用极限的四则运算、复合函数的极限法则求极限难点：求极限的一些技巧，极限不存在时的一些运算 思考题1.在某个过程中，若有极限，无极限，那么是否有极限？是否有极限？为什么？3.试确定常数a使2.已知，则（）B必有C都不一定存在A必有D 4.已知在的一个邻域内有界，若，则必有（）ABC不能确定D极限不存在5.若与的极限均存在，则的极限如何？（）A必存在B必不存在C不一定存在D极限必为零 思考题解答假设有极限，由极限运算法则可知：必有极限，与已知矛盾，故假设错误．1.没有极限．有极限，不一定有极限．极限不存在．如 2.已知C都不一定存在正确选项为例如当时，极限均不存在。 3.解:令则故因此 4.已知在的一个邻域内有界，若，则必有（）C不能确定极限不存在正确选项为例如当时，当时， 5.若与的极限均存在，则的极限如何？（）A必存在B必不存在C不一定存在D极限必为零正确选项为C不一定存在例如极限不存在当时， 作业：P491（1、3、5、7、10、12、14）2（1、3），3，4,5 备用题设解:利用前一极限式可令再利用后一极限式,得可见是多项式,且求故 '