计量经济学课件PPT异方差.ppt 66页

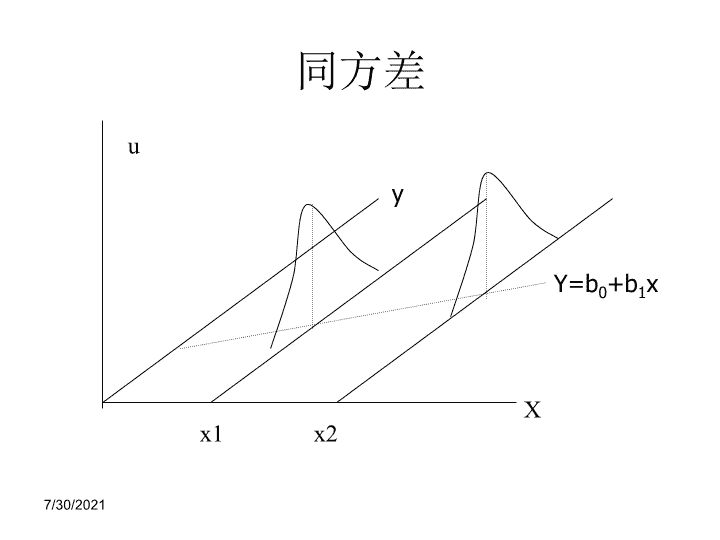
'异方差回顾线性回归模型假设假定1：在重复抽样中解释变量X是确定性变量——固定的（非随机，而且解释变量之间不相关）假定2：随机误差项具有0均值和同方差。即，E(ui|Xi)=0Var(ui|Xi)=2假定3：随机误差项在不同样本点之间是独立的。即，Cov(ui,uj)=0假定4：随机误差项与解释变量之间不相关。即，Cov(ui,Xi)=E(uiXi)=0假定5：随机误差项服从0均值、同方差的正态分布。即，ui~N(0,2)7/30/2021 第七章异方差模型违反5项基本假定之二——同方差，称为异方差。此时，LS估计量失去优良性。需要发展估计模型参数的补救方法。7/30/2021 x1x2Xu同方差yY=b0+b1x7/30/2021 异方差x1x2Xu随着x增加随机扰动项方差增大Y7/30/2021 主要内容一、异方差的定义二、产生异方差的背景三、异方差性的后果四、异方差性的检验五、异方差的处理（加权最小二乘法）（WLS）六、Eview处理异方差的步骤7/30/2021 一、异方差的定义异方差是相对于同方差而言的。异方差在横截面数据中比时间序列数据更为常见同方差：在经典线性回归模型的基本假定2中，随机扰动项ui的对每一个样本点的方差是一个等于2的常数，即：Var(ui)=2=常数i=1,2,…,n异方差：是指随机扰动项ui随着解释变量Xi的变化而变化，即：Var(ui)=2i=2f(Xi)i=1,2,…,n但ui仍然是一个服从正态分布的随机变量返回7/30/2021 二、产生异方差的背景一、按照边错边改学习模型（error-learningmodels），人们在学习的过程中，其行为误差随时间而减少。在这种情况下，预料的会减少。例如，随着打字练习小时数的增加，不仅平均打错个数而且打错个数的方差都有所下降。二、随着收入的增长，人们有更多的备用收入，从而如何支配他们的收入有更大的选择范围。因此，在做储蓄对收入的回归时，很可能发现，由于人们对其储蓄行为有更多的选择，与收入俱增。三、随着数据采集技术的改进，可能减少。四、异方差还会因为异常值的出现而产生。一个超越正常值范围的观测值或称异常值是指和其它观测值相比相差很多（非常小或非常大）的观测值。五、回归模型的设定不正确也会造成异方差。例如，在一个商品的需求函数中，若没有把有关的互补商品和替代商品的价格包括进来（忽略变量偏差），则回归残差就可能出现异方差。7/30/2021 产生异方差的三个实例1服装需求函数没有考虑气候因素，气候对q的影响包含在ui中高I拿出更多钱适应气候低I正是“可怜老汉衣正单心忧炭贱愿天寒”不同I对q的需求偏离程度不同，ui的方差随着收入增大而增大。2按收入分组数据的平均数建立的消费函数因为收入I服从正态分布截面数据中高、低收入组的家庭数少于中收入组，因观察个数不同造成各组平均数的方差呈现U型分布。（见下图）如果这种观测误差站随机误差项的主要部分，那么将随收入成规律变化。7/30/2021 siXi7/30/2021 3随机误差项方差与解释变量无关以某行业各个企业为样本建立生产函数解释变量中没有包括外部环境，那么各个企业外部环境对产出的影响，归入随机误差项。由于外部环境不同造成异方差，但这里的方差与解释变量无关，不呈现规律性。返回7/30/2021 三、异方差性的后果1、参数的OLS估计仍然是线性无偏的，但不是最小方差的估计量2、t检验失效3、降低预测精度由于异方差，会使得OLS估计的方差增大，从而造成预测误差变大，降低预测精度。7/30/2021 1、参数的OLS估计仍然是线性无偏的，但不是最小方差的估计量一元线性回归模型为例该形式具有最小方差该形式不具有最小方差7/30/2021 2、变量的显著性检验失效返回7/30/2021 四、异方差性的检验1、图解法2、集团法（双变量模型）3、帕克(Park)检验4、格莱泽(Glejser)检验5、White检验7/30/2021 1、图解法7/30/2021 如果对异方差的性质没有任何先验或经验信息,可先在无异方差的假定下做回归分析，然后对残差的平方2ˆiu做事后检查，看这些2ˆiu是否呈现系统性的样式。虽然2ˆiu不等于iuˆ，但可以作为替代变量，特别是样本含量足够大时。对2ˆiu的检查可能出现诸如上图所示的那样。在这些图中，2ˆiu是对应于iYˆ而描绘的，其目的是要找出Y的估计均值是否与平方残差有任何系统联系。图1未发现两个变量之间有任何系统性样式，表明数据中也许没有异方差。图2至5呈现一定的样式。例如，图3表示2ˆiu与iYˆ之间的一个线性关系，而图4和5则表示二次关系。7/30/2021 图示法及其类型异方差是指e的方差随着x的变化而变化。故可以根据x-y或残差x-e2的散点图，对异方差是否存在及其类型作出判断。异方差大致可分为三种：（1）递增异方差（2）递减异方差（3）复杂型异方差7/30/2021 7/30/2021 7/30/2021 7/30/2021 7/30/2021 怎样通过Eviews作x-y散点图Scatyx回车（作散点图的命令）其中y（第一位）是y轴，x（第二位）是x轴。并观察其是否成：（1）喇叭型或倒喇叭型（2）纺锤型或反纺锤型（3）以及其它有规则的图形（除线性条形）。以上三种均可能存在异方差。7/30/2021 怎样通过Eviews作x-e2散点图1、键入LSycx作回归2、键入GENRE1=resid调用残差3、键入GENRE2=E1^2生成残差平方4、键入SCATE2X或SCATE1X如果呈现出某种有规律的分布，说明残差中蕴涵作模型（1）未提取净的信息，或（2）可能存在异方差或自相关，或（3）设定有误。7/30/2021 1。纺锤型7/30/2021 2。反纺锤型7/30/2021 3。漏斗型7/30/2021 4。反漏斗型7/30/2021 5。其它有规律可寻的图形返回7/30/2021 2、集团法（Goldfeld-Quanttest）7/30/2021 3、帕克(Park)检验残差平方后取对数关于解释变量的对数值用LS进行模型估计，若解释变量系数显著，存在异方差7/30/2021 4、格莱泽(Glejser)检验格莱泽检验类似于帕克检验。格莱泽建议，在从OLS回归取得误差项后，使用ui的绝对值与被认为密切相关的解释变量再做LS估计，并使用如右的多种函数形式。若解释变量的系数显著，就认为存在异方差。7/30/2021 5、White检验的思路检验原模型是否存在异方差，先将估计原模型的残差平方，作为增强模型的被解释变量，原模型的所有右端变量的一次、二次和交叉乘积项作为被解释变量。并增强模型检验以下假设：H0：同方差、回归项相互独立和线性设定合理都成立HA：至少其中一个不满足因此，White检验是一种常规检验。只要有一项不成立，H0被拒绝，反之，若不拒绝，就本次而言，认为原模型还可以。7/30/2021 注释：还有其它一些检验方法，但总的来说还没有一个普遍适用的方法。返回7/30/2021 五、异方差的处理加权最小二乘法（WLS）思路根据误差最小建立起来的OLS法，同方差下，将各个样本点提供的残差一视同仁是符合情理的。各个ei提供信息的重要程度是一致的。但在异方差下，离散程度大的ei对应的回归直线的位置很不精确，拟合直线时理应不太重视它们提供的信息。即Xi对应的ei偏离大的所提供的信息贡献应打折扣，而偏离小的所提供的信息贡献则应于重视。因此采用权数对残差提供的信息的重要程度作一番校正，以提高估计精度。这就是WLS（加权最小二乘法）的思路。7/30/2021 加权最小二乘法的机理以递增型为例。设权术WI与异方差的变异趋势相反。Wi=1/2i。Wi使异方差经受了“压缩”和“扩张”变为同方差。7/30/2021 加权最小二乘法（WLS）异方差：是指随机扰动项ui随着解释变量Xi的变化而变化，即：Var(ui)=2i=2f(Xi)i=1,2,…,nWLS的思路是寻找“权数”，通过加权使原模型成为没有异方差的模型，再用OLS进行估计。7/30/2021 加权最小二乘法（WLS）的一般形式7/30/2021 加权矩阵W由何而来？采用OLS估计原模型：Y=XB+U得到残差，以各次观察残差的平方作为W权数矩阵主对角线上总体方差的近似值返回7/30/2021 异方差的处理正如已经看到的，异方差虽然不损坏LS估计量的无偏性和一致性，但却使它们不再是有效的。效率的缺乏使得通常的假设检验程序变得可疑，因此，补救措施显然是需要的。补救的方法可以分为两种：7/30/2021 1、加权最小二乘法WLS（WeightedLeastSquares）原理：通过对原模型加权，使之变成一个新的不存在异方差的模型，然后用OLS估计其参数。应用中直接采用加权最小二乘法WLS7/30/2021 2、1、采用OLS方法得到随机误差项的近似估计量来构成加权矩阵2、双变量模型中，2)(iiXXf=，或22)(iiXuVars=3、双对数模型将变量该用双对数形式可以减小异方差性。7/30/2021 （1）采用OLS方法得到随机误差项的近似估计量来构成加权矩阵实际操作中，首先对存在异方差的模型采用OLS方法得到随机误差项的近似估计量，以此构成加权矩阵的估计量，即，当我们应用计量经济学软件包时，只要选择加权最小二乘法，将上述矩阵输入，估计过程即告完成。这样，就引入了人们通常采用的经验方法，即并不对原模型进行异方差检验，而是直接选择加权最小二乘法，尤其是采用横截面数据作样本时。如果确实存在异方差性，则被有效地消除了；如果不存在异方差性，则加权最小二乘法等价于普通最小二乘法。7/30/2021 用P－1左乘左式，返回7/30/2021 六、EViews处理异方差的步骤1、用OLS估计模型，计算出残差RESID2、建立权数序列GENRW=1/ABS(RESID)大残差对应小权，小残差对应大权3、选择WLS方法（以W作权数修正模型）RESID*WRESID*（1/RESID）=1提供权数序列名w4、经验作法：对截面数据，直接采用WLS估计模型，存在异方差则消除异方差，否则WLS等价于OLS。7/30/2021 误差随E由大到小权数w由小到大大乘小，小乘大，加权为同方差加权最小二乘法的原理7/30/2021 加权最小二乘法的原理同方差7/30/2021 居民储蓄模型估计储蓄是居民的金融消费，也是满足相应收入水平的“基本生活”以后的扩展消费。从具体问题的经验分析，储蓄具有异方差特性。因此建立储蓄模型就不能使用最小二乘法。对于这类典型的异方差问题（提问：为什么是典型的？），我们应当怎样处理呢？7/30/2021 原始数据截面数据7/30/2021 储蓄Y与收入X的散点图7/30/2021 估计模型设定7/30/2021 估计结果7/30/2021 残差趋势图低、高收入组对应残差大7/30/2021 残差与收入的散点图（喇叭型）Genrer1=residscater1x7/30/2021 White检验线性关系成立并拒绝H0很可能是存在异方差7/30/2021 采用加权最小二乘法克服异方差GENRW=1/X生成权数序列w重新设定方程EQ1，单击OPTION选项按钮因为残差与收入的平方xi2项关系密切，所以采用平方项的开方的倒数1/x做权数。Var(ui)=2Xi2从中选择加权最小二乘法，指定权数序列名称w7/30/2021 估计选项7/30/2021 加权后拟合优度减少回归标准误也减少7/30/2021 克服异方差的另一办法—模型变换的过程与步骤GENRx1=1/xGenrxy=x/yLsxycx17/30/2021 模型变换法的估计结果回归标准误进一步降低7/30/2021 loadc:lx5yfch.wf1vector(10)m‘存放自由度、小样残差平方和、大样残差平方和、F检验值和F检验的概率值SORTX"按居民收入排序SMPL112"小数据样本m(1)=10equationsmleq.LSYCX"得ESS1m(2)=@ssrSMPL2031"大数据样本equationlrgeq.LSYCX"得ESS2m(3)=@ssrm(4)=m(3)/m(2)m(5)=@fdist(m(4),m(1),m(1))showm集团法（Goldfeld-Quanttest）的程序7/30/2021 7/30/2021 R110.00000R2162899.2R3769899.2R44.726231R50.010965R60.000000R70.000000R80.000000R90.000000R100.000000小概率程序运行结果H0:σ21=σ22HA:σ21≠σ22计算F统计量ESS1=162899.2ESS2=769899.2df=(31-7)/2-2=12-2=10F=(ESS2/df)/(ESS1/df)=4.726231F>Fo.o1(10,10)则随机扰动项存在异方差7/30/2021 人均消费函数处理某地年人均收入X和年人均消费Y的资料。要求：（1）用PARK检验是否存在异方差（2）用OLS估计消费函数（3）用WLS估计消费函数（4）比较两种方法得到的结果7/30/2021 残差呈纺锤型7/30/2021 分组资料7/30/2021 分组资料，且已知各组样本数分组资料且已知各组样本数N，一般用1/N做权数进行加权最小二乘法估计模型N每组户数，Y每组平均支出，X每组平均收入请用OLS和WLS拟合模型，并作对比。返回7/30/2021'