《全等三角形的判定课件PPT》ASA-AAS.ppt 30页

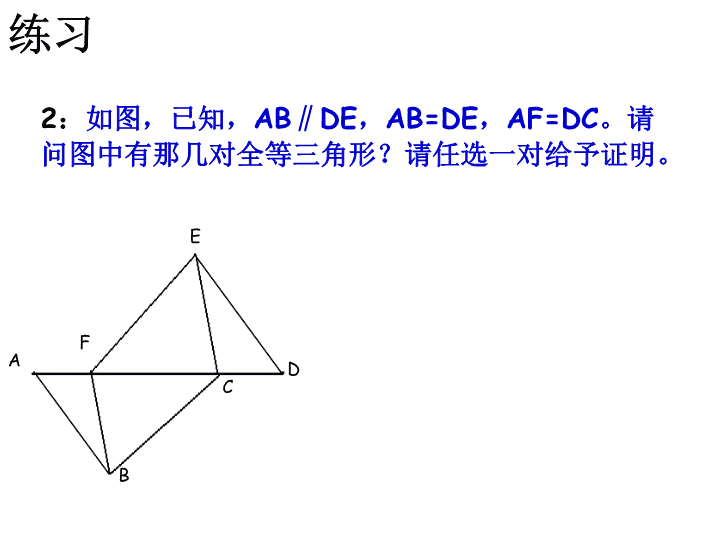
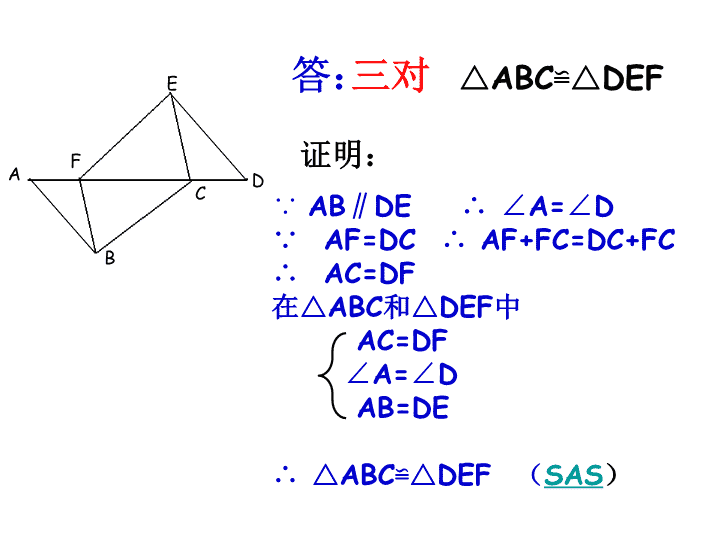
'1.我们已学了那些判定三角形全等的方法?复习边角边（SAS）：有两边和它们夹角对应相等的两个三角形全等。 练习2：如图，已知，AB∥DE，AB=DE，AF=DC。请问图中有那几对全等三角形？请任选一对给予证明。FEDCBA 练习FEDCBA答：证明：∵AB∥DE∴∠A=∠D∵AF=DC∴AF+FC=DC+FC∴AC=DF在△ABC和△DEF中AC=DF∠A=∠DAB=DE∴△ABC≌△DEF（SAS）△ABC≌△DEF三对 3、已知：如图11-全-1：一个三角形的两边分别是10和7，则第三边上的中线的取值范围是多少？ 一张教学用的三角形硬纸板不小心被撕坏了，如图，你能制作一张与原来同样大小的新教具吗？能恢复原来三角形的原貌吗？怎么办？可以帮帮我吗？创设情景,实例引入CBEAD 12.2全等三角形的条件（ASA）（AAS） 我们先来探究两角夹边对应相等时两个三角形是否全等先任意画一个△ABC，再画一个△DEF使得EF=BC，∠E=∠B，∠F=∠C；画法：1、画EF=BC2、画∠MEF=∠B;再画∠NFE=∠CEM、FN交于点D.DEFABCABCABCABCMN观察所得的两个三角形是否全等。 公理3（全等三角形判定2）有两个角和它们夹边对应相等的两个三角形全等用符号语言表达为：ABCDEF在△ABC与△DEF中∴△ABC≌△DEF（ASA）∠A=∠D∠B=∠EAB=DE(简写成“角边角”或“ASA”）。 如图：在△ABC和△DEF中，∠A=∠D，∠B=∠E，BC=EF，△ABC与△DEF全等吗？能利用角边角条件证明你的结论吗？探究2ABCDEF证明：∵∠A＋∠B＋∠C=180o∠D＋∠E＋∠F=180o∴∠C=∠F又∵∠A=∠D，∠B=∠E在△ABC和△DEF中∠B=∠E∠C=∠FBC=EF∴△ABC≌△DEF（ASA）有两个角和其中一个角的对边对应相等的两个三角形是否全等？ 有两个角和其中一个角的对边对应相等的两个三角形全等。公理2的推论ABCDEF用符号语言表达为：在△ABC和△DEF中∴△ABC≌△DEF（AAS）∠A=∠DBC=EF∠B=∠E(简写成“角角边”或“AAS”） 例题讲解：例1.已知：点D在AB上，点E在AC上，BE和CD相交于点O，AB=AC，∠B=∠C。求证：BD=CEAEDCBO如果把已知中的AB=AC改成AD=AE,那么BD和CE还相等么？为什么？思考 探究3有两个角对应相等，以及一个三角形中两个对应角的夹边与另一个三角形中一对应角的对边对应相等的两个三角形是否全等呢？ABCD观察如图：△ABC是直角三角形，∠ACB＝90o,CDAB,垂足为D。则在△ACD与△CBD中便有：∠A=∠1∠ADC=∠CDB=90oCD=CD试想△ACD与△CBD会全等吗？（1两个三角形并非有两角一边对应相等便能判别它们全等，只有满足（ASA）和（AAS）才行。 练习1．如图11-应12所示，已知E是AC的中点，CF∥AB．试说明：CF=AD．1234 例2.如图，∠1=∠2，∠3=∠4求证：AC=AD如果把已知中的∠3=∠4改成,∠D=∠C此题又如何?CAD1B23456 OACDBAO=BO1.如图，AB、CD相交于点O，已知∠A=∠B添加条件（填一个即可）就有△AOC≌△BOD还有吗？填一填1.如图，AB、CD相交于点O，已知∠A=∠B添加条件（填一个即可）就有△AOC≌△BOD1.如图，AB、CD相交于点O，已知∠A=∠B添加条件（填一个即可）就有△AOC≌△BODAC=BD?OC=OD?AC=OD?AC=OB?12√√×× 2．如图11-应-14所示，AB=CD，AD=BC，O为AC的中点，过O点的垂直线分别交AD、BC于M、N点．求证：(1)∠1=∠2．(2)AM=CN34 3：如图，已知E在AB上，∠1=∠2，∠3=∠4，那么AC等于AD吗？为什么？4321EDCBA 4321EDCBA解：AC=AD理由：在△EBC和△EBD中∠1=∠2∠3=∠4EB=EB∴△EBC≌△EBD(AAS)∴BC=BD在△ABC和△ABD中AB=AB∠1=∠2BC=BD∴△ABC≌△ABD(SAS)∴AC=AD 4.已知：如图，AB=CD，AD=BC，O是AC中点，OE⊥AB于E，OF⊥DC于F。求证：OE=OF。（9分） 5、如图，已知∠1=∠2，∠3=∠4，BD=CE求证：AB=AC4213ABCED6、如图，AB∥CD，AD∥BC，那么AB=CD吗？为什么？AD与BC呢？ABCD1234 7.如图，AB∥CD，AD∥BC，那么AB=CD吗？为什么？AD与BC呢？ABCD1234证明：∵AB∥CD，AD∥BC（已知）∴∠1＝∠2∠3＝∠4（两直线平行，内错角相等）∴在△ABC与△CDA中∠1＝∠2（已证）AC=AC（公共边）∠3＝∠4（已证）∴△ABC≌△CDA（ASA）∴AB=CDBC=AD（全等三角形对应边相等）五、思考题 8.已知:点E是正方形ABCD的边CD上一点，点F是CB的延长线上一点，且EA⊥AF，求证：DE=BFABCDEF 9.如图，要测量河两岸相对的两点A，B的距离，可以在AB的垂线BF上取两点C，D，使BC=CD，再定出BF的垂线DE，使A，C，E在一条直线上，这时测得DE的长就是AB的长。为什么？ABCDEF10、如图，已知∠1=∠2∠3=∠4求证：BD=CDABCDE1234 11．已知如图11-全-11所示，在△ABC中，AB=AC，∠BAC=90°，过A作直线ED，使ED⊥BE于E，CD⊥ED于D．求证：ED=BE+CD．（9分） 拓展题12.如图,已知AC∥BD，EA、EB分别平分∠CAB和∠DBA，CD过点E，则AB与AC+BD相等吗？请说明理由。ACEBD要证明两条线段的和与一条线段相等时常用的两种方法：1、可在长线段上截取与两条线段中一条相等的一段，然后证明剩余的线段与另一条线段相等。（割）2、把一个三角形移到另一位置，使两线段补成一条线段，再证明它与长线段相等。（补）F1234 13．如图11-全-2所示，点C是线段AB上任意点（C点与A、B点不重合），分别以AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE，AE与CD相交于点M，BD与CE相交于点N．求证：△ACE≌△DCB； 2714、已知：ΔABC和ΔBDE是等边三角形,点D在AE的延长线上。求证：BD+DC=ADABCDE分析：∵AD=AE+ED∴只需证：BD+DC=AE+ED∵BD=ED∴只需证DC=AE即可。12 15．如图11-全-7所示，已知AD是△ABC的中线，AE是△ABD的中线，AB=BD．求证：AC=2AE．F12345 15．如图11-全-7所示，已知AD是△ABC的中线，AE是△ABD的中线，AB=BD．求证：AC=2AE．证明：延长AE到F，使EF=AE，连接DF，在△AEB和△FED中，∴△AEB≌△FED，∴DF=AB，∠EDF=∠B．∵AD是△ABC的中线，AB=BD，∴CD=BD=AB=DF．又∵∠ADC=∠B+∠BAD，∠BAD=∠BDA，∠B=∠BDF，∴∠ADC=∠BDA+∠BDF=∠ADF．在△ACD和△AFD中，∴△ACD≌△AFD．∴AC=AF．又∵AF=2AE，∴AC=2AE． Goodbye!'