最新1.3-勾股定理的应用课件PPT.ppt 28页

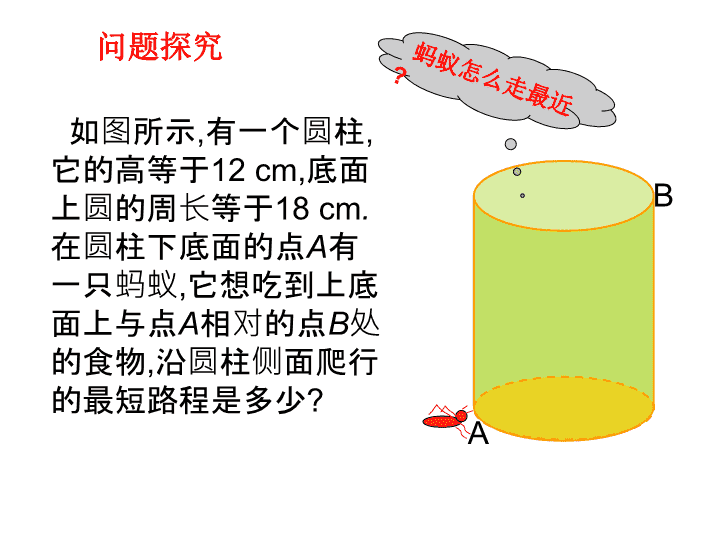
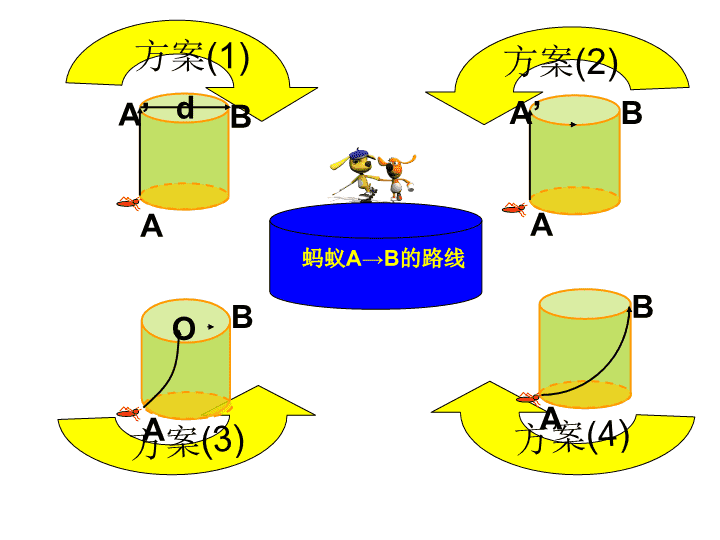
'1.3-勾股定理的应用 如图所示,有一个圆柱,它的高等于12cm,底面上圆的周长等于18cm.在圆柱下底面的点A有一只蚂蚁,它想吃到上底面上与点A相对的点B处的食物,沿圆柱侧面爬行的最短路程是多少?问题探究BA蚂蚁怎么走最近? 方案(1)方案(2)方案(3)方案(4)蚂蚁A→B的路线BAA’dABA’ABBAO 3、如图，是一个三级台阶，它的每一级的长、宽、高分别为2m、0.3m、0.2m，A和B是台阶上两个相对的顶点，A点有一只蚂蚁，想到B点去吃可口的食物，问蚂蚁沿着台阶爬行到B点的最短路程是多少？20.30.2ABABC2m(0.2×3＋0.3×3)m随堂练习 (2)小明随身只有一个长度为20cm的刻度尺,他能有办法检验边AD是否垂直于边AB吗?边BC与边AB呢?李叔叔想要检测雕塑(如图所示)底座正面的边AD和边BC是否分别垂直于底边AB,但他随身只带了卷尺.你能替他想办法完成任务吗?做一做(1)李叔叔量得边AD长是30cm,边AB长是40cm,点B,D之间的距离是50cm,边AD垂直于边AB吗? 例如图所示的是一个滑梯示意图,若将滑道AC水平放置,则刚好与AB一样长.已知滑梯的高度CE=3m,CD=1m,试求滑道AC的长.在Rt△ACE中,∠AEC=90°,由勾股定理得AE2+CE2=AC2,即(x-1)2+32=x2,解得x=5.故滑道AC的长度为5m.解:设滑道AC的长度为xm,则AB的长度为xm,AE的长度为(x-1)m. 本节课你学到了什么?感悟与反思 2.如图所示,将一根长24cm的筷子放入底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露在杯子外面的长度为hcm,则h的最小值是()A.12cmB.13cmC.11cmD.9cmC 拔尖自助餐在我国古代数学著作《九章算术》中记载了一道有趣的问题，这个问题的意思是：有一个水池，水面是一个边长为10尺的正方形，在水池的中央有一根新生的芦苇，它高出水面1尺，如果把这根芦苇垂直拉向岸边，它的顶端恰好到达岸边的水面，请问这个水池的深度和这根芦苇的长度各是多少？DABC 图（1）图（2）ABC下图是学校的旗杆,旗杆上的绳子垂到了地面,并多出了一段,现在老师想知道旗杆的高度,你能帮老师想个办法吗?请你与同伴交流设计方案?拔尖自助餐 解析:∵AB=6.5米,BC=2.5米,∠C=90°,∴AC2=AB2-BC2=62,∴AC=6米,∴地毯的长度为AC+BC=6+2.5=8.5(米),∴地毯的面积为8.5×6=51(平方米).故填51平方米.3.某楼梯的侧面视图如图所示,其中AB=6.5米,BC=2.5米,∠C=90°,楼梯的宽度为6米,因某种活动要求铺设红色地毯,则在AB段楼梯所铺地毯的面积应为.51平方米 2、一辆装满货物的卡车，其外形高2.5米，宽1.6米，要开进厂门形状如图的某工厂，问这辆卡车能否通过该工厂的厂门?说明理由。ABCD2米2.3米 ABMNOC┏D分析：H2米2.3米由于厂门宽度足够,所以卡车能否通过,只要看当卡车位于厂门正中间时其高度是否小于CH．如图所示,点D在离厂门中线0.8米处,且CD⊥AB,与地面交于H．随堂练习 4．如图1－2－11所示，已知四边形ABCD是正方形，四边形ACEF是矩形，M是线段EF的中点．求证：AM∥平面BDE. 【证明】设AC与BD的交点为O，连接OE.∵O，M分别是AC，EF的中点，四边形ACEF是矩形，∴四边形AOEM是平行四边形．∴AM∥OE.又∵OE⊂平面BDE，AM⊄平面BDE，∴AM∥平面BDE. 如图1－2－30，在正方体ABCD－A1B1C1D1中，E，F分别是棱AB，BC的中点，O是底面ABCD的中心，求证：EF⊥平面BB1O. 【证明】∵ABCD为正方形，∴AC⊥BO.又∵BB1⊥平面ABCD，AC⊂平面ABCD，∴AC⊥BB1，又∵BO∩BB1＝B，∴AC⊥平面BB1O，又EF是△ABC的中位线，∴EF∥AC，∴EF⊥平面BB1O. 如图1－2－41，AB是⊙O的直径，PA垂直于⊙O所在的平面，C是圆周上异于A、B的任意一点，求证：平面PAC⊥平面PBC. 【思路探究】由C是圆周上异于直径AB的点―→AC⊥BC―→由PA垂直于⊙O所在的平面―→PA⊥BC―→BC⊥平面PAC―→平面PAC⊥平面PBC. 【自主解答】连接AC，BC，则BC⊥AC，又PA⊥平面ABC，∴PA⊥BC，而PA∩AC＝A，∴BC⊥平面PAC，又BC⊂平面PBC，∴平面PAC⊥平面PBC. 面面垂直的判定定理是证明面面垂直的常用方法，即要证面面垂直，只需转证线面垂直，关键是在其中一个平面内寻找一直线与另一个平面垂直． 如图1－2－42，在四棱锥P－ABCD中，底面为正方形，侧棱PA＝PC.求证：平面PAC⊥平面PBD. 【证明】设AC∩BD＝O，连接PO，因为PA＝PC，所以PO⊥AC，又因为四边形ABCD为正方形，所以BD⊥AC，因为PO，BD⊂平面PBD，PO∩BD＝O，所以AC⊥平面PBD.因为AC⊂平面PAC，所以平面PAC⊥平面PBD. 4．如图1－2－47，四棱锥P－ABCD中，PA⊥平面ABCD，底面ABCD为直角梯形，AB⊥AD，CD⊥AD，求证：平面PDC⊥平面PAD. 【证明】∵PA⊥平面ABCD，∴PA⊥CD，又CD⊥AD，PA∩AD＝A，∴CD⊥平面PAD.又CD⊂平面PDC，∴平面PDC⊥平面PAD.'