最新18.1.1平行四边形的性质课件PPT.ppt 25页

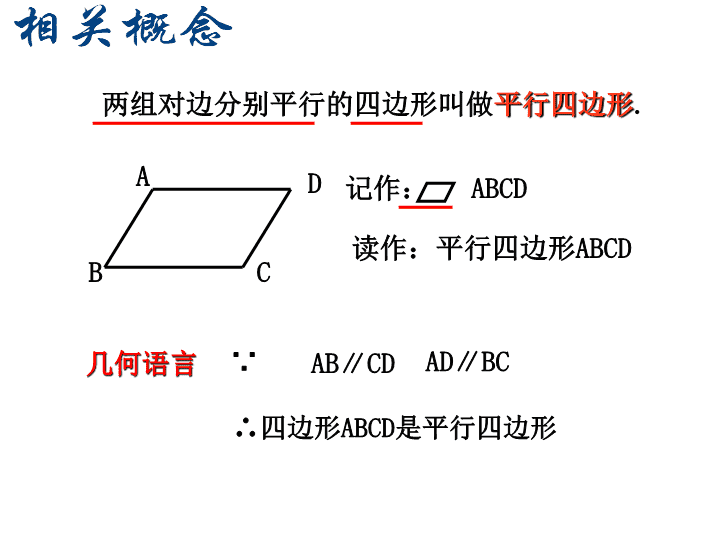
'18.1.1平行四边形的性质 下面的图片中，有你熟悉的哪些图形？ 两组对边分别平行的四边形叫做平行四边形.读作：平行四边形ABCDADBC记作：ABCDAB∥CDAD∥BC∵∴四边形ABCD是平行四边形几何语言 已知：ABCD求证：AB=CD，BC=DA；∠B=∠D，∠A=∠C.ABCD证一证1234即∠BAD＝∠DCB∵四边形ABCD是平行四边形∴AB∥CDAD∥BC，∴∠1＝∠2，∠3＝∠4∠1＝∠2AC＝CA∠3＝∠4∴△ABC≌△CDA（ASA）∴AB＝CD，BC＝DA，∠B＝∠D又∵∠1＝∠2，∠3＝∠4∴∠1＋∠4＝∠2＋∠3在△ABC和△CDA中证明：连接AC 平行四边形的性质平行四边形的对边相等；ABCD平行四边形的对角相等；∵四边形ABCD是平行四边形∵四边形ABCD是平行四边形平行四边形的对边平行；∵四边形ABCD是平行四边形AB∥CD，AD∥BC 典型例析（一）1、如图：ABCD中，EF∥AB，ABCDFE①则图中有＿＿个平行四边形；②若GH∥AD，EF与GH交于点O，则图中有＿＿个平行四边形。GHO39 典型例析（二）例：如图，在若∠A=130°，则∠B=______、∠C=______、∠D=______ABCD中，A:基础知识：B:变式训练：1、若∠A+∠C=200°，则∠A=______、∠B=______2、若∠A:∠B=5:4，则∠C=______、∠D=______CDAB50°130°50°100°80°100°80° C:拓展延伸：例：如图，在ABCD中，1、∠A:∠B:∠C:∠D的度数可能是()A、1:2:3:4B、3:2:3:2C、2:3:3:2D、2:2:3:3CDAB2、连接AC,若∠D=80°,∠DAC=40°则,∠B=___∠BAC=____,3、若AE、AF为高，且∠EAF=60°则∠C=——，∠B=——.CDABEFB80°60°120°60° 例：如图在ABCD中A基础知识：1、若AB=1㎝，BC=2㎝则ABCD的周长=______2、若AB=4㎝，BC=______ABCD的周长为18㎝，B变式训练：1、若AB：BC=3：4，周长为14㎝，则CD=——，DA=——2、若AB：BC=3：4，AB=6㎝，则BC=____，周长=_____C拓展延伸：若AB=x-4，BC=x+3，CD=6㎝，则AD=______CDAB6cm5cm3cm4cm8cm28cm13cm典型例析（三） AB=5，BC=9，BE平分∠ABC，4ABCD中，1、如图，则DE=_________ADCBE123典型例析（四） ABCD2、如图，ABCD中，BC=5，AC=4，∠BAC=90.则ABCD的面积为12543 作业设计（必做题）（1）ABCD中∠A：∠B=1：2则∠C=度，∠D=度（2）ABCD中，外角∠CBE=70°，则∠D=度CDEBA（3）ABCD中AB=a，BC=b，则ABCD周长为601201102(a+b) （1）如图ABCD中AB=5，BC=9，BE，CF分别平分∠ABC，∠BCD，则DE=_____，AF=_____，EF=_____作业设计（选做题）EFADCB（2）如图ABC，AB=AC=10，ADEF周长为_____BACDFE44120 (1)、如图课外思考ABCD中，ABE的面积S，ADE，BCE则S与S1+S2的大小关系是____面积分别是S1，S2，BEDCAS1SS2 PD∥AB，PE∥AC，PF∥BC，则(2)等边ABC的边长为10，P为ABC内一点，PD+PE+PF的值为______DFPCEBA E(3)、如图，∠ABC=3∠C，点F在CB延长线上，FE⊥CD，AD=CE=1，则BF=______ABCD中CBFDA 圆柱体容器理论最优设计省市：山东省济南市学校：历城二中班级：高二18班作者名称：张子厚指导教师姓名：刘元芬 摘要众所周知，中国是一个人口大国，人口总数居世界第一。中国也是一个资源贫乏的国家，人均资源很少。所以，我们节约资源。节约资源可以不浪费资源。我小组本次探究的是如何利用最少的材料制作最大的容器，（如水杯，垃圾桶等）这对节约资源有重大意义。注：因生活中许多容器都设计为圆柱体，故本次探究的容器也为圆柱体设计当所用材料一定时如何使容积最大。 正文1 正文2N=M/h+2M/r≥2√2M²/hr当M/h=2M/r时等号成立R=2hd=4h底面直径为高的四倍时使用材料最少。三．设容积为M，所用材料为NM=πr²hN=2πr²+2πrh①材料一定，容积最大M=πr²h①N=2πr²+2πrh②πr=N/(2r+2h)③③代入①M=Nrh/(2r+2h)=N/(2/h+2/r)≤N/2√(4/hr)当2/h=2/r等号成立h=r当底面直径为高的2倍时容积最大 正文3四．容积一定，材料最少N=2πr²+2πrh①M=πr²h②πr=M/rh③③代入①N=2M/h+2M/r≥2√(4M²/hr)当2/h=2/r时等号成立r=h底面直径为高的两倍时使用材料最少。 结论结论：当所用圆柱体容器无盖时，使容器底面直径为高的四倍最为经济。当所用圆柱体容器有盖时，使容器底面直径为高的两倍时最为经济应用无盖容器：可应用于家用水杯，碗，盆的制造。有盖容器：可应用于锅、垃圾桶，圆柱体包装的制造意义：应用这一理论能够最大限度地节约材料，降低了生产成本，对于节约资源有很大意义。参考文献：无'