最新《立体的截交线》PPT课件课件PPT.ppt 71页

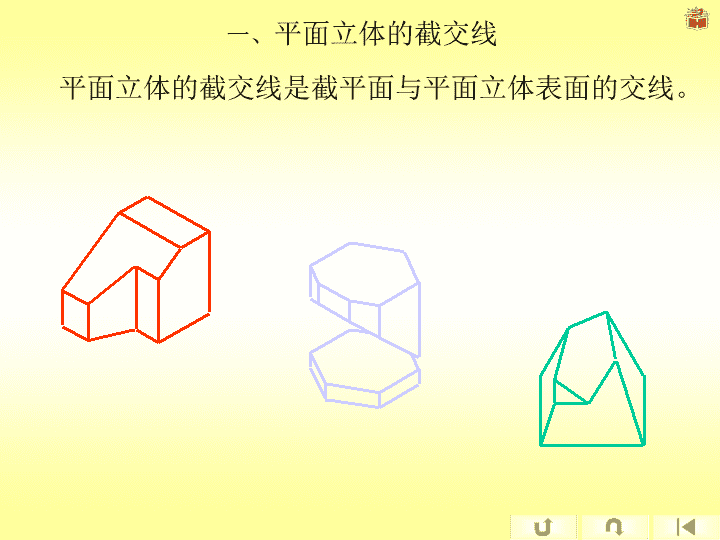
'《立体的截交线》PPT课件 4.7.1平面立体的切割一、平面立体的截交线二、平面立体截交线的性质三、平面立体截交线的求法1．棱柱上截交线的求法2．棱锥上截交线的求法平面立体的截交线是截平面与平面立体表面的交线。 一、平面立体的截交线平面立体的截交线是截平面与平面立体表面的交线。 [例题2]求立体切割后的投影431265ⅠⅥⅤⅣⅢⅡ114565234（6）（2）（3） [例题3]求立体截割后的投影7"11"8"87111"2"10"5"6"9"4"3"961（3）2（4）105ⅠⅪⅡⅨⅩⅣⅢ1"（2"）8"3"（4"）10"（5"）9"11"（6"）（7"） 2．棱锥上截交线的求法例题4例题5 [例题4]求立体切割后的投影23541116654326ⅠⅤⅣⅢⅡⅥ4（5）2（3） [例题5]求立体切割后的投影1（2）3412642156346（5）3（4）ⅢⅠⅥⅣⅡⅤ 回转体截交线一、截交线的性质二、截交线的类型及形状三、求作截交线的方法四、截交线上的特殊点五、作图步骤 一、曲面立体截交线的性质 二、截交线的类型及形状 三、求作截交线的方法 四、特殊点 五、作图步骤 4.7.2平面与圆柱相交一、平面与圆柱相交所得截交线形状二、求圆柱截交线上点的方法三、例题 一、平面与圆柱相交所得截交线形状矩形椭圆圆 二、求圆柱截交线上点的方法 三、例题 [例题1]求圆柱截交线11"1"5"4"8"8"83254ⅥⅦⅢⅡⅣⅤⅠⅧ4"5"2"3"2"3"解题步骤1．分析截平面为正垂面，截交线的侧面投影为圆，水平投影为椭圆；2．求出截交线上的特殊点Ⅰ、Ⅳ、Ⅴ、Ⅷ；3．求出若干个一般点Ⅱ、Ⅲ、Ⅵ、Ⅶ；4．光滑且顺次地连接各点，作出截交线，并且判别可见性；5．整理轮廓线。766"7"6"7" [例题2]求圆柱截交线解题步骤1．分析侧面投影为圆的一部分，截交线的水平投影为椭圆的一部分；2．求出截交线上的特殊点Ⅰ、Ⅱ、Ⅲ；3．求出若干个一般点Ⅳ、Ⅴ；4．光滑且顺次地连接各点，作出截交线，并且判别可见性；5整理轮廓线。3453"3"4"5"5"4"1"2"2"1"12 2"1"4"3"[例题3]求圆柱截交线解题步骤1．分析截交线的水平投影为直线和部分圆，侧面投影为矩形；2．求出截交线上的特殊点Ⅰ、Ⅱ、Ⅲ、Ⅳ；3．顺次地连接各点，作出截交线并判别可见性；4．整理轮廓线。1"2"133"4"24 1"2"3"4"[例题4]求圆柱截交线解题步骤1分析截交线的水平投影为直线和部分圆，侧面投影为矩形；2求出截交线上的特殊点Ⅰ、Ⅱ、Ⅲ、Ⅳ；3顺次地连接各点，作出截交线并判别可见性；4整理轮廓线。1"2"3"4"1324 [例题5]求圆柱截交线解题步骤1．分析截交线为矩形、椭圆及圆和直线的组合；截交线的水平投影为已知，侧面投影为矩形、椭圆和直线的组合；2．求出截交线上的特殊点Ⅰ、Ⅱ、Ⅲ、Ⅳ；3．求一般点Ⅴ；4．顺次地连接各点，作出截交线，并且判别可见性；5．整理轮廓线。3"31"122"4"455"3"2"5"1"4" [例题6]想象出物体及其侧面投影的形状 4.7.3平面与圆锥相交一、平面与圆锥相交所得截交线形状二、圆锥截交线的求法三、例题 一、平面与圆锥相交所得截交线形状圆椭圆三角形双曲线加直线段抛物线加直线段 二、求圆锥截交线上点的方法 三、例题 [例题1]求圆锥截交线解题步骤1．分析截平面为正垂面，截交线为椭圆；截交线的水平投影和侧面投影均为椭圆；2．求出截交线上的特殊点Ⅰ、Ⅱ、Ⅲ、Ⅳ；3．求出一般点Ⅴ；4．光滑且顺次地连接各点，作出截交线，并且判别可见性；5．整理轮廓线。3"33 [例题2]求圆锥截交线解题步骤1．分析截平面为正平面，截交线为双曲线；截交线的水平投影和侧面投影已知，正面投影为双曲线并反映实形；2．求出截交线上的特殊点A、C；3．求出一般点B；4．光滑且顺次地连接各点，作出截交线，并且判别可见性；5．整理轮廓线。a"a"acbb"b"c"c" [例题3]求圆锥截交线解题步骤1．分析截平面为正垂面侧平面，截交线为部分椭圆和梯形的组合；其水平投影为部分椭圆和直线的组合，侧面投影为部分椭圆和梯形的组合；2．求出截交线上的特殊点Ⅰ、Ⅱ、Ⅲ；3．出一般点Ⅳ、Ⅴ；4．光滑且顺次地连接各点，作出截交线，并且判别可见性；5．整理轮廓线。a2314"5"1"1"a"2"3"2"3"544"5" [例题4]分析圆锥切割后截交线投影的形式 [例题5]分析并想象出圆锥穿孔后的投影 4.7.4平面与圆球相交一、平面与圆球相交所得截交线形状二、求圆球截交线点的方法三、例题 一、平面与圆球相交所得截交线形状圆 二、求圆球截交线上点的方法 三、圆球截交线例题 [例题1]求圆球截交线解题步骤1．分析截平面为正垂面，截交线为圆；截交线的水平投影和侧面投影均为椭圆；2．求出截交线上的特殊点Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ、Ⅶ、Ⅷ；3．求出若干个一般点A、B、C、D；4．光滑且顺次地连接各点，作出截交线，并且判别可见性；5．整理轮廓线。1"2"123"4"34565"6"787"8"a"b"c"d"bacd2"1"3"4"5"6"7"8"a"bc"d" 22"1[例题2]求圆球截交线解题步骤1．分析截平面为两个侧平面和一个水平面，截交线为圆弧和直线的组合；截交线的水平投影和侧面投影均为圆弧和直线的组合；2．求出截交线上的特殊点Ⅰ、Ⅱ；3．求出各段圆弧；4．判别可见性，整理轮廓线。33"3"1"2" [例题3]求圆球截交线 [例题4]分析并想象出圆球穿孔后的投影 §10-5综合题 [例题1]分析并想象出物体的投影 [例题2]求出物体切割后的投影3"333" [例题3]分析并想象出物体切割后的投影 本章结束 14.1.4整式的乘法第4课时整式的除法 创设情境问题：木星的质量约是1.90×1024吨，地球的质量约是5.97×1021吨.你知道木星的质量约为地球质量的多少倍吗？(1.90×1024)÷(5.97×1021) 说说你计算的根据是什么？讨论：(1)计算(1.90×1024)÷(5.97×1021)创设情境解：原式=(1.90÷5.97)×(1024÷1021)≈0.318×103≈3.18×102 （2）你能利用（1）中的方法计算下列各式吗？8a3÷2a；6x3y÷3xy；12a3b2x3÷3ab2（3）你能根据（2）说说单项式除以单项式的运算法则吗？创设情境 探究新知1.观察讨论：(2)中的三个式子是什么样的运算？都是单项式除以单项式的运算.2.思考一下可不可以用自己现有的知识和数学方法解决“讨论”中的问题呢？可以从两方面考虑 1.从乘法与除法互为逆运算的角度去考虑.(1)可以想象5.97×1021×()=1.90×1024.根据单项式与单项式相乘的运算法则联想：所求单项式的系数乘5.97等于1.90，所以所求单项式的系数为1.90÷5.7≈0.318，所求单项式的幂值部分应包含1024÷1021即103.探究新知 由此可知5.97×1021×(0.318×103)≈1.90×1024所以(1.90×1024)÷(5.97×1021)≈0.318×103探究新知 (2)可以想象2a·()=8a3,根据单项式与单项式相乘的法则，可以考虑：8÷2=()；a3÷a=()即2a·()=8a3所以8a3÷2a=()探究新知4a24a24a2 同样的道理：3xy·()=6x3y;3ab2·()=12a3b2x3所以：6x3y÷3xy=2x2;12a3b2x3÷3ab2=4a2x3探究新知2x24a2x3 2.还可以从除法的意义去考虑.探究新知 (2)8a3÷2a==4a2探究新知6x3y÷3xy==2x212a3b2x3÷3ab2==4a2x3 观察上述几个式子的运算，你发现它们有什么共同特征？（2）运算结果都是把系数、同底数幂分别相除后作为商的因式；对于只在被除式里含有的字母，则连同它的指数一起作为商的一个因式.探究新知（3）单项式相除是在同底数幂除法的基础上完成的.（1）都是单项式除以单项式 例1计算(1)28x4y2÷7x3y；(2)-5a5b3c÷15a4b；(3)（2x2y）3·（-7xy2)÷14x4y3；(4)5(2a+b)4÷(2a+b)2.探究新知 解：(1)28x4y2÷7x3y=(28÷7)x4-3y2-1=4xy(2)-5a5b3c÷15a4b=(-5÷15)a5-4b3-1c=ab2c(3)（2x2y）3·（-7xy2)÷14x4y3(4)5(2a+b)4÷(2a+b)2=5(2a+b)2=8x6y3·（-7xy2)÷14x4y3=-56x7y5÷14x4y3=-4x3y2探究新知-13 再探新知(1)(am+bm)÷m；(2)(a2+ab)÷a；(3)(4x2y+2xy2)÷2xy.1.计算下列各式： 你是怎样计算的？还有什么发现吗？解：(1)(am+bm)÷m=a+b(2)(a2+ab)÷a=a+b(3)(4x2y+2xy2)÷2xy=2x+y再探新知 归纳法则：多项式除以单项式，先把这个多项式的每一项除以这个单项式，再把所得的商相加.你能把这句话写成公式的形式吗？(am+bm)÷m=am÷m+bm÷m=a+b 计算：(1)(12a3-6a2+3a)÷3a=12a3÷3a-6a2÷3a+3a÷3a=4a2-2a+1巩固练习 (2)(21x4y3-35x3y2+7x2y2)÷(-7x2y)=21x4y3÷(-7x2y)-35x3y2÷(-7x2y)+7x2y2÷(-7x2y)=-3x2y2+5xy-y巩固练习 （3）[(x+y)2-y(2x+y)-8x]÷2x=(x2+2xy+y2-2xy-y2-8x)÷2x=(x2-8x)÷2x巩固练习 课堂小结单项式除以单项式、多项式除以单项式的计算过程中应注意的事项有哪些？1.单项式除以单项式2.多项式除以单项式 作业教材第104页练习第2，3题习题14.1第6题'