金属及各类晶体配位数计算图总结课件PPT.ppt 191页

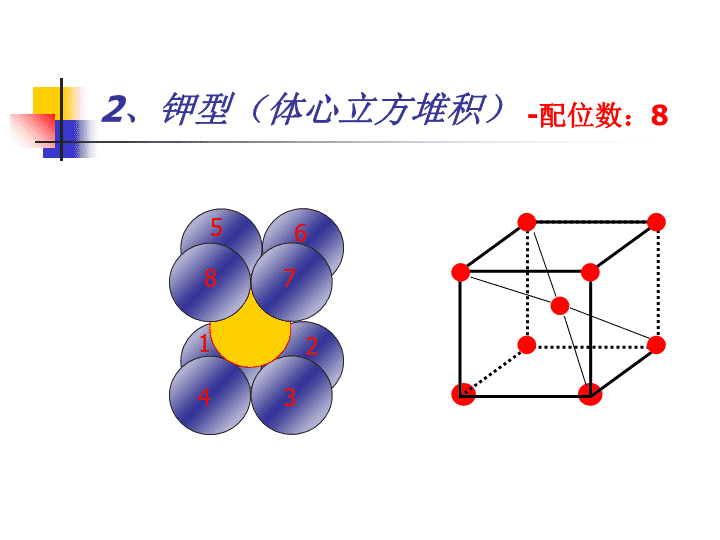
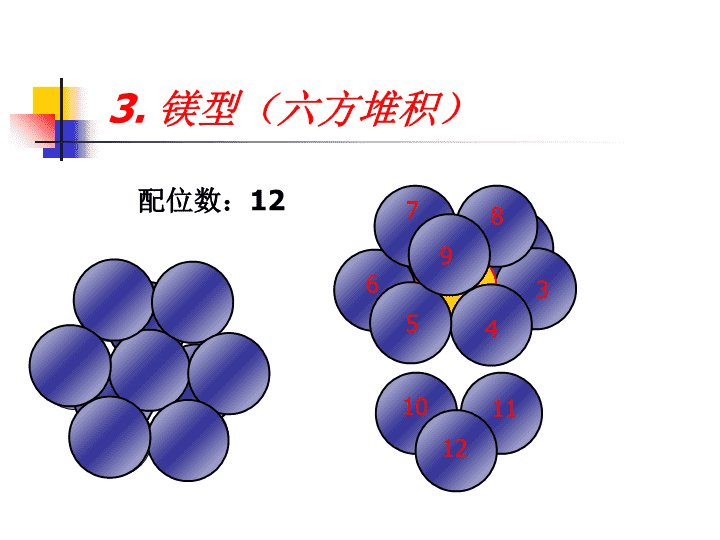
'金属及各类晶体配位数计算图总结 2、钾型（体心立方堆积）12345678-配位数：8 3.镁型（六方堆积）123456789101112配位数：12 2.立方密堆积(立方密积)(1)堆积形式如图所示：ABCABC…组合(2)堆积特点层的垂直方向为三次象转轴。既是立方体的空间对角线。原胞当中包含一个粒子，是布拉菲格子。 3.典型结构的配位数(1)六角密积和立方密积的配位数都是十二。即晶体中最大配位数为十二。(2)当晶体不是由全同的粒子组成时，相应的配位数要发生变化—减小。由于晶体的对称性和周期性的特点，以及粒子在结合成晶体时，是朝着结合能最小、最稳固的方向发展。因此，相应的配位数只能取:8(CsCl型结构)、6(NaCl型结构)、4(金刚石型结构)、3(层状结构)、2(链状结构)。 4.氯化铯型结构的配位数如图所示，大球(半径为R)中心为立方体顶角，小球(半径为r)位于立方体的中心。如果大球相切，则立方体的边长为：空间对角线的长度为： (1)如果小球恰好与大球相切，则小球的直径为：排列最紧密，结构最稳定。(2)如果小球直径大于0.73R,则小球可以与大球相切,而大球则不再相切。 (3)如果小球直径小于0.73R,则小球不能与大球相切,小球在中心可以摇动，结构不稳定，以致不能存在，于是结构将取配位数较低的排列(配位数为6的排列)。5.氯化钠型结构的配位数(1)如图所示，大球(半径为R)相切，小球(半径为r)也与大球相切。排列最紧密，结构最稳定。 (2)如果小球直径大于0.41R,则小球可以与大球相切,而大球则不再相切。(3)如果小球直径大于0.73R,则变成氯化铯结构。(4)如果小球直径小于0.41R,则小球不能与大球相切,小球在中心可以摇动，结构不稳定，以致不能存在，于是结构将取配位数较低的排列(配位数为4的排列)。 配位数r/R12181～0.7360.73～0.4140.41～0.2330.23～0.16配位数和半径之比的关系 配位数的确定高考备考 NaCl晶体中阴离子的配位数为6，而Cl-按面心立方堆积的配位数是12。怎么都是配位数一会儿是6，一会儿又是12，这怎么理解？氯离子按面心立方堆积是没错，但那不是真正的配位数，因为氯离子是同号离子，是相互斥的；同理，钠离子也是按面心立方堆积的，这两种离子形成的面心立方堆积都产生八面体空穴，彼此进入对方八面体空穴中就对了，此时异号离子之间的接触才算配位数，这样配位数就是真正的配位数，即6。面心立方堆积如果是金属原子，则其配位数是12，因为周围的原子都与该原子形成金属键的，这时也是真正的配位数。 我们在提到配位数时应当分析其所处环境。1、在晶体学中配位数与晶胞类型有关；2、离子晶体中指一个离子周围最近的异电性离子的数目；3、配位化学中，化合物中性原子周围的配位原子的数目。 一、晶胞密堆积、配位数1.配位数一个粒子周围最近邻的粒子数称为配位数。它可以描述晶体中粒子排列的紧密程度，粒子排列越紧密，配位数越大，结合能越低，晶体结构越稳定。2.密堆积如果晶体由完全相同的一种粒子组成，而粒子被看作小圆球，则这些全同的小圆球最紧密的堆积称为密堆积。密堆积特点：结合能低，晶体结构稳定；配位数最大为12。 第一层：每个球与6个球相切，有6个空隙，如编号1,2,3,4,5,6。第二层：占据1,3,5空位中心。第三层：在第一层球的正上方形成ABABAB······排列方式。(1)六角密积（Be,Mg,Cd,Zn）AB 基元由两个原子组成，一个位于(000)，另一个原子位于，六角密积是复式晶格，其布拉维晶格是简单六角晶格。 (2)立方密积（Au，Ag，Cu，Al，Ni）第一层：每个球与6个球相切，有6个空隙，如编号为1,2,3,4,5,6。第二层：占据1，3，5空位中心。第三层：占据2，4，6空位中心，按ABCABCABC······方式排列，形成面心立方结构，称为立方密积。BAC层的垂直方向：立方体的对角线。 3.配位数的可能值配位数的可能值为：12(密堆积：fcc,hcp)，8(bcc,氯化铯型结构)，6(sc,氯化钠型结构)，4(ZnS,金刚石型结构)，3(石墨层状结构)，2(链状结构)。 4.致密度如果把等体积的硬球放置在晶体结构中原子所在的位置上，球的体积取得尽可能大，以使最近邻的球相切，我们把一个晶胞中被硬球占据的体积与晶胞体积之比称为致密度(堆积比率，堆积因子，最大空间利用率)。 晶胞体积晶胞中原子所占体积设晶格常量为a，原子半径为R，则例1：求面心立方的致密度。N是晶胞中原子个数4 典型的晶体结构42CsClCs+1Cl-11288结构晶胞中的原子个数最近邻距离配位数 典型的晶体结构结构晶胞中的原子个数最近邻距离配位数84金刚石ZnSNaClNa+4Cl-46 二、离子晶体一般离子晶体配位数由阴阳离子半径决定：一般来说半径比（rˉ/r+)在0.2~0.4之间的，配位数为4；0.4~0.7之间，配位数为6；0.7~1.0之间的，配位数为8。配位数与r+/r-之比的关系:0.225----0.4144配位ZnS式晶体结构0.414----0.7326配位NaCl式晶体结构0.732----1.0008配位CsCl式晶体结构 CsCl型离子晶体:所属晶系:立方;点阵:立方P;结构基元及每个晶胞中结构基元的数目:CsCl,1个;Cs离子的配位数是8，Cl离子的配位数也是8。 NaCl型离子晶体:所属晶系:立方;点阵:立方F;结构基元及每个晶胞中结构基元的数目:NaCl,4个;Na和Cl离子的配位数都是6； 立方ZnS型离子晶体:所属晶系:立方;点阵:立方F;结构基元及每个晶胞中结构基元的数目:ZnS,4个;Zn和S离子的配位数都是4； CaF2型离子晶体:所属晶系:立方;点阵:立方F;结构基元及每个晶胞中结构基元的数目:CaF2,4个;Ca和F离子的配位数分别是8和4； 三、在配位化合物(简称配合物)中影响配位数的因素如下：1、中心原子的大小2、中心原子的电荷3、配体的性质 中心原子的大小中心原子的最高配位数决定于它在周期表中的周次。在周期表内,第1周期元素的最高配位数为2；第2周期元素的最高配位数为4；第3周期为6,以下为8、10。最高配位数是指在配合物中,中心原子周围的最高配位原子数,实际上一般可低于最高数。在实际中第1周期元素原子的配位数为2，第2周期不超过4。除个别例外，第3、4周期不超过6，第5、6周期为8。最常见的配位数为4和6,其次为2、5、8。配位数为奇数的通常不如偶数的普遍。 中心原子的电荷中心原子的电荷高，配位数就大。例如,等电子系列的中心原子Ag+、Cd2+和In3+与Cl-分别生成配位数为2、4和6的【AgCl2】-、【CdCl4】2-和【InCl6】3-配离子。同一元素不同氧化态的离子常具有不同的配位数,例如,二价铂离子Pt2+的配位数为4,而4价铂离子配位数Pt4+为6。 这是因为中心离子的电荷愈高,就需要愈多的配体负电荷来中和。中心原子的成键轨道性质和电子构型从价键理论的观点来说，中心原子成键轨道的性质决定配位数，而中心原子的电子构型对参与成键的杂化轨道的形成很重要,例如，Zn2+和Cu+离子的5个3d轨道是全满的,适合成键的是一个4s和3个4p轨道,经sp3杂化形成4个成键轨道，指向正四面体的四个角。因此，Zn2+和Cu+与CN-生成配位数为4的配离子【Zn(CN)4】2-和【Cu(CN)4】3-，并且是正四面体构型。 配体的性质同一氧化态的金属离子的配位数不是固定不变的,还取决于配体的性质。例如，Fe3+与Cl-生成配位数为4的【FeCl4】-，而与F-则生成配位数为6的【FeF6】3-。这是因为Fe3+从每个体积较大而较易极化的Cl-接受的电荷要大于体积较小而较难极化的F-。配合物的中心原子与配体间键合的性质，对决定配位数也很重要。在含F-的配合物中，中心原子与电负性很高的F-间的键合主要是离子键。如在B3+、Fe3+和Zr4+与F-的配合物中,随着中心原子半径的增加,配位数分别为4、6和7,主要受中心原子与配体的半径比的限制。很多配合物的中心原子与配体(例如CN-、SCN-、Br-、I-、NH3和CO等)间主要形成共价键，它们的配位数决定于中心原子成键轨道的性质。 配位场理论认为中心原子的内层轨道受周围配体的影响，也即关系到配位数。例如，Ni2+离子与H2O和NH3等具有小的相互排斥力的弱场配体，生成配位数为6的【Ni(H2O)6】2+和【Ni(NH3)6】2+等八面体配离子;与Br-和I-等具有大的相互排斥力的弱场配体则趋向于生成配位数为4的【NiBr4】2-和【NiI4】2-等正四面体配离子；与CN-等强场配体则生成配位数为4的【Ni(CN)4】2-平面正方形配离子。 中心离子（或原子）同单基配体结合的数目就是该中心离子（或原子）的配位数。例如[Cu(NH3)4]SO4中Cu离子的配位数为4，[Co(NH3)2（HO)4]Cl中Co离子的配位数为6。中心离子（或原子）同多基配体配合时，配位数等同于配位原子数目，例如[Cu(en)]中的乙二胺（en）是双基配体，因此Cu离子的配位数为4。 中心离子的配位数一般是2、4、6，最常见的是4和6，配位数的多少取决于中心离子和配体的性质──电荷、体积、电子层结构以及配合物形成时的条件，特别是浓度和温度。 一般来讲，中心离子的电荷越高越有利于形成配位数较高的配合物如Ag，其特征配位数为2，如[Ag(NH3)2]；Cu，其特征配位数为4，例[Cu(NH3)4]；Co，其特征配位数为6，例[Co(NH3)2（HO)4]。但配体电荷的增加对形成高配位数是不利的，因为它增加了配体之间的斥力，使配位数减少。如[Co(HO)6]同[CoCl4]相比，前者的配体是中性分子，后者是带负电荷的Cl离子，使Co的配位数由6降为4。因此，从电荷这一因素考虑，中心离子电荷的增高以及配位体电荷的减少有利于配位数的增加。 中心离子的半径越大，在引力允许的条件下，其周围可容纳的配体越多，配位数也就越大。例如Al与F可形成[AlF]配离子，体积较小的B(Ⅲ)原子就只能生成[BF]配离子。但应指出中心离子半径的增大固然有利于形成高配位数的配合物，但若过大又会减弱它同配体的结合，有时反而降低了配位数。如Cd可形成[CdCl]配离子，比Cd大的Hg，却只能形成[HgCl]配离子。显然配位体的半径较大，在中心离子周围容纳不下过多的配体，配位数就减少。如F可与Al形成[AlF]配离子，但半径比F大的Cl、Br、I与Al只能形成[AlX]配离子（X代表Cl、Br、I离子） 温度升高，常使配位数减小。这是因为热振动加剧时，中心离子与配体间的配位键减弱的缘故。而配位体浓度增大有利于形成高配位数的配合物。综上所述，影响配位数的因素是复杂的，是由多方面因素决定的，但对于某一中心离子在与不同的配体结合时，常具有一定的特征配位数。 二、金属晶体的原子堆积模型 金属晶体原子平面排列方式有几种？非密置层探究A143213642A5密置层配位数为4配位数为6 金属晶体的堆积方式──简单立方堆积非密置层层层堆积情况1：相邻层原子在同一直线上的堆积 简单立方堆积配位数：晶胞含金属原子数16例：（Po） 体心立方堆积非密置层层层堆积情况2：相邻原子层上层原子填入下层原子的凹穴中 体心立方堆积配位数：28晶胞含金属原子数:金属晶体的堆积方式──钾型 123456思考：第二层对第一层来讲最紧密的堆积方式有几种？123456AB，思考：对第一、二层来说，第三层可以最紧密的堆积方式有几种？密置层堆积方式不存在两层原子在同一直线的情况，只有相邻层紧密堆积方式，类似于钾型。123456 一种是将球对准第一层的球。123456123456另一种排列方式，是将球对准第一层的2，4，6位 下图是此种六方紧密堆积的前视图ABABA一种是将球对准第一层的球。123456于是每两层形成一个周期，即ABAB堆积方式，形成六方紧密堆积。 六方密堆积配位数：12。(同层6，上下层各3)晶胞含金属原子数:6金属晶体的堆积方式──镁型 第三层的另一种排列方式，是将球对准第一层的2，4，6位，不同于AB两层的位置，这是C层。123456123456123456 123456此种立方紧密堆积的前视图ABCAABC第四层再排A，于是形成ABCABC三层一个周期。配位数：12(同层6，上下层各3) 面心立方BCA晶胞含金属原子数:4金属晶体的堆积方式──铜型 堆积模型采纳这种堆积的典型代表配位数晶胞镁型MgZnTi12简单立方Po6钾型NaKFe8铜型CuAgAu12总结思考：4中模型单位体积容纳原子数大小关系？52%68%74%74%空间利用率 1.空间占有率等径球两种最密堆积具有相同的堆积密度，晶胞中圆球体积与晶胞体积之比称空间占有率，六方最密堆积（hcp）与立方最密堆积（ccp）空间占有率均为74.05％。 设圆半径为R，晶胞棱长为a，晶胞面对角线长                 则                 晶胞体积立方面心晶胞中含4个圆球，每个球体积为:立方最密堆积虽晶胞大小不同，每个晶胞中含球数不同。但计算得到空间占有率相同。 而体心立方堆积（bcp）则空间占有率低一些。体对角线长为晶胞体积体心立方晶胞含2个球 2、某些金属晶体(Cu、Ag、Au)的原子按面心立方的形式紧密堆积，即在晶体结构中可以划出一块正立方体的结构单元，金属原子处于正立方体的八个顶点和六个侧面上，试计算这类金属晶体中原子的空间利用率。 2）.立方面心结构立方面心结构的配位数＝12（即每个圆球有12个最近的邻居，同一层有六个，上一层三个，下一层三个）。立方密堆积中可以取出一个立方面心的单位来，每个单位中有四个圆球，球心的位置是000；01/21/2；1/201/2；1/21/20。等径圆球的最紧密堆积方式，在维持每个球的周围的情况等同的条件下，就只有上述两种，它们的空间利用率最高（74．05％）。 立方体边长=a"；立方体对角线＝        a"；四面体边长=        a"； 二、金属晶体的原子堆积模型 金属晶体原子平面排列方式有几种？非密置层探究A143213642A5密置层配位数为4配位数为6 金属晶体的堆积方式──简单立方堆积非密置层层层堆积情况1：相邻层原子在同一直线上的堆积 简单立方堆积配位数：晶胞含金属原子数16例：（Po） 体心立方堆积非密置层层层堆积情况2：相邻原子层上层原子填入下层原子的凹穴中 体心立方堆积配位数：28晶胞含金属原子数:金属晶体的堆积方式──钾型 123456思考：第二层对第一层来讲最紧密的堆积方式有几种？123456AB，思考：对第一、二层来说，第三层可以最紧密的堆积方式有几种？密置层堆积方式不存在两层原子在同一直线的情况，只有相邻层紧密堆积方式，类似于钾型。123456 一种是将球对准第一层的球。123456123456另一种排列方式，是将球对准第一层的2，4，6位 下图是此种六方紧密堆积的前视图ABABA一种是将球对准第一层的球。123456于是每两层形成一个周期，即ABAB堆积方式，形成六方紧密堆积。 六方密堆积配位数：12。(同层6，上下层各3)晶胞含金属原子数:6金属晶体的堆积方式──镁型 第三层的另一种排列方式，是将球对准第一层的2，4，6位，不同于AB两层的位置，这是C层。123456123456123456 123456此种立方紧密堆积的前视图ABCAABC第四层再排A，于是形成ABCABC三层一个周期。配位数：12(同层6，上下层各3) 面心立方BCA晶胞含金属原子数:4金属晶体的堆积方式──铜型 堆积模型采纳这种堆积的典型代表配位数晶胞镁型MgZnTi12简单立方Po6钾型NaKFe8铜型CuAgAu12总结思考：4中模型单位体积容纳原子数大小关系？52%68%74%74%空间利用率 1.空间占有率等径球两种最密堆积具有相同的堆积密度，晶胞中圆球体积与晶胞体积之比称空间占有率，六方最密堆积（hcp）与立方最密堆积（ccp）空间占有率均为74.05％。 设圆半径为R，晶胞棱长为a，晶胞面对角线长                 则                 晶胞体积立方面心晶胞中含4个圆球，每个球体积为:立方最密堆积虽晶胞大小不同，每个晶胞中含球数不同。但计算得到空间占有率相同。 而体心立方堆积（bcp）则空间占有率低一些。体对角线长为晶胞体积体心立方晶胞含2个球 2、某些金属晶体(Cu、Ag、Au)的原子按面心立方的形式紧密堆积，即在晶体结构中可以划出一块正立方体的结构单元，金属原子处于正立方体的八个顶点和六个侧面上，试计算这类金属晶体中原子的空间利用率。 2）.立方面心结构立方面心结构的配位数＝12（即每个圆球有12个最近的邻居，同一层有六个，上一层三个，下一层三个）。立方密堆积中可以取出一个立方面心的单位来，每个单位中有四个圆球，球心的位置是000；01/21/2；1/201/2；1/21/20。等径圆球的最紧密堆积方式，在维持每个球的周围的情况等同的条件下，就只有上述两种，它们的空间利用率最高（74．05％）。 立方体边长=a"；立方体对角线＝        a"；四面体边长=        a"； 金属晶体的原子堆积模型第二课时金属晶体 金属晶体的原子堆积模型（1）几个概念紧密堆积：微粒之间的作用力使微粒间尽可能的相互接近，使它们占有最小的空间配位数：在晶体中与每个微粒紧密相邻的微粒个数空间利用率：晶体的空间被微粒占满的体积百分数，用它来表示紧密堆积的程度 思考:1.如果把金属晶体中的原子看成直径相等的球体,把他们放置在平面上,有几种方式?2.上述两种方式中,与一个原子紧邻的原子数(配位数)分别是多少?哪一种放置方式对空间的利用率较高?行列对齐四球一空行列相错三球一空(最紧密排列)密置层(非最紧密排列)非密置层 （3）金属晶体的原子在三维空间堆积模型①简单立方堆积（Po） 简单立方堆积 ②体心立方堆积—钾型（碱金属） 体心立方堆积配位数：8 镁型铜型③镁型和铜型 123456第二层对第一层来讲最紧密的堆积方式是将球对准1，3，5位。(或对准2，4，6位，其情形是一样的)123456AB，关键是第三层，对第一、二层来说，第三层可以有两种最紧密的堆积方式。 第一种是将球对准第一层的球。123456于是每两层形成一个周期，即ABAB堆积方式，形成六方紧密堆积。配位数12。(同层6，上下层各3)，空间利用率为74% 下图是此种六方紧密堆积的前视图ABABA123456 3.镁型 第三层的另一种排列方式，是将球对准第一层的2，4，6位，不同于AB两层的位置，这是C层。123456123456123456 123456此种立方紧密堆积的前视图ABCAABC第四层再排A，于是形成ABCABC三层一个周期。得到面心立方堆积。配位数12。(同层6，上下层各3) ④面心立方:铜型BCA 堆积模型采纳这种堆积的典型代表空间利用率配位数晶胞简单立方Po(钋)52%6钾型(bcp)K、Na、Fe68%8镁型(hcp)Mg、Zn、Ti74%12铜型(ccp)Cu,Ag,Au74%12 1．下列有关金属元素特征的叙述中正确的是A．金属元素的原子只有还原性，离子只有氧化性B．金属元素在化合物中一定显正价C．金属元素在不同化合物中的化合价均不同D．金属单质的熔点总是高于分子晶体能力训练 2.某些金属晶体(Cu、Ag、Au)的原子按面心立方的形式紧密堆积，即在晶体结构中可以划出一块正立方体的结构单元，金属原子处于正立方体的八个顶点和六个侧面上，试计算这类金属晶体中原子的空间利用率。 3.已知金属铜为面心立方晶体，如图所示，铜的相对原子质量为63.54，密度为8.936g/cm3，试求（1）图中正方形边长a，（2）铜的金属半径raarrorr提示：数出面心立方中的铜的个数： 小结：三种晶体类型与性质的比较晶体类型原子晶体分子晶体金属晶体概念相邻原子之间以共价键相结合而成具有空间网状结构的晶体分子间以范德华力相结合而成的晶体通过金属键形成的晶体作用力共价键范德华力金属键构成微粒原子分子金属阳离子和自由电子物理性质熔沸点很高很低差别较大硬度很大很小差别较大导电性无（硅为半导体）无导体实例金刚石、二氧化硅、晶体硅、碳化硅Ar、S等Au、Fe、Cu、钢铁等 周期性结构的数学抽象表示点阵（格子）晶体结构=基元+点阵点阵←格矢（基矢）R=l1a1+l2a2+l3a3基矢←基元原胞（最小的基元）晶胞，配位数，密堆积晶体结构的特征周期性 复杂结构（基元中包含一个以上的原子） a1a3a2复杂结构的任何原子位置=格矢+原胞内位矢 原子在晶体中的平衡位置，相应于体系能量最低的位置，尽可能地紧密排列那么，如何排列同样大小的球，使空隙最小？——古老的Kepler堆积问题(1611)原子在晶体中如何排列？ 注意：原子平均占有的体积！UpDown六角密排立方密排密堆积 ca1a2a3思考：是否B格子？a六角密堆积－Hexagonalclose-packed(hcp) ABABABc/a=?caAAB六角密堆积hcp CABABCABCfcc（立方密堆）c/a=? fcc：每个晶胞共4个原子顶角原子：共8个原子，每个顶角原子8个晶胞共享，相当于每个晶胞1个顶角原子面上原子：共6个原子，每个面上原子2个晶胞共享，相当于每个晶胞3个原子堆积比：硬球体积与整个体积之比a堆积比（fcc结构） 堆积比 最近邻：离某一粒子最近的粒子，称为该粒子的最近邻配位数：最近邻的粒子数，描写粒子排列紧密的程度最大配位数=12（密堆积）：每个原子与同层六个原子相切；上下两层各与三个原子相切由于对称性关系，不可能有11，10，9，7，5的配位数配位数依次是12；8；6；4；3；2书中将配位数表述成格点最近邻的格点的数目配位数 简立方体心立方面心立方氯化铯（CsCl）氯化钠体积和配位数(举例) V=a3配位数：?简立方6 V=？配位数：？8a3/2原胞？体心立方 V=？配位数：？12a3/4原胞？面心立方 scPo(钋)fccAl,Cu,Ag,Au,Pt(铂),Pd(钯),bccLi,Na,Fe,Ca,WStructures:sc,fcc,bccOrdinarymetal bcc?CsCl结构(0,0,0)a/2(1,1,1)ClCs两个简立方套构而成 不同原子，配位数？绿球不相切时是不是稳定？求绿球相切时的半径比相切时，a=2R(a为边长)如果r>0.73R，稳定如果r<0.73R，不稳定1>r/R>0.73：氯化铯结构氯化铯结构 (0,0,0)a/2(1,0,0)V=a3/444a311SodiumChlorideStructure(NaCl结构)bcc?两套面心立方套构而成 0.73>r/R>0.41：氯化钠结构配位数？氯化钠结构大球有可能不切！6都相切时的半径比? NaClLiFKClAgFMgOMgSCaOCsClCsClCsBrCsITiClTuBrStructures:NaCl,CsCl两套面心立方沿晶轴套构而成两套简单立方沿体对角线套构而成 闪锌矿结构金刚石结构六角密堆积结构纤锌矿结构石墨C60及其生成物其他重要的结构 (0,0,0)a/4(1,1,1)V=a3/444a311配位数=？两个面心立方沿体对角线套构而成闪锌矿结构（立方ZnS）4 109.8oZnS结构 配位数=？类闪锌矿结构，但是同种原子Diamond(金刚石)结构4(0,0,0)a/4(1,1,1)两个面心立方沿体对角线套构而成 DiamondDiamondSiGea-SnZnSIII-V:GaAs,ZnSII-VI:HgSe,CdTeCuFAgI金刚石，闪锌矿结构 配位数：？12caHexagonalclose-packed(hcp)六角密堆积堆积比=? Crystalsc/aHe1.633Be1.581Mg1.623Ti1.586Crystalsc/aZn1.861Co1.622Cd1.996Zr1.594Idealc/a=1.633Structures:hcp 层间距3.35A，层与层之间弱VanderWaals力石墨 Kroto,Smalley,Curl在1985年研究星际尘埃时意外发现结构？想象力！直觉！圆穹顶！足球！12个五边型，20个六边型组成的平截二十面体1989年，Huffman大量制备，证实足球状分子（实际上1983年曾发现）直径约7埃五边型键长1.46A，六边型相邻双键长1.39A1996年获Nobel化学奖！C60 对于人类的进步，直觉有时比知识更重要。因为知识是有限的，而正确的直觉却是永恒的！——AlbertEinstein 复杂结构密堆积，堆积比，配位数一些重要的晶体结构小结 调治脾胃用药特点与治疗方法 抛砖引玉，贻笑大方。 脾胃学说是祖国传统医学理论的一个重要组成部分，它不仅阐明了脾胃的生理机能、病理机制，而且为临床辨证论治规律等方面提供了重要的理论和实践依据。脾胃学说的理论内涵博大精深，对整个中医药学理论的发展起到了极大的推动作用，经过长期的发展，逐渐成为独树一帜的学术流派。研究脾胃学术的发展历史、学术特点、临床运用与实验研究情况，从而更好的指导临床工作。 脾胃学说认为脾胃是人体“后天之本”，气血生化之源；脾胃位于中焦，是人体气机升降之枢纽；“脾胃内伤，百病由生”，脾胃既是内伤病发生的根本内因，又是外感病发生的内在因素。 临床上根据“治脾胃即所以安五脏”之理论，勿忘立足于调治脾胃。临床实践也证明，认真钻研中医理论，探求与灵活运用脾胃学说。 根据辨证施治“异病同治”的原则，针对很多疾病在疾病发生、发展的不同阶段出现脾胃为主的证候，此时，就可以依据脾胃理论，应用相应调理脾胃的方法治疗而取得明显的疗效。在大多数疾病的治疗中调理脾胃确是临床治疗的极其重要法则，可以取得良好的临床疗效，具有广泛的实用价值。 遵循《内经》“谨察阴阳之所在，以平为期。”的理论指导，根据脾胃学的基本理论，据理以立法，缘法以尽变，以达到“阴平阳秘”之目的。 一、调理脾胃的用药特点：1、注重健运、消补同用：脾胃为后天之本，古人云：“谷气者，比如国家之饷道也，……脾胃一败，则百药难效。”调治脾胃，重在恢复其纳化功能，纳化正常，则气血生化有源，正气充足，元气不断得到补充，“四季脾旺不受邪”。而且服食的药物始可吸收，转输全身，发挥其治疗效应。如现代人肥胖、血脂异常者越来越多，往往要重用行气、消导的药物，此时佐以补气的药物，融和消补药物于一炉，以防耗气。 2、升降相依、斡旋气机：升降出入是人体生命的基本形式，《素问·六微旨大论》“非出入，则无以生长壮老已；非升降，则无以生长化收藏。”而脾胃位居中焦，处于气机升降的枢纽，与其它脏腑的关系尤为密切，如肺之肃降、肝之生发、心火下降、肾水上涵等，均有赖脾胃升降枢纽之斡旋，脾胃升降正常，则气机升降通畅，若脾胃升降失常则气机为之紊乱。 升降并用有两个方面的含义，一是脾主升，用升补药物时不要忘了使用沉降的药物，要注意加入行气降气的药物，如厚朴、枳实等。另外，加上少量风药可以增加升补的力量；二是脾升胃降，在补脾气的同时，要加入降胃气的药物；同时选用药物行而不燥，并具有和胃清热解郁的作用。 3、润燥相济、阴阳平衡：脾喜燥而恶湿，胃喜润而恶燥，胃燥太过，阴液必伤；脾湿太过，则为生痰化饮，在临床用药时要注意燥湿而不伤阴，养阴而不碍湿，这样才能使脾胃功能协调，促进疾病康复。养阴不碍祛邪，燥湿不可伤阴；养阴不用滋腻之品，如太子参、麦冬、南北沙参、玉竹、女贞子，一般不用生地或熟地；燥湿化湿一般用藿梗、荷叶，不用温燥之品。 4、虚实同调、扶正祛邪：脾胃之病常常虚实夹杂，脾胃虚弱兼有痰饮、瘀血、气滞、便秘、食停。目前城市人所患疾病主要与生活方式有关，特别是与饮食生活不规律、冷热不调、饥饱不节有关，出现纯虚纯实、纯寒纯热者很少，往往是湿、浊、痰、郁、瘀互现，内伤外感皆有，寒热兼夹，食滞与脾虚共存，上下同病，所以要要圆机活法，要将诸法融为一炉。虚实同调，补虚不忘治实，治实不忘补虚，补虚不要峻补，治实不要孟浪，掌握二者的轻重缓急，所以在临床上多用平补、淡补的药物，如太子参、南沙参、北沙参、茯苓、炒薏苡仁、山药、茯苓。 5、互为表里、脾胃并重：脾胃经脉相连，功能相依，临床上应当脾胃并治，理脾不忘调胃，调胃不忘理脾，脾胃并治。 6、气血兼顾、走守协调：脾胃为气血生化之源，脾胃为多气多血之脏腑，“脾统血”、“脾裹血”。脾胃之病往往波及气血，形成气血同病。 二、具体治疗方法：治疗时始终以顾护脾胃生机为第一要义，要切中病机，全面统筹，运筹中州，脾胃同调，升降并用，纳化并施，润燥兼顾，上下合一，内外同治，缜密周到，方能万全；而且处方用药剂量不能大，贵在轻灵活泼，才能有利于药物和食物的吸收，提高疗效，促进恢复脾胃功能。 切忌过量，因其伤胃反而增加脾胃负担！ 1、调和营卫法“脾为之卫”，脾虚时可导致免疫功能低下。《内经》云：“阴者藏精而起亟，阳者卫外而为固。”调和营卫则脾胃健运，阴裕阳充，抵抗力自然提高，此法常用于表虚易感者。《金匮要略》治“虚劳里急诸不足”者黄芪建中汤。 2、健脾解表法本法常用于病久脾虚，卫外不固，易感风寒，舌淡，苔薄，脉细弱。用桂枝汤或四君子汤。临证体会前人总结桂枝汤“外证得之解表和营卫，内证得之化气调阴阳”临证运用确实如此。 3、补气健脾法本法常用于脾气亏虚或脾气不足或中气不足，脾不建运之证。腹胀便溏，食欲不振，脘腹痞满，神疲乏力，少气懒言，舌淡，苔薄，脉细弱。李乾构老师选用六君子汤合玉屏风散疗效肯定。 4、健脾化痰法本法常用于脾不建运，痰浊内生之证。头昏头重，脘腹痞满，神疲乏力，眩晕，呕恶等症，舌淡，苔白腻，脉沉滑。丹溪云：“无痰不作眩。”脾失健运，痰浊内生，若夹肝风内动，出现头重头晕、目眩欲倒、恶心作呕，选用东垣半夏白术天麻汤。可用此法治疗中风后遗症偏瘫，纳差，眩晕，多痰者取效明显。 5、健脾除湿法本法常用于脾虚湿困，湿困脾阳，甚或脾肾虚弱，水饮内停之证。大便稀溏，脘腹痞满，食欲不振，神疲乏力，肢体沉重，甚至水肿，舌淡，苔白，脉沉濡缓。脾喜燥而恶湿，脾虚气弱则湿聚，聚于内则为痰为饮，泛于外则为肿为胀。其病机则与脾肺肾三脏关系最为密切。故张景岳说：“水为至阴，故其本在肾；水化于气，故其标在肺；水惟畏土，故其制在脾。”所以，健脾利湿是治水的主要环节，也是开鬼门洁净府的关键所在。《金匮要略》“病痰饮者当以温药和之”为其治则。治以健脾利水；偏于脾阳虚，选用参苓白术散；偏于肾阳虚，选用实脾饮。 6、甘温除热法本法常用于内伤发热之证。多属脾胃虚弱，元气受伤，中焦虚寒，症见发热以下午、晚上明显，倦怠嗜卧，四肢不收。如果反复表散，则反而加重病情。“阴虚则生内热”，“阳气者烦劳则张”，此内伤发热之原理。甘温之剂能益脾胃之气，使阳生阴长，相互协调，则“阴平阳秘”，而虚热自除。东垣曰：“甘温能除大热。”尤在泾曰：“温之则浮焰自熄，养之则虚火自除，”即对此症而言也。所谓“劳者温之，损者益之”是也，选用补中益气汤。 7、健脾升陷法本法常用于脾失健运，升降失司，清不升浊不降之证。证见内脏下垂，面黄消瘦，腹部重坠，声低气短，脘腹痞满，食欲不振，神疲乏力，肢体沉重，舌淡齿痕，苔白，脉细无力。治以补益脾气，升提举陷，予补中益气汤合七味白术散加减。 8、升清降浊法《灵枢·本输篇》：“肺合大肠，大肠者，传导之府。”大便阻塞不通者，古人有开肺气的治法。叶天士于《临证指南医案》中“肠痹”一门，遵丹溪治肠痹，必开肺气，谓表里相应治法。亦《内经》所谓“肺主一身气化”，天气降，斯云雾清，而诸窍皆为通利，但“脾气散精，上归于肺”，又为肺气宣通之必具条件也。利用某些药物既可升又可降，在定向上存在二重性。从而达到戴裕光教授所说的“升清可以促进降浊，降浊又能促进升清”的目的，可选用验方升降汤。 9、心脾双补法用于心脾两虚，脾气虚弱，心神失养之证。心悸失眠，多梦，健忘胆怯，纳少腹胀，气短倦怠，月经失调，或崩漏，舌淡，苔白，脉细弱。治疗宜健脾益气，补心宁神，选用归脾汤。 10、疏肝和胃法用于肝气犯胃型，证见胃脘胀闷,，攻撑作痛,嗳气频作，每因情志剌激痛作或加重，或伴大便不畅。舌苔薄白或薄黄，脉沉弦或弦滑。治当疏肝理气、和胃降逆。“胃宜降则和”。肝胆气郁，多见胃气上逆，故降胃必须平肝。胃寒则泛清涎，胃热则食入即吐；过饱则宜消其食，过饥则宜填其空。和则纳，降则通，肝之疏泄利则气不滞血不瘀，而痛止矣。治疗选用柴胡疏肝散加减。 11、和胃利胆法胆邪犯胃，则痛呕胆汁，利胆而不和胃降逆，则非其治也。虽然，“十一脏皆取决于胆”，但调其升降者仍在脾胃，胆随胃降，故立和胃利胆法。胆附于肝，肝胆郁热，气滞血行不畅，故右上腹、胁下阵发性剧痛，呕吐黄水，小便黄，脉弦数。遵照《内经》所谓“疏其血气，令其调达，而致和平”，方用四逆散。 12、养胃安神法因情志抑郁，心脾受损，脏阴不足而设立养胃宁心法。《金匮要略》曰：“妇人脏躁，喜悲伤欲哭，象如神灵所作，数欠伸”。此法常用于脏躁证。方用甘麦大枣汤。 13、活血化瘀法用于胃痛瘀血之证。胃脘刺痛，痛处固定，疼痛拒按，痛时持久，甚至呕血黑便，食后痛甚，舌暗红，脉涩。选丹参饮、失笑散。如噎膈多属食管痉挛、狭窄、肿块等的临床表现。病位常见于食管的上、中、下段及贲门。症见食不得入或食入反出，伴吐涎沫，大便干燥如羊屎。病因多属忧郁、伤酒、过食咸菜等。病机属“津枯气结”瘀血阻滞，治可用养胃开结法，用通幽煎。 14、辛开苦降法湿热之气触自口鼻，若脾胃虚弱，内外相引，阻塞气分，三焦同病，湿则太阴，热则阳明，湿热郁蒸，常致清窍不灵，发热不退，此湿遏热伏，邪在卫分、气分，治宜清宣温化，化其浊，逐其秽。若湿重于热，肺气失宣，热蒸多汗，头昏头重，胸闷不饥，口渴不饮，便尿不爽，午后发热，状若阴虚，胸闷呕恶，饮食不入者，可与三仁汤加减；若热重于湿，神识昏朦，尿短黄赤者，与甘露消毒丹加减。 15、补土生金法本法常用于脾肺气虚，脾失建运，肺失宣降证。腹胀咳喘，纳少便溏，咳痰浮肿，胸闷气短，神疲自汗，舌淡，苔白，脉细弱。治疗宜健脾益气，补肺祛痰，方选补肺汤。 16、补脾生血法本法常用于出血后，生化不足，气血两虚之证。失血眩晕，面色无华，心悸气短，纳少化迟，神疲乏力，唇舌淡白，脉沉细弱。治疗宜补气健脾，生化气血，方选当归补血汤。 17、补脾摄血法本法常用于脾虚气弱、不能统血之证等。消瘦，面色苍白，食少腹胀，便溏倦怠，气短浮肿，皮下瘀斑色淡，舌淡齿痕，脉沉细弱。证属“虚斑”，系脾虚气弱不能统血，血随虚火游行，显于皮肤所致。应注意脾为后天之本。“温之则浮焰自息，养之则虚火自除”。脾气虚弱型，治补气以统血，宜归脾汤。杨仁斋《直指方》云：“一切血证，经久不愈，每每以脾胃药收功。” 18、健脾滋阴法本法常用于脾阴不足之证等。纳呆烦热，口咽干燥，手足心热，干呕呃逆，大便干结，舌红无苔，脉细数。治疗宜健脾助运，滋生脾阴，方选健脾滋阴汤（《万病回春》卷四）。 19、健脾疏肝法本法常用于肝脾不和，肝气抑郁，克犯脾土之证。胁痛腹胀，心烦易怒，胸腹痞满，脉弦。“见肝之病，……当先实脾。”“木郁则达之”，方选逍遥散。肝脾不和，肝阴不足，抑郁不舒，郁于上则胸胁隐痛，宜魏氏一贯煎(治在肝胃)；郁于下则小腹坠胀，宜逍遥散(治在肝脾)。中气虚弱，健运失司，以致水谷不化精微，聚湿生痰，痰浊交阻，引动肝风，则头晕眼花、视物旋转等症发作。治以健脾化痰，平肝熄风，则眩晕停而呕吐自止，治疗以半夏白术天麻汤。 20、消积导滞法用于饮食停滞之证，证见胃脘胀痛，嗳腐酸臭，或呕吐不消化食物，吐食或矢气后痛减，苔厚腻，脉滑。治当消食和胃、理气导滞，以保和丸或枳实导滞丸加减。 21、滋养胃阴法用于胃阴亏虚型，证见胃脘部灼热时痛，咽干口燥，或大便干结，或饥而不食，舌干少苔或无苔，呈镜面舌，脉细数。治当清胃滋阴、敛阴止痛，以叶氏养胃汤或益胃汤加减。 22、健脾和胃法用于脾胃气虚，脾胃不和之证。《明医指掌》云：“脾不和，则食不化；胃不和，则不思食。脾胃不和则不思而且不化。或吐，或泻，或胀满，或吞酸，或嗳气，或恶心，用治中汤。脾不和，不喜食而食不消者，枳实二陈汤、枳术丸；胃不和者，平胃散。”证见纳少腹胀，脘腹痞闷,不思饮食,恶心呕吐，面色萎黄或苍白，语音低微，气短身倦，四肢乏力,大便溏薄，舌淡边有齿印，苔薄白，脉虚弱或虚缓。治当益气补中、健脾和胃，选用参苓白术散加减。 23、化痰和胃法用于胆郁痰扰之证，证见胃脘痞满不适，烧心或隐痛，或嘈杂嗳气，心烦失眠，舌苔黄腻，脉弦数或滑数。治当清胆和胃、理气化痰，以温胆汤加减。 24、调和肝脾法用于肝旺脾虚之证，证见肠鸣腹痛，腹痛即泻，泻后痛缓，每因情志波动发作，矢气频作，舌淡红、苔薄白，脉弦。常见于肠易激综合症。治当抑肝扶脾、调中止泻，以痛泻要方合香连丸加减。 25、清热和胃法用于肝胃蕴热型，证见脘腹不适，泛酸嘈杂，嗳气时作，口苦口干，舌质红、苔黄腻，脉弦数。治当清热和胃，以泻黄散加减。 26、温运中阳法分温运脾阳和温通胃阳。脾阳虚则纳少腹胀，腹痛绵绵，喜温喜按，形寒气怯，四肢不温，或见肢体浮肿，小便短少，舌淡胖或有齿痕，苔白滑，脉沉迟无力。治法重在温运，方如香砂理中汤。 胃阳虚常见胃不思食，胃脘胀满，甚或作痛，或胃气不能下行反上逆而形成反胃呕吐，谷食不化，口淡无味，舌淡苔白，脉沉细或弦迟。治法重在温通，方如大建中汤。 27、通里攻下法分苦寒攻下和温里攻下。苦寒攻下多用于胃腑实积，痞满燥实坚或高热神昏，热结旁流，苔黄燥，脉实有力者。方选承气汤类方。温里攻下多用于阳虚寒实的留积证，方选温脾汤。 28、健脾温肾法本法常用于脾肾两虚之症。脾虚则湿聚，肾虚则水泛，故苓桂参术甘汤、附子理中汤温脾阳与肾阳；真武汤温肾阳与脾阳，此脾肾相关之正治法也。 29、益气宣窍法《素问·阴阳应象大论》“清阳出上窍”，各窍生理功能的正常发挥，有赖于脾胃清阳之性对它们的调节。反之，若清阳之性得不到舒展，则会出现清阳不升或清阳被遏诸症。清阳不升的主要病机是脾气虚弱，不能上升濡养清窍。《素问·玉机真脏论》曰“脾不及，则令人九窍不通。”《脾胃论·脾胃虚实论》亦日：“胃气一虚，耳目口鼻俱为之病。”因此，健脾补土、益气升阳是耳鼻喉科重要的治疗法则。选用补中益气汤、益气聪明汤或六君子汤。 30、清肠和胃法用于肠胃不和之证，证见脘腹胀满痞闷，干哕食臭，伴肠鸣下利，恶心呕吐，舌苔黄白相见或腻，脉弦或弦数。常见于溃疡性结肠炎。治当清热利湿、调和肠胃，以芍药汤或半夏泻心汤加减。 31、驱蛔安胃法用于湿热生虫，蛔虫扰胃之证。胃脘疼痛，时吐蛔，痛时鼓包，痛止如常，能食消瘦，唇面虫斑，嗜异物癖，苔白或黄，脉象多弦。治疗驱蛔杀虫，止痛安胃，方选乌梅丸。 32、和胃安眠法《素问·逆调论》云：“胃不和则卧不安。”予半夏秫米汤汤其卧立至，治疗脾胃功能失调引起的睡眠障碍。 脾胃学说是中医理论中的一颗璀璨明珠，调理脾胃是祖国医学治疗体系中一个重要的方面，《内经》曰“脾胃为后天之本”，“仓廪之官”,灌溉脏腑经络，四肢百骸；“脾胃内伤，百病由生。” 随着现代研究证实，在临床所见许多急慢性病中，如由脾胃有病而致他脏不安者，或由他之脏疾影响脾胃而以脾胃病证为主者，皆可从脾胃论治每多收效。它不仅能够治愈许多内科急慢性疾病，而且在临床各科范畴也得到广泛的运用。《景岳全书·论治脾胃》指出：“脾胃有病，自宜治脾。然脾为土脏，灌溉四旁，是以五脏中皆有脾气，……能治脾胃而使食进胃强，即所以安五脏也。”我们在临床上应该自觉依照“读经典，跟名师，做临床”的要求，遵循脾胃理论的指导，根据“治脾胃即所以安五脏”之理论，勿忘立足于调治脾胃，将脾胃学说广泛运用于临床实践中取得了良好的效果。 运用之妙，存乎一心。 不当之处，敬请指正。谢谢！'