最新4.3车桥解析课件PPT.ppt 26页

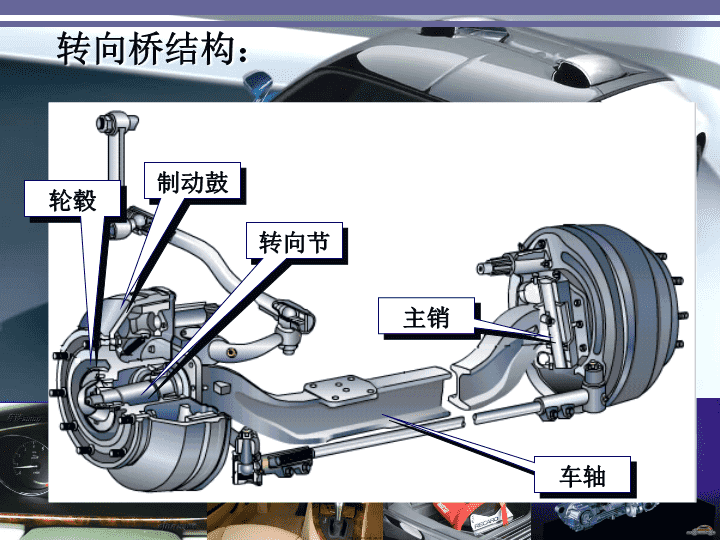
'4.3车桥解析 一、转向桥功用：①通过转向节使车轮可以偏转一定角度以实现汽车的转向；②承受一定的载荷。③应具有正确的定位角度与合适的转向角；性能要求：强度、刚度大；定位角、转向角正确；质量小。组成：前轴、转向节、主销、轮毂 转向桥结构：制动鼓转向节车轴主销轮毂 主销后倾作用：使转弯后的车轮自动回正，保持汽车直线行驶稳定性。γ<3°1、主销后倾装在前轴上的主销，上端向后倾斜的现象。 2、主销内倾装在前轴上的主销，上端略向内倾斜的现象。主销内倾角作用：1、使驾驶员转向操作轻便。 主销内倾角5～8°转向主销内倾角是指从车辆正面看在转向轮上转向主销轴线与铅垂直线的夹角β叫主销内倾角作用也是为了保持汽车直线行驶的稳定性。 3、前轮外倾作用：当车空载时，轮胎外缘与路面接触，当车载货时，在车重的作用下车轮垂直于路面，使轮胎能够均匀磨损。前轮外倾角 4、前轮前束汽车的前束角是汽车纵向中心平面与车轮中心平面和地面的交线之间的夹角。如果车轮的前部靠近汽车纵向中心平面，则前束为正值（前束角）；反之则为负值（后束角）。 车轮前束的作用消除汽车行驶过程中因前轮外倾而使两前轮前端向外张开的影响。一般前束值为0~12mm 作业：1、试述汽车行驶系的组成及功用？2、转向轮的定位参数有哪些？各起什么作用？ 标准2维表问题报告人：许细清学号：080320067报告时间：8/3/2021 问题描述设n是一个正整数。2×n的标准2维表是由正整数1，2，…，2n组成的2×n数组，该数组的每行从左到右递增，每列从上到下递增。2×n的标准2维表全体记为Tab(n)。 问题描述例如，当n=3时Tab(3)如下：123456124356125346134256135246任务:给定正整数n，计算Tab(n)中2*n的标准2维表的个数。 在解这道题之前，我想跟大家介绍下catalan(卡特朗数)，以及什么情况下的组合问题求解是卡特朗数。问题求解0(0,0）0’(0,0）A(n,n）A’(n,n）左图中，求从原点（0，0）到（n,n)点的路径数，要求中途所经过的点(a,b)满足关系a<=b; 问题求解0(0,0）A(n,n）从原点(0,0)到（n,n)点,总共走2n步，我们令往X轴走一步用0表示，往Y轴走一步用1表示，则从原点(0,0)到（n,n)的一条路径对应着有n个0和n个1组成的一个组合。问题要求a<=b;问题导致求从(0,0)出发，途径对角线0A及对角线上方的点到达（n,n)点的路径数。则可以途径0A上的点，但不允许穿越对角线（即对这2n个01序列，任何时候从左往右扫描，1的累计数不少于0的累计数。） 问题求解0(0,0）0’(0,0）A(n,n）A’(n,n）1.从0点出发经过0A及0A上方达到A点的路径对应着一条从O’点出发经过O’A’上方的点到达A’点的路径。2.从O’点出发途径0A上的点到达A‘点的路径，即为从O’点出发穿越O’A’到达A’点的路径，故对应一条从O点出发穿越OA到达A点的路径。3.所以，从O点出发经过OA及OA以上的点最后到达A点的路径数，等于从O’点出发到达A’点的所有路径数，减去从O’点出发路径OA上的点到达A’点的路径数。 问题求解O(0,0)(1,0)O’(0,1)A’(n,n+1）如左图,若点(0,1)到(n,n+1)点的某一条路径与y=x的交点从左到右依次p1,p2…pk,设Pk是最后一个在y=x上过的格子点,作(1,0)点到Pk点的一条道路(虚线),使之与上述的从(0,1)点到pk电脑的路径(实线)关于y=x对称.于是对从(1,0)点路经y=x这条直线到(n,n+1)点的一条路径对应从(1,0)到(n,n+1)的一条路径.结论:从（0，1）点到（n，n）点的路径数=从（1，0）点到（n,n）的路径数=C(2n,n+1);y=xP1A(n,n）P2PK 问题求解这个就是catala的公式，它对应的模型是：对于一个2n个有01组成的序列，从左向右扫描的话，0的累计数不小于1的累计数。 问题求解现在我们在重新看Tab这道题：题目要求把1到2n这2n个数放在一个2维表里，使得行值递增的，列值也是递增的。我们依次把1到2n这2n个数放进二维表里。由于要求行值递增&&列值递增，所以第一行的数肯定不小于第二行的数。证明如下：1.把1到2n这2n个数依次放进二维表时，每次放的位置一定是在第一行的行尾或第二行的行尾。不然中间将留有空白的地方。135245 问题求解第一行的个数一定要不小于第二行的数。如若不然的话，也会出现第一行存在空白。比如会出现以下情况。1368…24579…基于第一行的个数一定不小于第二行的个数，我们可以对Tab问题做投影。即：对这2n个数，如果放在第一行的我们设为0，放在第二行的我们设为1，则对于一个正确的Tab表的话，对应着一个2n个数的01序列，其中0的累计数不小于1的累计数。则Tab问题转化为这样的2n序列的个数。 问题求解123456124356125346134256135246000111001011010011010101001101我们之前已经分析过对于2n个有01组成的序列，其中从左到右扫面的话，0的个数不小于的1的个数的组合数为catalan数。所以: 问题求解由于组合数当n很大时乘积会超过int的范围，所以解这道题还需要涉及到大整数乘法。具体的大整数乘法这里不叙述了。大家可以看标准输出输出里面有一个优秀算法ppt报告模板。里面的内容就是介绍大整数乘法的。 谢谢！Thanksforyouattention！如果有何不对的地方，欢迎大家指正批评！'