最新一维小波matlab命令解读课件PPT.ppt 32页

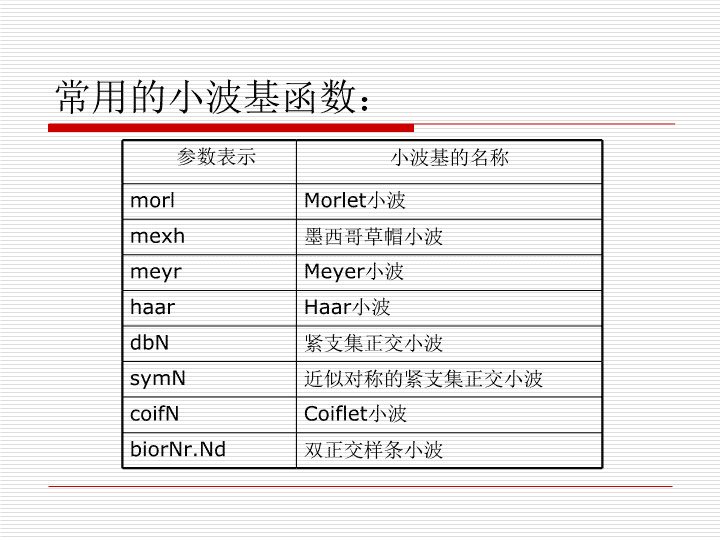
'一维小波matlab命令解读 常用的小波基函数：参数表示小波基的名称morlMorlet小波mexh墨西哥草帽小波meyrMeyer小波haarHaar小波dbN紧支集正交小波symN近似对称的紧支集正交小波coifNCoiflet小波biorNr.Nd双正交样条小波 怎样获取小波基的信息：在Matlab窗口键入“waveinfo(‘参数名’）?waveinfo("meyr")MEYRINFOInformationonMeyerwavelet.MeyerWaveletGeneralcharacteristics:Infinitelyregularorthogonalwavelet.FamilyMeyerShortnamemeyr 一维离散小波变换：单层分解[cA，cD]=dwt(X，’wname’)[cA，cD]=dwt(X，Lo_R，Hi_R)其中：cA：低频分量，cD：高频分量X：输入信号。wname：小波基名称Lo_R：低通滤波器Hi_R：高通滤波器 一维离散小波变换：单层重构X=idwt(cA，cD，’wname’)用’wname’小波把近似系数cA和细节系数cD重建原始信号X=idwt(cA，cD，Lo_R，Hi_R) 一维离散小波变换：单层重构X=idwt(cA，cD，’wname’，L)用’wname’小波把近似系数cA和细节系数cD重建信号中间长度为L的部分X=idwt(cA，cD，Lo_R，Hi_R，L) FWT(快速小波变换)：多层次分解[C，L]=wavedec(X，N，’wname’)[C，L]=wavedec(X，N，Lo_R，Hi_R)其中：C：各层分量，L：各层分量长度N：分解层数X：输入信号。wname：小波基名称Lo_R：低通滤波器Hi_R：高通滤波器 FWT(快速小波变换)：多层次分解D=detcoef(C，L，N)从分解系数[C，L]提取第N层细节系数D=detcoef(C，L)从分解系数[C，L]提取最后一层细节系数 FWT(快速小波变换)：多层次分解A=appcoef(C,L,’wname’,N)用’wname’小波从分解系数[C,L]提取第N层近似系数A=appcoef(C，L，Lo_R，Hi_R，N) FWT(快速小波变换)：多层次分解A=appcoef(C,L,’wname’)用’wname’小波从分解系数[C,L]提取最后一层近似系数A=appcoef(C，L，Lo_R，Hi_R) 例子：Loadnoissin%读入白噪信号S=noissin(1:1000);%取信号的前1000个采样点[c,l]=wavedec(s,3,‘db4");%对信号做层数为3的多尺度分解[cd1,cd2,cd3]=detcoef(c,l,[1,2,3]);%得到尺度3的近似系数ca3=appcoef(c,l,’db4’,3); 例子subplot(511);plot(1:1000,s);title(‘s")Subplot(512);plot(1:l(1),ca3);title(‘ca3");Subplot(513);plot(1:l(2),cd3);title(‘cd3");%1(i)存放的是相应参数的长度Subplot(514);plot(1:l(3),cd2);title(‘cd2");Subplot(515);plot(1:l(4),cd1);title(‘cd1");%将原始信号和分解后得到的一组近似信号和3组细节信号的波形显示出来。 FWT(快速小波变换)：多层次重构X=waveerec(C，L，’wname’)用’wname’小波对分解系数[C,L]进行一维小波重构。X=waverec(C，L，Lo_R,Hi_R) 例子：Loadnoissin%读入白噪信号S=noissin(1:1000);%取信号的前1000个采样点[c,l]=wavedec(s,3,‘db4’);%对信号做层数为3的多尺度分解rs=waverec(c,l,‘db4’);%对信号进行重构 例子subplot(211);plot(s);title(‘原始讯号’)Subplot(212);plot(rs);title(‘重构信号’);%将原始信号和重构信号的波形显示出来。 FWT(快速小波变换)：单尺度重构[NC,NK,cA]=upwlev(C,L,’wname’)用’wname’小波对分解系数[C,L]进行单尺度重构，返回上一尺度的分解结构[NC,NL]并提取最后一尺度的分解结构。[NC,NK,cA]=upwlev(C,L,Lo_R,Hi_R) 例子：Loadsumsin%读入信号s=sumsin(1:1000);%取信号的前1000个采样点[c,l]=wavedec(s,3,‘db1’);%对信号做层数为3的多尺度分解[nc,nl]=upwlev(c,l,‘db1’);%对信号进行重构，得到尺度2的小波分解结构 例子subplot(311);plot(s);title(‘原始讯号’)Subplot(312);plot(c);title(‘尺度3的小波分解结构’);Subplot(313);plot(nc);title(‘尺度2的小波分解结构’); FWT(快速小波变换)：对小波系数进行重构X=wrcoef(‘type’,C,L,’wname’,N)用’wname’小波对分解系数[C,L]进行重构，当type=a时，指对信号的低频部分进行重构。这时N可以为零。当type=d时，指对信号的高频部分进行重构。这时N为正整数。X=wrcoef(‘type’,C,L,Lo_R,Hi_RN) 例子：Loadsumsin%读入信号s=sumsin(1:1000);%取信号的前1000个采样点[c,l]=wavedec(s,3,‘db3’);%对信号做层数为3的多尺度分解a3=wrcoef(‘a’,c,l,‘db3’,3);%对尺度3上的低频信号进行重构 例子subplot(211);plot(s);title(‘原始信号’)Subplot(212);plot(a3);title(‘重构信号’); 科学管理理论对现代企业管理的借鉴 目录“科学管理之父”泰罗与科学管理理论科学管理理论的深远意义现代企业管理内容科学管理理论对现代企业管理的影响总结 泰罗与科学管理理论科学管理理论的创始人背景：资本主义经济高速发展，企业规模迅速扩大根本内容和目标：提高企业效率 科学管理理论的深远意义现代管理方法的起源科学管理思想的特点实践性科学性规范性协调性 现代企业管理内容涵盖内容生产作业管理、战略管理、人力资源管理、市场营销管理、财务管理、后勤行政管理、法律法规和企业文化等现代企业管理的发展动向组织结构扁平化管理方式的柔性化办公方式的分散化 科学管理理论对现代企业管理的影响科学管理思想对我国现阶段经济发展意义借鉴泰罗的科学管理思想,必须做到“五个结合”学习借鉴与革新创造相结合制度管理与思想教育相结合物质激励与精神激励相合管理者与工人相结合经济效益与社会效益相结合 总结学习泰罗的科学管理理论了解我国现阶段的企业发展目标和方向借鉴先进的管理理论思想提升企业现代化管理水平 谢谢大家！'