最新大学物理振动波动课件课件PPT.ppt 57页

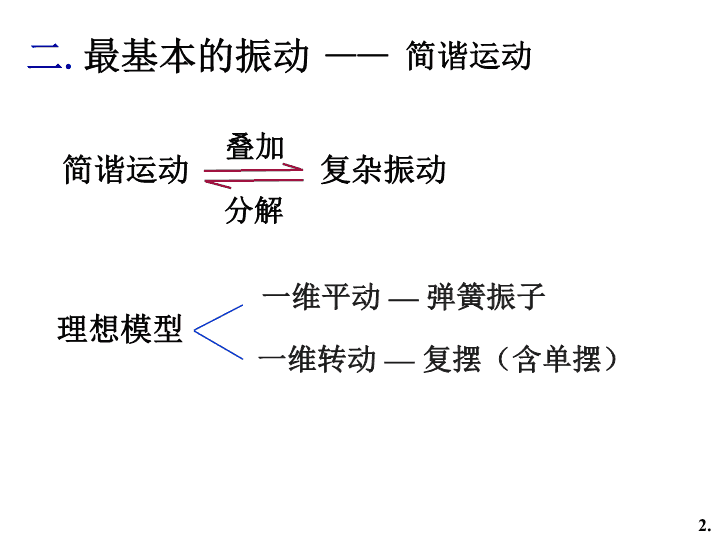
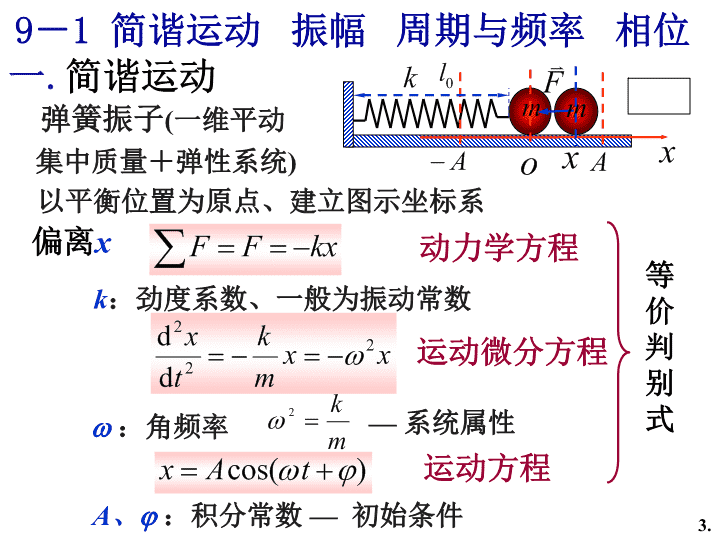
'大学物理振动波动课件 二.最基本的振动——简谐运动简谐运动复杂振动叠加分解理想模型一维平动—弹簧振子一维转动—复摆（含单摆）2. 9－1简谐运动振幅周期与频率相位一.简谐运动以平衡位置为原点、建立图示坐标系偏离x弹簧振子(一维平动集中质量＋弹性系统)k：劲度系数、一般为振动常数：角频率—系统属性A、：积分常数—初始条件动力学方程运动微分方程运动方程等价判别式3. 3.相位由前知xva—t时状态(相)k=0,1,2,…x=A,v=0x=0,v<0x=－A,v=0x=0,v>0(或)一般取k=0描述±2k—重复性如t=0则—初始状态7. —任意角(4个象限)4.常数A的确定(解析法)、t=0再结合v0(>0、=0、<0)判断或8. 9－2旋转矢量一.简谐运动与匀速圆周运动如图所示旋转矢量oM9. 矢端M投影点P关系运动性质匀速率圆周运动简谐振动合与分角频率同上同上角速度(逆)t=0角位置t时角位置相位初相位(t＋)数值相等MoP10. 注b.旋矢图相位状态一一对应a.规定＋－Ⅰ、Ⅱ、Ⅲ象限正角，一般：Ⅳ象限负角二.旋转矢量法1.表示谐振动（三要素）oxPx0v02.描绘x－t曲线3.确定初相位(或相位)(几何法)11. oP由图知讨论:如振子P，t=0时处于下状态，求(1)(2);相位差(初相差)规定逆时针在前为超前4.相位差(同频率)—两振动“步调”对(a)图x2超前x1(2－1)≤(b)图x1超前x2/2或x2滞后x1/2ox12图(a)ox图(b)12. oo5.t或oP回到平衡位置(第一次)如振子由初始状态(x0=－A/2,v0<0)由旋矢图知由此与t可互求6.谐振动合成(9－5)如同相“步调一致”反相“步调相反”13. 三.谐振动的运动学分析1.已知运动方程→一系列物理量2.由已知条件→运动方程(确定三要素)→其它物理量[例1]一质量为0.01kg的物体作简谐运动，其振幅为0.08m,周期为4s,起始时刻物体在x=0.04m处,向ox轴负方向运动（如图）.试求:(1)t=1.0s时,物体所处的位置和所受的力；(2)由起始位置运动到x=-0.04m处所需要的最短时间.14. 分析:求(1)a.先求运动方程(三要素),其中为关键b.和t求解解析法旋转矢量法如:解析法由判断旋矢法由旋矢图知(2)x=0.04m到-0.04m最短时间15. 由图知[例2]一简谐运动的x–t曲线，如图所示，求：(1)初相；(2)求运动方程,并用旋矢表示之；(3)第一次到达处的速度和加速度。分析:a.简便路径:用旋矢法求和,并结合相位法求第三问b.旋矢图oP第一次到达次处相位比较：解析法、旋矢法、相位法讨论:116. 如(物理摆)—一维角谐振动模型OAm转动正向9－3单摆和复摆一.复摆运动方程(准谐振动)如图偏离平衡位置l—质心c至转轴o距离二.单摆(数学摆)—复摆一个特例*（C点为质心）CO转动正向有17. ORr[例1]一半径为r的均质球,可沿半径为R的固定大球壳的内表面作纯滚动(如图)试求圆球绕平衡位置作微小运动的动力学方程及其周期.分析:偏离力(矩)分析18.c [例2]细杆(m,l)竖直时,水平轻质弹簧(k)处于自然状态,求细杆作小幅摆动时的周期T。分析:偏离对o:LKoθ很小时,有讨论:动力学分析步骤?19. t:系统能量以弹簧振子为例9－4简谐运动的能量守恒4T2T43T能量势能动能总能量20. 简谐运动——能量特征——能量守恒讨论:能量法——判断广义简谐运动振子偏离平衡位置x时以弹簧振子为例：两边对t求导21. [例]求图示系统的振动频率.设轻绳与定滑轮间无相对滑动.xoxx0分析:a.寻找平衡位置,建立图示坐标系b.Ⅰ法动力学法偏离x平动与转动隔离对m:对J:m与J:对J:对m:——系统固有性质22. xoxx0偏离x系统(m、k、J、地球)c.Ⅱ法能量法两边对t求导，并考虑，，可得同样结果23. 9－5简谐运动的合成一.两个同方向同频率简谐运动的合成与相位差有关仍为谐振动，不变24. a.如讨论:b.如或如静止a.以上为两相干波干涉的基础注b.建议：对下列特殊情况可直接用旋矢法求解如(同相或反相),和对x或y轴对称,同相合成最强反相合成最弱25. [例]一谐振动分别与下列谐振动合成,求合运动方程.(1)(2)(3)(4)比较：旋矢法与解析法讨论:26. 合振动轨迹方程(消去t)——椭圆方程二.两个相互垂直同频率简谐运动的合成27. 讨论:a.所含各种情况=0,直线(谐振动)=/2,3/2正椭圆如A1=A2圆—其他情况斜椭圆b.右旋与左旋如=2-1>0如=2-1<0x超前y逆时针旋转(左旋)y超前x顺时针旋转(右旋)28. *三.多个同方向同频率简谐运动的合成如:相位差依次恒为合运动仍为简谐运动EGR如则29. 讨论:a.若b.若（N个矢量构成一闭合图形）如（如图）如（如图）同相合成最大30.c.次级大 四.两个同方向不同频率简谐运动合成—拍一般：合运动——不是谐振动讨论,的情况31. 合运动如随t变化的振幅振动因子可证明拍频——振幅变化的频率32. 比较证明(1)解析法证明(2)旋矢法从两振动同相—再次同相由相对运动拍现象应用领域—声学、无线电技术、速度测量33. 一.阻尼振动简谐运动—理想等幅守恒9－6阻尼振动受迫振动共振实际阻尼C为常数设如2<02其解为式中A,—初始条件↓202↓34. 讨论:临界阻尼——工程中有很多应用c.临界阻尼b.过阻尼a.欠阻尼35. 二.受迫振动周期性简谐外力则其解暂态响应稳态响应特征稳定后(谐振动),—多种因素有关(如0、P、)振动频率—驱动外力P机械能守恒36. 三.(位移)共振共振频率ω0*另速度共振—电流谐振(选频)令速度最大令共振—有弊也有利37. 一.振荡电路无阻尼自由电磁振荡LCS9－7电磁振荡LC电路(无阻尼情况)电荷与电流电场与磁场周期性转换L+C(a)L+C(c)LC(b)LC(d)I0I038. 二.无阻尼电磁振荡的振荡方程LC电路t:有振动周期广义简谐运动39. 三.无阻尼电磁振荡的能量t:电容器电感线圈总能量守恒40. *9－8简述非线性系统一.线性系统(理想或近似)特征1.动力学行为—满足(一组)线性微分方程2.其解—满足线性叠加原理3.由—精确描述动力学过程边界条件初始条件确定性二.非线性系统(实际,普遍)特征1.叠加原理不成立2.初始条件不同,会导致很不相同运动形式3.可能出现完全随机混沌行为41. 讨论:小角度(线性系统)和大角度(非线性系统)物理行为1.小角度摆(<5°)线性微分方程其解精确描述状态—确定性两同频率谐振动合成——满足线性叠加原理满足其解42. 非线性微分方程如取前两项一次迭代近似解：2.大角度摆(>5°)不满足线性叠加原理近似：两个不同频率谐振动合成（复杂振动）其中与A（能量，初始条件）有关43. 初始条件不同可能会导致下列三种不同运动—不确定性以上通常用如下相图(P-x或-或…)描述d/dt44. d/dt施加某种影响——完全随机行为——混沌满足某种条件（前沿课题）45. 第七节正弦定理和余弦定理掌握正弦定理、余弦定理；能解决一些简单的三角形度量问题. 基础回顾 3.三角形中常用的面积公式：4.正弦定理解决的问题：已知两边以及一边的对角；已知两角以及任意一边；两边以及夹角求三角形面积.余弦定理解决的问题：已知两边以及夹角；已知三边解三角形；已知两边及一边对角(解一元二次方程).基础回顾 考向一　利用正、余弦定理解三角形例1 反思感悟：应熟练掌握正、余弦定理及其变形．解三角形时，有时可用正弦定理，也可用余弦定理，应注意用哪一个定理更方便、简捷方法二： 1.在即时应用学会判断采用哪个定理更简单；注意隐含条件：三角形内角和定理. 例2考向二　利用正、余弦定理判断三角形形状 反思感悟：判断形状时候边化角或者角化边，转化为边边关系（因式分解）或者角的关系（三角函数恒等变形），注意：隐藏条件，不漏解. 即时应用B 例3考点四考向三　与三角形面积有关的问题 课堂总结　感悟提升'