最新大气辐射与遥感-第六章课件课件PPT.ppt 73页

'进入夏天，少不了一个热字当头，电扇空调陆续登场，每逢此时，总会想起那一把蒲扇。蒲扇，是记忆中的农村，夏季经常用的一件物品。　　记忆中的故乡，每逢进入夏天，集市上最常见的便是蒲扇、凉席，不论男女老少，个个手持一把，忽闪忽闪个不停，嘴里叨叨着“怎么这么热”，于是三五成群，聚在大树下，或站着，或随即坐在石头上，手持那把扇子，边唠嗑边乘凉。孩子们却在周围跑跑跳跳，热得满头大汗，不时听到“强子，别跑了，快来我给你扇扇”。孩子们才不听这一套，跑个没完，直到累气喘吁吁，这才一跑一踮地围过了，这时母亲总是，好似生气的样子，边扇边训，“你看热的，跑什么？”此时这把蒲扇，是那么凉快，那么的温馨幸福，有母亲的味道！　　蒲扇是中国传统工艺品，在我国已有三千年多年的历史。取材于棕榈树，制作简单，方便携带，且蒲扇的表面光滑，因而，古人常会在上面作画。古有棕扇、葵扇、蒲扇、蕉扇诸名，实即今日的蒲扇，江浙称之为芭蕉扇。六七十年代，人们最常用的就是这种，似圆非圆，轻巧又便宜的蒲扇。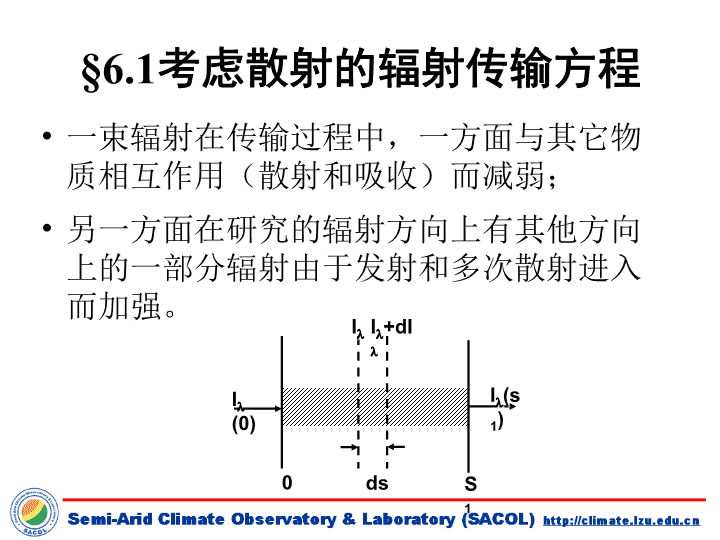　　蒲扇流传至今，我的记忆中，它跨越了半个世纪，也走过了我们的半个人生的轨迹，携带着特有的念想，一年年，一天天，流向长长的时间隧道，袅大气辐射与遥感-第六章课件 第六章行星大气辐射传输6.1考虑散射的辐射传输射传输方程(RTE)6.2散射相函数的展开6.3辐射传输方程解法6.3.1二流近似(two-stream)6.3.2逐次散射近似6.3.3离散纵标方法（DISORT）6.3.4加倍法6.3.5蒙特卡洛法(MonteCarlo) 一束辐射在传输过程中，一方面与其它物质相互作用（散射和吸收）而减弱；另一方面在研究的辐射方向上有其他方向上的一部分辐射由于发射和多次散射进入而加强。I(0)I(s1)I+dII0dsS1§6.1考虑散射的辐射传输方程 实际中，云、气溶胶粒子对短波乃至红外波段的散射效应都不能忽略，在一些情况下传输方程中必须考虑散射作用。上式中dIemit与dIscat是源函数。已知考虑基尔霍夫定律，根据普朗克函数可以表示dIemit，需要考虑dIscat的形式 对于dIscat的思考如果没有散射，即没有dIscat的贡献，因此散射项的贡献应该与散射系数βs的大小成正比；在任意方向上传输的辐射，都可能被散射到我们关注的某个方向上，从而对该方向的辐射强度有贡献；任意方向传输的辐射在某个方向上的散射贡献是以线性方式累积的。 dIscat的数学表示根据上述表示，dIscat可以表示如下：其中归一化的散射相函数为： 电磁波通过介质时，会发生散射，即电磁波有可能改变方向。因此使某一方向的电磁波强度发生变化，可能减弱，也可能增强。源函数中散射的表达 Ω0Ω单次散射多次散射当电磁波由方向Ω0传输时，它被介质散射到方向Ω的散射过程包括：单次散射和多次散射过程；单次散射过程指光子被介质只散射了一次，与单次散射相区别，凡是辐射被介质散射超过1次，均称为多次散射。区分单次散射和多次散射是为了方便于求解辐射传输方程。 根据互易原理：因此同样有：散射相函数（scatteringphasefunction）散射相函数P(Ω,Ω’)表述为方向Ω’的电磁波被散射到方向Ω的比例，且P(Ω,Ω’)/4π是归一化的，即： 通常散射相函数P(Ω,Ω’)只与方向Ω’和方向Ω之间的夹角Θ有关，可以写为P(cosΘ)。散射角Θ定义为入射光束和散射光束之间的夹角。散射角的余弦可以表示为： 对各向同性散射，g为零；当相函数的衍射峰变得越来越尖锐时，g也随之增大；若相函数峰值位于后向，g为负值；(1+g)/2可以看作积分前向散射能量的百分比数；(1-g)/2可以看作积分后向散射能量的百分比数。不对称因子g 实际上辐射被介质散射的同时，也被介质吸收，即消光过程既包括散射，也包括吸收。单次散射反射率ω定义为辐射传输发生每一次消光过程中，散射占的百分比。单次散射反射率（singlescatteringalbedo） 对于单次散射，我们假设入射辐射强度的初始值为I0，传播方向为Ω0，则它到达τ处的辐射强度为：Ω单次散射多次散射τ单次散射源函数Ωo 在τ处发生单次散射后，散射到方向Ω的辐射强度即为：对上式中入射方向Ω0在4π空间积分，并考虑只有一个入射方向，则上式中的强度变成通量密度，即有：上式就是单次散射产生的源函数。 则多次散射产生的源函数为来自所有方向、并经散射，到方向Ω的辐射总和。即上式对方向Ω’在4π空间的积分，即：对于多次散射，我们假设位于τ处、传播方向为Ω’的辐射强度为I(τ,Ω’)，则它散射到方向Ω的辐射强度为：多次散射源函数 源函数中的散射的表达是单次散射与多次散射之和，即：又，源函数中的发射的表达可以写为：普朗克函数B(T)是物体亮温为T时的出射辐射亮度，它的强度与方向无关，即各向均一。 因此，考虑散射（单次、多次）、发射源函数后，辐射传输方程可以展开为：通常情况下，这个方程没有解析解，只能靠数值解法或简化求解。对于平面平行介质中的传输方程为： 不考虑源函数、源函数与待求强度无关（只考虑发射或/和单次散射）、考虑多次散射，这三种情况的解由易到难。对多次散射的考虑，构成辐射传输求解中最具活力的一部分，相关新方法和手段层出不穷。辐射传输方程在不同介质中应用时，关键是要确定散射相函数P(Ω,Ω’)、τ、ω的形式，以及如何将它与介质的一些参数建立联系。 之前给出不考虑源函数J时传输方程的解(比尔定律），显然这是极不准确的。这里给出考虑源函数J（J与I无关）时传输方程的解。仍考虑平面平行介质，其传输方程为：，则得到J与I无关的传输方程解将方程两边同时乘以 对上式从0到τ0积分：整理得：位于τ=0处的强度由两部分组成：τ=τ0处辐射强度经整层介质衰减后的值；介质中的辐射源被衰减后到达τ=0处的强度总和。 位于τ=τ0处的辐射强度由两部分组成：τ=0处的辐射强度穿过整层介质衰减后的值；整层介质中的辐射源被衰减后到达τ=τ0处的辐射强度的总和。对同理，对于u<0时，有： 辐射传输方程的求解是对τ的积分，而J与I是否有关决定了求解难易；不考虑源函数的解为比尔-布格-朗伯定律，只考虑发射的解也相对简单；注意辐射传输方程中单次散射项也与I无关： 问题的关键：1.I在太阳方向上有峰值2.P(cosθ)存在峰值散射项引起的困难 6.2散射相函数的展开散射相函数是散射角的函数，可以展开为勒让德(Legendrepolynomial)多项式组成的级数:其中Pl为勒让德多项式，为展开系数： 当n=l时，当n≠l时，勒让德多项式勒让德多项式在-1≤x≤1,满足如下正交关系： 当l=0时，，P0=1,表明相函数是归一化的：当l=1时，P1=x,则有 其中表示由方向的入射辐射改变到方向的出射辐射。考虑到散射角与入射和出射方向的关系，相函数可以表示为: 根据球面调和函数的加法定理，散射相函数可展开为:为连带勒让德多项式。若m=0其他 近似方法:二流近似(two-stream)逐次散射近似Eddington近似精确方法：离散纵标法(Discrete-ordinates)累加法(Adding-doubling)最精确方法：蒙特卡洛方法(MonteCarlo)6.3辐射传输方程解法 6.3.1二流近似(two-stream)对于辐射传输方程(不考虑发射)，有：假定散射各向同性，辐射传输与方位φ无关，而仅与μ有关时，则有： 定义方位平均的强度：定义方位平均的相函数为：定义： 根据上述定义，向上、向下的辐射传输方程可写为：（1）（2） 分别将（1）、（2）式，对μ进行积分：（3）（4） 1.将相函数展为两项:2.用Gauss积分求和代替积分为了便于求解方程，给定两个简化条件： 将相函数展开为两项，并用两点Gauss求积公式计算传输方程，引用以下标记： 将则二流近似传输方程可表示为：二流近似的辐射传输方程是一阶非齐次常微分方程组，可以得到解析解，有兴趣者可以翻看相关参考资料。 利用二流近似方法可以求解多次散射影响，尤其适合于通量密度的解算。3个关键步骤：与方位无关时辐射传输方程的简化—去掉φ勒让德多项式展开：将μ与μ’分开高斯公式展开：将μ’积分换成求和 6.3.2逐次散射近似多次散射的逐次计算方法是这样一种方法，我们单独对散射一次、二次、三次等的光子计算其强度，而总强度则为所有各次散射之和。即式中n表示光子经过散射的次数。注意到多次散射的源函数为： 由于二次散射是由一次散射引起的，因而从一次散射强度I1(τ,Ω)即可求出二次散射源函数：而二次散射强度是可以由其源函数计算出来的： 同样我们可以由二次散射强度推导出三次散射源函数，继而推出三次散射强度。依此类推，我们可以得到任意次散射的强度，其递归关系式可以表示为： 在辐射传输方程中，单次散射源函数J与待求强度I无关，可以求出解析解。单次散射解中的第1项反映了比尔-布格-朗伯定律，有时也称为零次散射解，而将第2项，即对源函数的积分结果称为单次散射解。利用逐次计算方法可以依次得到各次散射的源函数和强度，进而求出考虑多次散射的方程解。 利用离散纵标方法可以将辐射传输方程中的散射相函数用勒让德多项式展开，并用2N个节点的高斯求和公式代替方程中的天顶角积分，进而将原有的积分微分方程转化为微分方程组，最终通过边界条件的代入，求解辐射在几个特定方向（由高斯点决定）上的解析解。这种方法的精度取决于多项式展开的次数，次数越多精确性越高，但也越复杂。6.3.3离散纵标方法（DISORT） 6.3.4加倍法加倍法的思想是：如果有两层气层，他们的反射率和透射率已知，则由该两层叠合的气层总的反射率和透射率可以通过计算两气层之间来回的反射而得到。设在μ0方向有单位入射辐射，第一层的反射率为R1，透射率为（包括直接透射率和漫射透射率）为T1，第二层相应的量为R2，T2，两层总透射率为T12，总反射率为R12，两层之间总的向下透射为D，向上反射为U R12表示两层总的反射率：T12表示两层总的透射率： D表示两层之间向下的透射率：U表示两层之间向上的反射率： R12和T12可由D和U表示引入则将T、D分成直接透射与漫射透射两部分，即： 则根据上述定义，假定透射与太阳光束有关，μ’=μ0,则有：漫射透射部分为： 同理得：对于T12漫射透射部分为，透射与太阳辐射无关部分定义为μ’=μ：上式最后一项说明，直接透射只与μ0有关 加倍法的思路：根据以上方程可知，当已知R1，R2和T1，T2后，T12和R12均可求出，也就是说要求任何气层的反射率和透射率，只要将气层多次等分，若已知最初薄层的T1和R1，则通过若干次加倍后便可得整个气层的R和T 根据辐射传输方程：若给定边界条件为：在此边界条件下的形式解为： 其中源函数J为：当气层很薄时，忽略J中多次散射项，并带入传输方程形式解中积分得： 则R1，T1分别为： 6.3.5蒙特卡洛法(MonteCarlo)蒙特卡洛方法是一种随机模拟方法。即将散射过程看作光子与介质随机碰撞的过程，而相函数就是散射到某一特定角度上的概率密度函数。通过对足够多光子的散射过程进行模拟，理论上就可以精确地确定辐射场。蒙特卡洛方法原理简单、灵活，是解算多次散射最精确的方法，可用于解决其他方法难以解决的各种问题，特别适合三维辐射传输问题，但该方法需要耗费大量机时。 蒙特卡洛方法并没有直接使用辐射传输方程，而是根据散射过程构造几个几率函数：首先给定一个在0-1均匀分布的随机函数RN：1.对于给定的光学厚度τ，消光系数βe，厚度为Z的介质，光子与介质发生作用前传输的距离s，则：判断光子是否透过介质，若没有透过介质则： 2.光子与介质发生碰撞后，吸收或者散射，随机产生一个数RN，若RN大于ω则表示被吸收，否则发生散射。3.若发生散射，则进一步判断散射的方向，分别产生两个随机数RN， 整个模拟过程可表述为：（1）设定气层厚度z，给出气层的消光系数βe；（2）在气层上边界θ0处进入一个光子；（3）取随机数RN，计算传输距离S，判定在铅直方向上光子的位置小于0或者大于Z。若光子已出上或下边界，则重新执行（2）；（4）取随机数RN，确定散射角，重复执行（3），并如此继续，直到发射足够多光子为止。 Monte-Carlo方法的特点：（1）无需对相函数做假定，适用于复杂的相函数；（2）对于平面平行或复杂形状的云块均可模拟，计算上没有差别，只需给出边界的形状即可；（3）由于是统计方法，结果误差与统计次数（发射的光子数）的平方根成反比，要得到比较精确的结果，须对大量光子进行统计。 人有了知识，就会具备各种分析能力，明辨是非的能力。所以我们要勤恳读书，广泛阅读，古人说“书中自有黄金屋。”通过阅读科技书籍，我们能丰富知识，培养逻辑思维能力；通过阅读文学作品，我们能提高文学鉴赏水平，培养文学情趣；通过阅读报刊，我们能增长见识，扩大自己的知识面。有许多书籍还能培养我们的道德情操，给我们巨大的精神力量，鼓舞我们前进。 第四章肺系疾病第五节反复呼吸道感染 第五节反复呼吸道感染概述:一、定义：感冒、扁桃体炎、支气管炎、肺炎等呼吸道感染性疾病是小儿常见病，若反复感染发病，单位时间内超过一定次数，即称为反复呼吸道感染。二、发病情况：①年龄:多见于6个月～6岁小儿，1～3岁幼儿更常见。②季节:以冬春气候变化剧烈时尤易反复不已，夏天有自然缓解的趋势，一般到学龄期前后明显好转。③预后：若反复呼吸道感染，治疗不当，容易发生咳喘、水肿、痹证等病证，严重影响小儿的生长发育与身心健康。三、讨论范围：近似古籍中的虚人感冒、体虚感冒。四、中医优势。 第五节反复呼吸道感染【病因病机】1．禀赋不足，体质柔弱--不耐邪侵，一感即病（先天，肾虚骨弱）。2．喂养不当，调护失宜--脾胃化生乏源，脏腑功能失健，脾肺气虚，易遭外邪侵袭。（后天喂养，肺脾两虚）3．少见风日，不耐风寒--不耐风寒，一感即病，病后易传变（后天活动，肌肤柔弱）。4．用药不当，损伤正气--正不胜邪，反复感邪不已（营卫失和）。5．正虚邪伏，遇感乃发--（伏邪为病）总之，小儿反复呼吸道感染多因正气不足，卫外不固而造成。 第五节反复呼吸道感染【临床诊断】诊断要点：（1）感染频率＜2岁小儿，10次以上，其中（下）3次以上；3～5岁小儿，8次以上，其中（下）2次以上；6～12岁小儿，7次以上，其中（下）2次以上。（2）间隔时间：上呼吸道感染第2次距第1次至少要间隔7天以上。 第五节反复呼吸道感染【辨证论治】一、辨证要点：重在察邪正消长变化感染期邪实为主—辨病邪、辨兼证；迁延期正虚邪恋—辨恋邪，辨脏腑；恢复期则以正虚为主—关键在正虚，辨脏腑。二、治疗原则：本节所述，以恢复期治疗为主，此时要抓住补益的时机，使“正气存内，邪不可干”，以达到减轻减少发作的效果。 第五节反复呼吸道感染三、证治分类1、营卫失和，邪毒留恋辨证--肺卫虚弱或治疗不当（过汗）+平时汗出多而不温，+邪毒留恋的表现（咽红扁桃体肿大不消，或肺炎喘嗽久不康复等）。治法--扶正固表，调和营卫。方药--黄芪桂枝五物汤加减（防感合剂）。 第五节反复呼吸道感染2、肺脾两虚，气血不足辨证—后天失调，喂养不当+肺虚（屡受外邪，咳喘迁延，多汗）脾虚（面黄少华，肌肉松弛，厌食便溏）。治法--健脾益气，补肺固表。方药--玉屏风散加味（抗感至宝合剂）。 第五节反复呼吸道感染3、肾虚骨弱，精血失充证候—先天禀赋不足或后于日照不足+生长发育迟缓，五迟证候。治法--补肾壮骨，填阴温阳。方药--补肾地黄丸加味。 第五节反复呼吸道感染其他疗法：一、中药成药：黄芪颗粒、玉屏风口服液、童康片、百令胶囊、还尔金(槐杞黄)颗粒等。二、针灸疗法：耳压法、捏脊、针四缝 第五节反复呼吸道感染三、西医治疗：1、维生素治疗：对于维生素缺乏症者，及时补充维生素A、D、C、B2、B6、E。2、微量元素治疗：对于伴有微量元素缺乏症者，应定时给于锌、铁、铜、锰等治疗。注意用药时间不宜过长。3、免疫调节剂：对于患有免疫缺陷或免疫功能低下者，应给予免疫调节剂。常用的药物有胸腺肽、重组细胞因子及细胞因子诱生剂（干扰素）、左旋咪唑、转移因子、丙种球蛋白、泛福素等。'