数据库系统概念全套配套课件PPT ch13.ppt 77页

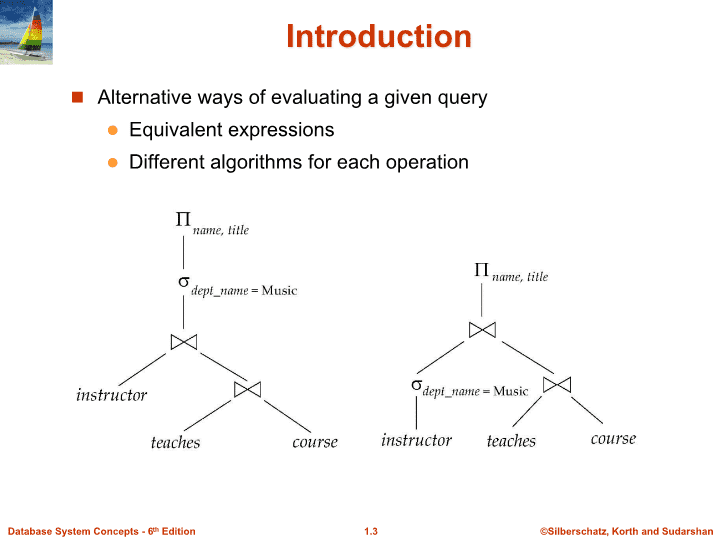
'Chapter13:QueryOptimization Chapter13:QueryOptimizationIntroductionTransformationofRelationalExpressionsCatalogInformationforCostEstimationStatisticalInformationforCostEstimationCost-basedoptimizationDynamicProgrammingforChoosingEvaluationPlansMaterializedviews IntroductionAlternativewaysofevaluatingagivenqueryEquivalentexpressionsDifferentalgorithmsforeachoperation Introduction(Cont.)Anevaluationplandefinesexactlywhatalgorithmisusedforeachoperation,andhowtheexecutionoftheoperationsiscoordinated.Findouthowtoviewqueryexecutionplansonyourfavoritedatabase Introduction(Cont.)CostdifferencebetweenevaluationplansforaquerycanbeenormousE.g.secondsvs.daysinsomecasesStepsincost-basedqueryoptimizationGeneratelogicallyequivalentexpressionsusingequivalencerulesAnnotateresultantexpressionstogetalternativequeryplansChoosethecheapestplanbasedonestimatedcostEstimationofplancostbasedon:Statisticalinformationaboutrelations.Examples:numberoftuples,numberofdistinctvaluesforanattributeStatisticsestimationforintermediateresultstocomputecostofcomplexexpressionsCostformulaeforalgorithms,computedusingstatistics GeneratingEquivalentExpressions TransformationofRelationalExpressionsTworelationalalgebraexpressionsaresaidtobeequivalentifthetwoexpressionsgeneratethesamesetoftuplesoneverylegaldatabaseinstanceNote:orderoftuplesisirrelevantwedon’tcareiftheygeneratedifferentresultsondatabasesthatviolateintegrityconstraintsInSQL,inputsandoutputsaremultisetsoftuplesTwoexpressionsinthemultisetversionoftherelationalalgebraaresaidtobeequivalentifthetwoexpressionsgeneratethesamemultisetoftuplesoneverylegaldatabaseinstance.AnequivalencerulesaysthatexpressionsoftwoformsareequivalentCanreplaceexpressionoffirstformbysecond,orviceversa EquivalenceRules1.Conjunctiveselectionoperationscanbedeconstructedintoasequenceofindividualselections.2.Selectionoperationsarecommutative.3.Onlythelastinasequenceofprojectionoperationsisneeded,theotherscanbeomitted.SelectionscanbecombinedwithCartesianproductsandthetajoins.(E1XE2)=E1E21(E12E2)=E112E2 EquivalenceRules(Cont.)5.Theta-joinoperations(andnaturaljoins)arecommutative.E1E2=E2E16.(a)Naturaljoinoperationsareassociative:(E1E2)E3=E1(E2E3)(b)Thetajoinsareassociativeinthefollowingmanner:(E11E2)23E3=E113(E22E3)where2involvesattributesfromonlyE2andE3. PictorialDepictionofEquivalenceRules EquivalenceRules(Cont.)7.Theselectionoperationdistributesoverthethetajoinoperationunderthefollowingtwoconditions:(a)Whenalltheattributesin0involveonlytheattributesofoneoftheexpressions(E1)beingjoined.0E1E2)=(0(E1))E2(b)When1involvesonlytheattributesofE1and2involvesonlytheattributesofE2.1E1E2)=(1(E1))((E2)) EquivalenceRules(Cont.)8.Theprojectionoperationdistributesoverthethetajoinoperationasfollows:(a)ifinvolvesonlyattributesfromL1L2:(b)ConsiderajoinE1E2.LetL1andL2besetsofattributesfromE1andE2,respectively.LetL3beattributesofE1thatareinvolvedinjoincondition,butarenotinL1L2,andletL4beattributesofE2thatareinvolvedinjoincondition,butarenotinL1L2.))(())(()(21212121EEEELLLLÕÕ=ÕÈqq)))(())((()(212142312121EEEELLLLLLLLÈÈÈÈÕÕÕ=Õqq EquivalenceRules(Cont.)ThesetoperationsunionandintersectionarecommutativeE1E2=E2E1E1E2=E2E1(setdifferenceisnotcommutative).Setunionandintersectionareassociative.(E1E2)E3=E1(E2E3)(E1E2)E3=E1(E2E3)Theselectionoperationdistributesover,and–.(E1–E2)=(E1)–(E2)andsimilarlyforandinplaceof–Also:(E1–E2)=(E1)–E2andsimilarlyforinplaceof–,butnotfor12.TheprojectionoperationdistributesoverunionL(E1E2)=(L(E1))(L(E2)) TransformationExample:PushingSelectionsQuery:FindthenamesofallinstructorsintheMusicdepartment,alongwiththetitlesofthecoursesthattheyteachname,title(dept_name=“Music”(instructor(teachescourse_id,title(course))))Transformationusingrule7a.name,title((dept_name=“Music”(instructor))(teachescourse_id,title(course)))Performingtheselectionasearlyaspossiblereducesthesizeoftherelationtobejoined. ExamplewithMultipleTransformationsQuery:FindthenamesofallinstructorsintheMusicdepartmentwhohavetaughtacoursein2009,alongwiththetitlesofthecoursesthattheytaughtname,title(dept_name=“Music”gear=2009(instructor(teachescourse_id,title(course))))Transformationusingjoinassociatively(Rule6a):name,title(dept_name=“Music”gear=2009((instructorteaches)course_id,title(course)))Secondformprovidesanopportunitytoapplythe“performselectionsearly”rule,resultinginthesubexpressiondept_name=“Music”(instructor)year=2009(teaches) MultipleTransformations(Cont.) TransformationExample:PushingProjectionsConsider:name,title(dept_name=“Music”(instructor)teaches)course_id,title(course))))Whenwecompute(dept_name=“Music”(instructorteaches)weobtainarelationwhoseschemais:(ID,name,dept_name,salary,course_id,sec_id,semester,year)Pushprojectionsusingequivalencerules8aand8b;eliminateunneededattributesfromintermediateresultstoget:name,title(name,course_id(dept_name=“Music”(instructor)teaches))course_id,title(course))))Performingtheprojectionasearlyaspossiblereducesthesizeoftherelationtobejoined. JoinOrderingExampleForallrelationsr1,r2,andr3,(r1r2)r3=r1(r2r3)(JoinAssociativity)Ifr2r3isquitelargeandr1r2issmall,wechoose(r1r2)r3sothatwecomputeandstoreasmallertemporaryrelation. JoinOrderingExample(Cont.)Considertheexpressionname,title(dept_name=“Music”(instructor)teaches)course_id,title(course))))Couldcomputeteachescourse_id,title(course)first,andjoinresultwithdept_name=“Music”(instructor)buttheresultofthefirstjoinislikelytobealargerelation.Onlyasmallfractionoftheuniversity’sinstructorsarelikelytobefromtheMusicdepartmentitisbettertocomputedept_name=“Music”(instructor)teachesfirst. EnumerationofEquivalentExpressionsQueryoptimizersuseequivalencerulestosystematicallygenerateexpressionsequivalenttothegivenexpressionCangenerateallequivalentexpressionsasfollows:RepeatapplyallapplicableequivalencerulesoneverysubexpressionofeveryequivalentexpressionfoundsofaraddnewlygeneratedexpressionstothesetofequivalentexpressionsUntilnonewequivalentexpressionsaregeneratedaboveTheaboveapproachisveryexpensiveinspaceandtimeTwoapproachesOptimizedplangenerationbasedontransformationrulesSpecialcaseapproachforquerieswithonlyselections,projectionsandjoins ImplementingTransformationBasedOptimizationSpacerequirementsreducedbysharingcommonsub-expressions:whenE1isgeneratedfromE2byanequivalencerule,usuallyonlythetoplevelofthetwoaredifferent,subtreesbelowarethesameandcanbesharedusingpointersE.g.whenapplyingjoincommutativitySamesub-expressionmaygetgeneratedmultipletimesDetectduplicatesub-expressionsandshareonecopyTimerequirementsarereducedbynotgeneratingallexpressionsDynamicprogrammingWewillstudyonlythespecialcaseofdynamicprogrammingforjoinorderoptimizationE1E2 CostEstimationCostofeachoperatorcomputerasdescribedinChapter12NeedstatisticsofinputrelationsE.g.numberoftuples,sizesoftuplesInputscanberesultsofsub-expressionsNeedtoestimatestatisticsofexpressionresultsTodoso,werequireadditionalstatisticsE.g.numberofdistinctvaluesforanattributeMoreoncostestimationlater ChoiceofEvaluationPlansMustconsidertheinteractionofevaluationtechniqueswhenchoosingevaluationplanschoosingthecheapestalgorithmforeachoperationindependentlymaynotyieldbestoverallalgorithm.E.g.merge-joinmaybecostlierthanhash-join,butmayprovideasortedoutputwhichreducesthecostforanouterlevelaggregation.nested-loopjoinmayprovideopportunityforpipeliningPracticalqueryoptimizersincorporateelementsofthefollowingtwobroadapproaches:1.Searchalltheplansandchoosethebestplaninacost-basedfashion.2.Usesheuristicstochooseaplan. Cost-BasedOptimizationConsiderfindingthebestjoin-orderforr1r2...rn.Thereare(2(n–1))!/(n–1)!differentjoinordersforaboveexpression.Withn=7,thenumberis665280,withn=10,thenumberisgreaterthan176billion!Noneedtogenerateallthejoinorders.Usingdynamicprogramming,theleast-costjoinorderforanysubsetof{r1,r2,...rn}iscomputedonlyonceandstoredforfutureuse. DynamicProgramminginOptimizationTofindbestjointreeforasetofnrelations:TofindbestplanforasetSofnrelations,considerallpossibleplansoftheform:S1(S–S1)whereS1isanynon-emptysubsetofS.RecursivelycomputecostsforjoiningsubsetsofStofindthecostofeachplan.Choosethecheapestofthe2n–2alternatives.Basecaseforrecursion:singlerelationaccessplanApplyallselectionsonRiusingbestchoiceofindicesonRiWhenplanforanysubsetiscomputed,storeitandreuseitwhenitisrequiredagain,insteadofrecomputingitDynamicprogramming JoinOrderOptimizationAlgorithmprocedurefindbestplan(S)if(bestplan[S].cost)returnbestplan[S]//elsebestplan[S]hasnotbeencomputedearlier,computeitnowif(Scontainsonly1relation)setbestplan[S].planandbestplan[S].costbasedonthebestwayofaccessingS/*UsingselectionsonSandindicesonS*/elseforeachnon-emptysubsetS1ofSsuchthatS1SP1=findbestplan(S1)P2=findbestplan(S-S1)A=bestalgorithmforjoiningresultsofP1andP2cost=P1.cost+P2.cost+costofAifcost10IfindexonAisusedtofindtuplessatisfyingA>10,andtuplesupdatedimmediately,sametuplemaybefound(andupdated)multipletimesSolution1:Alwaysdeferupdatescollecttheupdates(oldandnewvaluesoftuples)andupdaterelationandindicesinsecondpassDrawback:extraoverheadevenife.g.updateisonlyonR.B,notonattributesinselectionconditionSolution2:DeferonlyifrequiredPerformimmediateupdateifupdatedoesnotaffectattributesinwhereclause,anddeferredupdatesotherwise. JoinMinimizationJoinminimizationselectr.A,r.Bfromr,swherer.B=s.BCheckifjoinwithsisredundant,dropitE.g.joinconditionisonforeignkeyfromrtos,noselectiononsOthersufficientconditionspossibleselectr.A,s1.Bfromr,sass1,sass2wherer.B=s1.Bandr.B=s2.Bands1.A<20ands2.A<10joinwiths2isredundantandcanbedropped(alongwithselectionons2)Lotsofresearchinthisareasince70s/80s! MultiqueryOptimizationExampleQ1:select*from(rnaturaljoint)naturaljoinsQ2:select*from(rnaturaljoinu)naturaljoinsBothqueriessharecommonsubexpression(rnaturaljoins)Maybeusefultocompute(rnaturaljoins)onceanduseitinbothqueriesButthismaybemoreexpensiveinsomesituationse.g.(rnaturaljoins)maybeexpensive,plansasshowninqueriesmaybecheaperMultiqueryoptimization:findbestoverallplanforasetofqueries,expoitingsharingofcommonsubexpressionsbetweenquerieswhereitisuseful MultiqueryOptimization(Cont.)Simpleheuristicusedinsomedatabasesystems:optimizeeachqueryseparatelydetectandexploitingcommonsubexpressionsintheindividualoptimalqueryplansMaynotalwaysgivebestplan,butischeaptoimplementSharedscans:widelyusedspecialcaseofmultiqueryoptimizationSetofmaterializedviewsmaysharecommonsubexpressionsAsaresult,viewmaintenanceplansmaysharesubexpressionsMultiqueryoptimizationcanbeusefulinsuchsituations ParametricQueryOptimizationExampleselect*fromrnaturaljoinswherer.a<$1valueofparameter$1notknownatcompiletimeknownonlyatruntimedifferentplansmaybeoptimalfordifferentvaluesof$1Solution1:optimizeatruntime,eachtimequeryissubmittedcanbeexpensiveSolution2:ParametricQueryOptimization:optimizergeneratesasetofplans,optimalfordifferentvaluesof$1Setofoptimalplansusuallysmallfor1to3parametersKeyissue:howtodofindsetofoptimalplansefficientlybestonefromthissetischosenatruntimewhen$1isknownSolution3:QueryPlanCachingIfoptimizerdecidesthatsameplanislikelytobeoptimalforallparametervalues,itcachesplanandreusesit,elsereoptimizeeachtimeImplementedinmanydatabasesystems EndofChapter Figure13.01 Figure13.02 Figure13.03 Figure13.04 Figure13.06 Figure13.08'