数据结构课件PPT110章全 第二章.ppt 56页

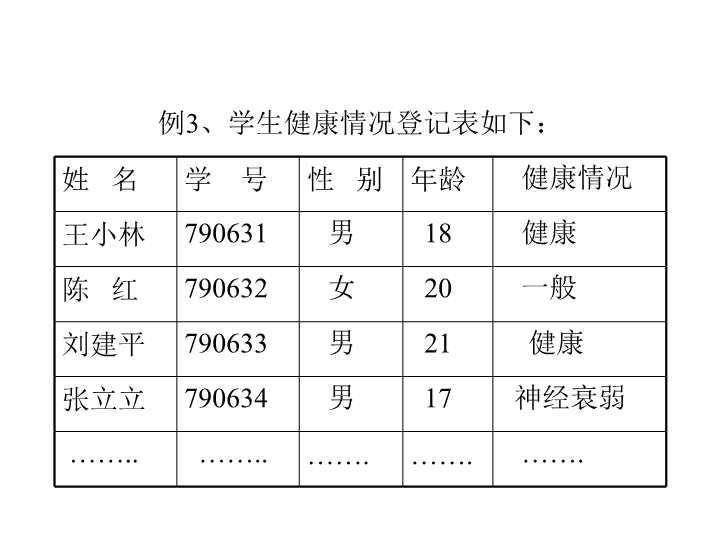
'第二章线性表2.1线性表的类型定义2.2线性表的顺序表示和实现2.3线性表的链式表示和实现2.3.1线性链表2.3.2循环链表2.3.3双向链表2.4一元多项式的表示及相加 2.1线性表的逻辑结构线性表(LinearList)：由n(n≧0)个数据元素(结点)a1，a2，…an组成的有限序列。其中数据元素的个数n定义为表的长度。当n=0时称为空表，常常将非空的线性表(n>0)记作：(a1，a2，…an)这里的数据元素ai(1≦i≦n)只是一个抽象的符号，其具体含义在不同的情况下可以不同。例1、26个英文字母组成的字母表（A，B，C、…、Z）例2、某校从1978年到1983年各种型号的计算机拥有量的变化情况。（6，17，28，50，92，188） 例3、学生健康情况登记表如下：姓名学号性别年龄健康情况王小林790631男18健康陈红790632女20一般刘建平790633男21健康张立立790634男17神经衰弱……..……..…….…….……. 例4、一副扑克的点数（2，3，4，…，J，Q，K，A）从以上例子可看出线性表的逻辑特征是：在非空的线性表，有且仅有一个开始结点a1，它没有直接前趋，而仅有一个直接后继a2；有且仅有一个终端结点an，它没有直接后继，而仅有一个直接前趋an-1；其余的内部结点ai(2≦i≦n-1)都有且仅有一个直接前趋ai-1和一个直接后继ai+1。线性表是一种典型的线性结构。数据的运算是定义在逻辑结构上的，而运算的具体实现则是在存储结构上进行的。抽象数据类型的定义为：P19 算法2.1例2-1利用两个线性表LA和LB分别表示两个集合A和B，现要求一个新的集合A=A∪B。1.[初值]获取线性表LA和LB2.[合并线性表]对于LB中的每一个元素做x如下操作：若（x不属于LA）则将x插入到LA的末尾3.[算法结束] 算法2.2例2-2巳知线性表LA和线性表LB中的数据元素按值非递减有序排列，现要求将LA和LB归并为一个新的线性表LC，且LC中的元素仍按值非递减有序排列。此问题的算法如下： 1.[初值]获取线性表LA和LB，并构造空线性表LC2.[选择插入元素]对于线性表LA和LB，都从其第一个元素开始做如下操作直到其中一个线性表元素全部遍历完毕：若（LA的元素a<=LB的元素b）则将元素a插入到LC的末尾，并选择LA中的下一个元素a否则将元素b插入到LC的末尾，并选择LB中的下一个元素b3.[补充剩下的元素]若（LA还有剩余元素）则将LA的剩余元素全部插入到LC末尾若（LB还有剩余元素）则将LB的剩余元素全部插入到LC末尾4.[算法结束] 2.2线性表的顺序存储结构2.2.1线性表把线性表的结点按逻辑顺序依次存放在一组地址连续的存储单元里。用这种方法存储的线性表简称顺序表。假设线性表的每个元素需占用l个存储单元，并以所占的第一个单元的存储地址作为数据元素的存储位置。则线性表中第I+1个数据元素的存储位置LOC(ai+1)和第i个数据元素的存储位置LOC(ai)之间满足下列关系：LOC(ai+1)=LOC(ai)+l线性表的第i个数据元素ai的存储位置为：LOC(ai)=LOC(a1)+(i-1)*l 由于C语言中的一维数组也是采用顺序存储表示，故可以用数组类型来描述顺序表。顺序表还应该用一个变量来表示线性表的长度属性，所以我们用结构类型来定义顺序表类型。这是一个动态分配的一维数组：#defineLIST_INIT_SIZE100#defineLISTINCREMENT10typedefstruct{ElemType*elem;intlength;intlistsize;}Sqlist; 初始化顺序存储的线性表StatusInitList_Sq(SqList&L){//构造一个空的线性表L.elem=(ElemType*)malloc(LIST_INIT_SIZE*sizeof(ElemType);if(!L.elem)exit(OVERFLOW);L.length=0;L.Listsize=LIST_INIT_SIZE;returnOK;} 2.2.2顺序表上实现的基本操作在顺序表存储结构中，很容易实现线性表的一些操作，如线性表的构造、第i个元素的访问。注意：C语言中的数组下标从“0”开始，因此，若L是Sqlist类型的顺序表，则表中第i个元素是l.data[i-1]。以下主要讨论线性表的插入和删除两种运算。1、插入线性表的插入运算是指在表的第i(1≦i≦n+1个位置上，插入一个新结点x， 使长度为n的线性表(a1，…ai-1，ai，…，an)变成长度为n+1的线性表(a1，…ai-1，x，ai，…，an) 1.[初值]获取线性表L，插入位置i，插入元素e2.[检查参数]若（插入位置超出线性表长度范围）则输出错误3.[检查空间]若（线性表空间不足）则分配新空间若（分配成功）则修改线性表的容量否则输出溢出错误4.[插入元素]将插入位置i以及其后的L中的元素全部后移一格将元素e插入位置i线性表长度增加15.[算法结束] 现在分析算法的复杂度。这里的问题规模是表的长度，设它的值为n。该算法的时间主要花费在循环的结点后移语句上，该语句的执行次数（即移动结点的次数）是n-i+1。由此可看出，所需移动结点的次数不仅依赖于表的长度，而且还与插入位置有关。当i=n+1时，由于循环变量的终值大于初值，结点后移语句将不进行；这是最好情况，其时间复杂度O（1）；当i=1时，结点后移语句将循环执行n次，需移动表中所有结点，这是最坏情况， 其时间复杂度为O（n）。由于插入可能在表中任何位置上进行，因此需分析算法的平均复杂度在长度为n的线性表中第i个位置上插入一个结点，令Eis(n)表示移动结点的期望值（即移动的平均次数），则在第i个位置上插入一个结点的移动次数为n-i+1。故不失一般性，假设在表中任何位置(1≦i≦n+1)上插入结点的机会是均等的，则p1=p2=p3=…=pn+1=1/(n+1)因此，在等概率插入的情况下， 也就是说，在顺序表上做插入运算，平均要移动表上一半结点。当表长n较大时，算法的效率相当低。虽然Eis(n)中n的系数较小，但就数量级而言，它仍然是线性阶的。因此算法的平均时间复杂度为O(n)。2、删除线性表的删除运算是指将表的第i(1≦i≦n)结点删除，使长度为n的线性表：(a1，…ai-1，ai，ai+1…，an)变成长度为n-1的线性表(a1，…ai-1，ai+1，…，an) 1.[初值]获取线性表L，删除位置i2.[检查参数]若（删除位置超出线性表长度范围）则输出错误3.[删除元素]获取删除位置i的元素e将删除位置i之后的L中的元素全部前移一格线性表长度减14.[算法结束] 该算法的时间分析与插入算法相似，结点的移动次数也是由表长n和位置i决定。若i=n，则由于循环变量的初值大于终值，前移语句将不执行，无需移动结点；若i=1，则前移语句将循环执行n-1次，需移动表中除开始结点外的所有结点。这两种情况下算法的时间复杂度分别为O(1)和O(n)。删除算法的平均性能分析与插入算法相似。在长度为n的线性表中删除一个结点，令Ede(n)表示所需移动结点的平均次数，删除表中第i个结点的移动次数为n-i，故式中，pi表示删除表中第i个结点的概率。在等 概率的假设下，p1=p2=p3=…=pn=1/n由此可得：即在顺序表上做删除运算，平均要移动表中约一半的结点，平均时间复杂度也是O(n)。2.3线性表的链式表示和实现线性表的顺序表示的特点是用物理位置上的邻接关系来表示结点间的逻辑关系，这一特点使我们可以随机存取表中的任一结点，但它也使得 插入和删除操作会移动大量的结点.为避免大量结点的移动，我们介绍线性表的另一种存储方式，链式存储结构，简称为链表(LinkedList)。2.3.1线性链表链表是指用一组任意的存储单元来依次存放线性表的结点，这组存储单元即可以是连续的，也可以是不连续的，甚至是零散分布在内存中的任意位置上的。因此，链表中结点的逻辑次序和物理次序不一定相同。为了能正确表示结点间的逻辑关系，在存储每个结点值的同时，还必须存储指示其后继结点的地址（或位置）信息，这个信息称为指针(pointer)或链(link)。这两部分组成了链表中的结点结构： 其中：data域是数据域，用来存放结点的值。next是指针域（亦称链域），用来存放结点的直接后继的地址（或位置）。链表正是通过每个结点的链域将线性表的n个结点按其逻辑次序链接在一起的。由于上述链表的每一个结只有一个链域，故将这种链表称为单链表（SingleLinked)。显然，单链表中每个结点的存储地址是存放在其前趋结点next域中，而开始结点无前趋，故应设头指针head指向开始结点。同时，由于终端结点无后继，故终端结点的指针域为空，即null（图示中也可用^表示)。例1、线性表:(bat，cat，eat，fat，hat，jat，lat，mat)datanext 单链表示意图如下：……………hat200…….……cat135eat170….……matNullbat130fat110…………jat205lat160…………165110130135160165170200205头指针 headbatcateatmat^…单链表是由表头唯一确定，因此单链表可以用头指针的名字来命名。例如：若头指针名是head，则把链表称为表head。用C语言描述的单链表如下：TypedefstructLnode{ElemTypedata;structLnode*next;}LNode,*LinkList; LNode*p;LinkListhead;注意区分指针变量和结点变量这两个不同的概念。指针变量P和（其值为结点地址）和结点变量*P之间的关系。P为动态变量，它是通过标准函数生成的，即p=(LNode*)malloc(sizeof(LNode));函数malloc分配了一个类型为LNode的结点变量的空间，并将其首地址放入指针变量p中。一旦p所指的结点变量不再需要了，又可通过标准函数free(p)释放所指的结点变量空间。 一、建立单链表假设线性表中结点的数据类型是字符，我们逐个输入这些字符型的结点，并以换行符‘n’为输入结束标记。动态地建立单链表的常用方法有如下两种：1、头插法建表该方法从一个空表开始，重复读入数据，生成新结点，将读入数据存放到新结点的数据域中，然后将新结点插入到当前链表的表头上，直到读入结束标志为止。 LinkListcreatelistf(void){charch;LinkListhead;LNode*p;head=null;ch=getchar();while(ch!=‵n′{p=(LNode*)malloc(sizeof(LNode));p–>data=ch;p–>next=head;head=p;ch=getchar();}return(head);} ListLinkcreatelist(intn){intdata;LinkListhead;LNode*p;head=null;for(i=n;i>0;--i){p=(LNode*)malloc(sizeof(LNode));scanf(“%d”，&p–>data);p–>next=head;head=p;}return(head);} 2、尾插法建表头插法建立链表虽然算法简单，但生成的链表中结点的次序和输入的顺序相反。若希望二者次序一致，可采用尾插法建表。该方法是将新结点插入到当前链表的表尾上，为此必须增加一个尾指针r，使其始终指向当前链表的尾结点。例： LinkListcreater(){charch;LinkListhead;LNode*p，*r;//(，*head;)head=NULL;r=NULL;while((ch=getchar()!=‵n′){p=(LNode*)malloc(sizeof(LNode));p–>data=ch;if(head==NULL)head=p;else{r–>next=p;r=p;}}if(r!=NULL)r–>next=NULL;return(head);} 说明：第一个生成的结点是开始结点，将开始结点插入到空表中，是在当前链表的第一个位置上插入，该位置上的插入操作和链表中其它位置上的插入操作处理是不一样的，原因是开始结点的位置是存放在头指针（指针变量）中， 而其余结点的位置是在其前趋结点的指针域中。算法中的第一个if语句就是用来对第一个位置上的插入操作做特殊处理。算法中的第二个if语句的作用是为了分别处理空表和非空表两种不同的情况，若读入的第一个字符就是结束标志符，则链表head是空表，尾指针r亦为空，结点*r不存在；否则链表head非空，最后一个尾结点*r是终端结点，应将其指针域置空。如果我们在链表的开始结点之前附加一个结点，并称它为头结点，那么会带来以下两个优点：a、由于开始结点的位置被存放在头结点的指针域中，所以在链表的第一个位置上的操作就 和在表的其它位置上的操作一致，无需进行特殊处理；b、无论链表是否为空，其头指针是指向头结点在的非空指针（空表中头结点的指针域为空），因此空表和非空表的处理也就统一了。其创建链表的算法如下： LinkListcreatelistr1(){charch;LinkListhead=(LinkList)malloc(sizeof(LNode));LNode*p，*r;r=head;while((ch=getchar())!=‵n′{p=(LNode*)malloc(sizeof(LNode));p–>data=ch;r–>next=p;r=p;}r–>next=NULL;return(head);} 上述算法里动态申请新结点空间时未加错误处理，可作下列处理：p=(LNode*)malloc(sizeof(LNode))if(p==NULL){error(〝Nospacefornodecanbeobtained〞);returnERROR;}以上算法的时间复杂度均为O(n)。 二、查找运算1、按序号查找在链表中，即使知道被访问结点的序号i，也不能象顺序表中那样直接按序号i访问结点，而只能从链表的头指针出发，顺链域next逐个结点往下搜索，直到搜索到第i个结点为止。因此，链表不是随机存取结构。设单链表的长度为n，要查找表中第i个结点，仅当1≦i≦n时，i的值是合法的。但有时需要找头结点的位置，故我们将头结点看做是第0个结点，其算法参考书本P29。 LNode*getnode(LinkListhead，inti){intj;LNode*p;p=head;j=0;while(p–>next&&jnext;j++;}if(i==j)returnp;elsereturnNULL;} 2、按值查找按值查找是在链表中，查找是否有结点值等于给定值key的结点，若有的话，则返回首次找到的其值为key的结点的存储位置；否则返回NULL。查找过程从开始结点出发，顺着链表逐个将结点的值和给定值key作比较。其算法如下： LNode*locatenode(LinkListhead，intkey){LNode*p=head–>next;while(p&&p–>data!=key)p=p–>next;returnp;}该算法的执行时间亦与输入实例中的的取值key有关，其平均时间复杂度的分析类似于按序号查找，也为O(n)。 三、插入运算插入运算是将值为x的新结点插入到表的第i个结点的位置上，即插入到ai-1与ai之间。因此，我们必须首先找到ai-1的存储位置，然后生成一个数据域为x的新结点p，并令结点ai-1的指针域指向新结点p，新结点p的指针域指向结点ai。从而实现三个结点ai-1，x和ai之间的逻辑关系的变化，插入过程如书本P29图2.8和算法2.9。 具体算法如下（以书本为准）voidinsertnode(linklisthead，datetypex，inti){listnode*p，*q;p=getnode(head，i-1);if(p==NULL)error(〝positionerror〞);q=(listnode*)malloc(sizeof(listnode));q–>data=x;q–>next=p–>next;p–>next=q;} 设链表的长度为n，合法的插入位置是1≦i≦n+1。注意当i=1时，getnode找到的是头结点，当i=n+1时，getnode找到的是结点an。因此，用i-1做实参调用getnode时可完成插入位置的合法性检查。算法的时间主要耗费在查找操作getnode上，故时间复杂度亦为O(n)。四、删除运算删除运算是将表的第i个结点删去。因为在单链表中结点ai的存储地址是在其直接前趋结点ai-1的指针域next中，所以我们必须首先找到 ai-1的存储位置p。然后令p–>next指向ai的直接后继结点，即把ai从链上摘下。最后释放结点ai的空间，将其归还给“存储池”。此过程见书P30算法2.10 具体算法如下：voiddeletelist(linklisthead，inti){listnode*p，*r;p=getnode(head，i-1);if(p==NULL||p–>next==NULL)returnERROR;r=p–>next;p–>next=r–>next;free(r);} 设单链表的长度为n，则删去第i个结点仅当1≦i≦n时是合法的。注意，当i=n+1时，虽然被删结点不存在，但其前趋结点却存在，它是终端结点。因此被删结点的直接前趋*p存在并不意味着被删结点就一定存在，仅当*p存在（即p!=NULL）且*p不是终端结点（即p–>next!=NULL）时，才能确定被删结点存在。显然此算法的时间复杂度也是O(n)。从上面的讨论可以看出，链表上实现插入和删除运算，无须移动结点，仅需修改指针。有序链表的合并见书本P31 有时候，也可以用一维数组来描述链表，这种链表称为静态链表。它的形式定义为Typedefstruct{ElemTypedata;//数据intcur;//指示下一项的数组索引}component,SLinkList[MAXSIZE];如图2.10，数组的第一个分量可以看成头结点，假设S为SLinkList型变量，则i=S[i].cur相当于指针的后移。定位函数见算法2.13，类似可以写出插入和删除的操作。所不同的是，用户必须自己实现malloc和free两个函数。例子见书P33 2.3.2循环链表循环链表是一种头尾相接的链表。其特点是无须增加存储量，仅对表的链接方式稍作改变，即可使得表处理更加方便灵活。单循环链表：在单链表中，将终端结点的指针域NULL改为指向表头结点或开始结点，就得到了单链形式的循环链表，并简单称为单循环链表。为了使空表和非空表的处理一致，循环链表中也可设置一个头结点。这样，空循环链表仅有一个自成循环的头结点表示。如下图所示： a1an….head⑴非空表⑵空表在用头指针表示的单链表中，找开始结点a1的时间是O(1)，然而要找到终端结点an，则需从头指针开始遍历整个链表，其时间是O(n) 在很多实际问题中，表的操作常常是在表的首尾位置上进行，此时头指针表示的单循环链表就显得不够方便.如果改用尾指针rear来表示单循环链表，则查找开始结点a1和终端结点an都很方便，它们的存储位置分别是(rear–>next)—>next和rear，显然，查找时间都是O(1)。因此，实际中多采用尾指针表示单循环链表。由于循环链表中没有NULL指针，故涉及遍历操作时，其终止条件就不再像非循环链表那样判断p或p—>next是否为空，而是判断它们是否等于某一指定指针，如头指什或尾指针等。 例、在链表上实现将两个线性表(a1，a2，a3，…an)和(b1，b2，b3，…bn)链接成一个线性表的运算。linklistconnect(linklistreara，linklistrearb){linklistp=reara—>next;reara—>next=(rearb—>next)—>nextfree(rearb—>next);rearb—>next=p;return(rearb);} 2.3.3双链表双向链表(Doublelinkedlist):在单链表的每个结点里再增加一个指向其直接前趋的指针域prior。这样就形成的链表中有两个方向不同的链，故称为双向链表。形式描述为：typedefstructDuLNode{ElemTypedata;structDuLNode*prior，*next;}DuLNode,*DuLinkList; 和单链表类似，双链表一般也是由头指针唯一确定的，增加头指针也能使双链表上的某些运算变得方便，将头结点和尾结点链接起来也能构成循环链表，并称之为双向链表。设指针p指向某一结点，则双向链表结构的对称性可用下式描述：(p—>prior)—>next=p=(p—>next)—>prior即结点*p的存储位置既存放在其前趋结点*(p—>prior)的直接后继指针域中，也存放在它的后继结点*(p—>next)的直接前趋指针域中。 双向链表的前插操作算法如下：StatusListInsert_DuL(DuLinkListp，ElemTypee){DuLinkLists=malloc(sizeof(DuLNode));s—>data=e;s—>prior=p—>prior;p—>prior—>next=s;s—>next=p;p—>prior=s;returnOK;} 删除p指针所指的结点，详见P37算法2.19{p–>prior–>next=p–>next;p–>next–>prior=p–>prior;free(p);}注意：与单链表的插入和删除操作不同的是，在双链表中插入和删除必须同时修改两个方向上的指针。上述两个算法的时间复杂度均为O(1)。 2.4一元多项式的表示及相加一元多项式一般情况下的一元多项式线性表表示抽象数据类型P40 表达式相加前的链表状态相加后的链表状态 1.[初值]获取线性表LA和LB2.[多项式相加]对于线性表LA和LB，都从其第一个元素开始做如下操作直到其中一个线性表元素全部遍历完毕：比较LA中的元素a与LB中的元素b的多项式指数（1）若（LA的元素a的指数LB的元素b的指数）则将元素b插入到LA的元素a之前，并选择LB的下一个元素b3.[补充剩下的元素]若（LB还有剩余元素）则将LB的剩余元素全部插入到LA末尾4.[算法结束]'