最新13.2.6--斜边直角边课件PPT.ppt 37页

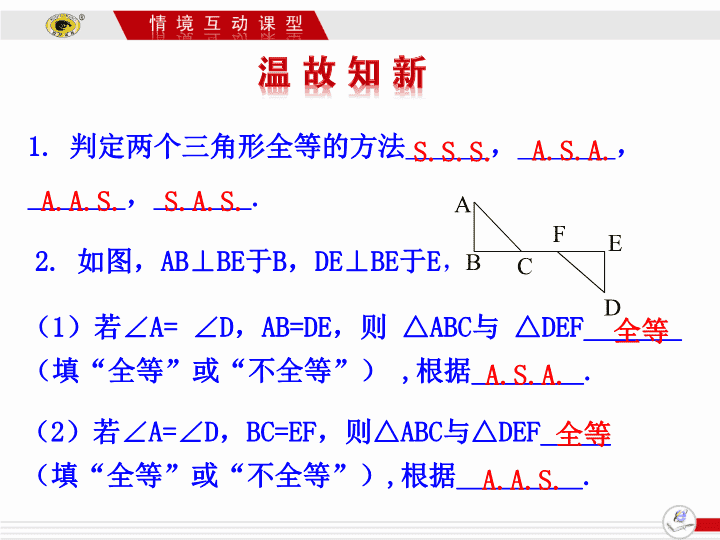
'13.2.6--斜边直角边 1.判定两个三角形全等的方法，，，.S.S.S.A.S.A.A.A.S.S.A.S.2.如图，AB⊥BE于B，DE⊥BE于E，（1）若∠A=∠D，AB=DE，则△ABC与△DEF_______（填“全等”或“不全等”）,根据________.ABCDEF全等A.S.A.（2）若∠A=∠D，BC=EF，则△ABC与△DEF_____（填“全等”或“不全等”）,根据_________.全等A.A.S. （3）若AB=DE，BC=EF，则△ABC与△DEF（填“全等”或“不全等”）,根据________.全等S.A.S.（4）若AB=DE，BC=EF，AC=DF,则△ABC与△DEF_______（填“全等”或“不全等”）,根据_______.S.S.S.全等 如果他只带了一个卷尺，能完成这个任务吗？工作人员测量了每个三角形没有被遮住的直角边和斜边，发现它们分别对应相等，于是他就肯定“两个直角三角形是全等的”.你相信他的结论吗？ 如图，已知两条线段（这两条线段长不相等），以长的线段为斜边、短的线段为一条直角边，画一个直角三角形.4cm5cm 按照下面的步骤做：1.画一线段AB，使它等于4cm.2.画∠MAB=90°.3.以点B为圆心，以5cm长为半径画弧，交射线AM于点C.4.连结BC.△ABC就是所求作的三角形.和其他同学所作的三角形进行比较，它们能重合吗？MABC 斜边和一条直角边分别相等的两个直角三角形全等.简记为H.L.（或斜边直角边）.ABCA′B′C′用符号语言表示为:在Rt△ABC和Rt△A′B′C′中,∵AB=A′B′,BC=B′C′,∴Rt△ABC≌Rt△A′B′C′.定理 你能够用几种方法说明两个直角三角形全等？直角三角形是特殊的三角形，所以不仅有一般三角形判定全等的方法:S.A.S.、A.S.A.、A.A.S.、S.S.S.，还有特殊的判定方法——“H.L.”. (1)_______,∠A=∠D(A.S.A.)(2)AC=DF,________(S.A.S.)(3)AB=DE,BC=EF()(4)AC=DF,______(H.L.)(5)∠A=∠D,BC=EF()(6)________,AC=DF(A.A.S.)BCAEFD把下列说明Rt△ABC≌Rt△DEF的条件或根据补充完整.AC=DFBC=EFH.L.AB=DEA.A.S.∠B=∠E 例1.如图,已知AC=BD,∠C=∠D=90°求证:BC=AD.ABDC证明:∵∠C=∠D=90°(已知），所以△ABC与△BAD都是直角三角形在Rt△ABC和Rt△BAD中，∵AC=BD(已知)，AB=BA(公共边)，∴Rt△ABC≌Rt△BAD（H.L.),∴BC=AD(全等三角形的对应边相等).【例题】 例2.如图，两根长度为12米的绳子，一端系在旗杆上，另一端分别固定在地面两个木桩上(两个木桩与旗杆底部在一条直线上)，两个木桩离旗杆底部的距离相等吗？请说明你的理由.分析：已知AB=AC=12，旗杆垂直于地面，则△ABD和△ACD是直角三角形. 解：BD=CD.∵∠ADB=∠ADC=90°，∴△ABD和△ACD都是直角三角形，在Rt△ABD和Rt△ACD中，AB=AC，AD=AD，∴Rt△ABD≌Rt△ACD(H.L.)，∴BD=CD. 例3.如图，有两个长度相同的滑梯，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系？ 解：∠ABC+∠DFE=90°.在Rt△ABC和Rt△DEF中,∵BC=EF,AC=DF，∴Rt△ABC≌Rt△DEF(H.L.).∴∠ABC=∠DEF(全等三角形的对应角相等).∵∠DEF+∠DFE=90°,∴∠ABC+∠DFE=90°. 1.如图，AC=AD，∠C，∠D是直角，将上述条件标注在图中，你能说明BC与BD相等吗？解：在Rt△ACB和Rt△ADB中,∵AB=AB,AC=AD,∴Rt△ACB≌Rt△ADB(H.L.),∴BC=BD(全等三角形的对应边相等).DCAB【跟踪训练】 2.已知：如图,AB⊥BD，CD⊥BD，AB=DC.求证：AD∥BC.证明：∵AB⊥BD，CD⊥BD∴∠ABD=∠CDB=90°在Rt△ABD和Rt△CDB中，∵AB=CD(已知),BD=DB(公共边)∴Rt△ABD≌Rt△CDB（H.L.)∴∠ADB=∠CBD∴AD∥BC. 3.已知：如图，在△ABC中，BD⊥AC，CE⊥AB，BD，CE交于O点，且BD=CE，求证：OB=OC.证明：∵BD⊥AC，CE⊥AB，∴∠BDC=∠CEB=90°.在Rt△BCD和Rt△CBE中，∵BD=CE，BC=CB，∴Rt△BCD≌Rt△CBE（H.L.)，∴∠CBD=∠BCE,∴OB=OC 通过本课时的学习，需要我们掌握2.会通过“斜边直角边”判定两个直角三角形全等.1.已知斜边和一直角边能作直角三角形.3.灵活运用条件，选择恰当的方法判定两个直角三角形全等. 3.如图，AB=AC,BE⊥AC于E，CF⊥AB于F,BE，CF相交于点D，则：(1)△ABE≌△ACF，(2)△BDF≌△CDE，(3)点D在∠BAC的平分线上.以上结论正确的有()A.只有（1）B.只有（2）C.只有（1）（2）D.（1）（2）（3） 【解析】选D.∵BE⊥AC,CF⊥AB,∴∠AEB=∠AFC=90°.又∵∠A=∠A,AB=AC,∴△ABE≌△ACF(A.A.S.),故（1）正确，∴AE=AF.又∵AB=AC,∴BF=CE,∴△BDF≌△CDE(A.A.S.),故（2）正确.连结AD,由于AE=AF,AD=AD,∴Rt△AFD≌Rt△AED(H.L.),∴∠FAD=∠EAD,故（3）正确，所以（1）（2）（3）均正确. 5.如图所示,有一个Rt△ABC，∠C=90°，AC=10cm,BC=5cm,一条线段PQ=AB，P，Q两点分别在AC上和过A点且垂直于AC的射线AM上运动，问P点运动到AC上的什么位置时，△ABC才能和△QPA全等？【解析】由题意可知：∠C=∠PAQ=90°，又AB=PQ，要使△ABC与△QPA全等，则只需AP=BC或AQ=BC即可，从而当点P运动至AC的中点即AP=5cm时，△ABC≌△QPA;或点P与点C重合即AP=AC=10cm时，△ABC≌△PQA. 6.如图，AB=AC，AD⊥BC于点D，AD=AE，AB平分∠DAE交DE于点F，请你写出图中三对全等三角形，并选取其中一对加以证明.【解析】(1)△ADB≌△ADC、△ABD≌△ABE、△AFD≌△AFE、△BFD≌△BFE、△ABE≌△ACD(写出其中的三对即可).（2）以△ADB≌△ADC为例证明.证明：∵AD⊥BC,∴∠ADB=∠ADC=90°,在Rt△ADB和Rt△ADC中,∵AB=AC,AD=AD,∴Rt△ADB≌Rt△ADC（H.L.）. 凡没有就着泪水吃过面包的人是不懂得人生之味的人——歌德 左右 请举起你的右手。说说右手可以做什么？请举起你的左手。说说左手可以做什么？ 我说你做。摸摸你的右耳。拍拍你的左腿。摸摸你的左耳。拍拍你的右腿。与你右边的同学握握手。 我说你摆。请你在桌上摆一支铅笔。请你在铅笔的左边摆一块橡皮。请你在铅笔的右边摆一本书。请你在数学书的左边摆一个本。请你在橡皮的左边摆一把尺子。 我问你答。铅笔的右边是（）。橡皮的左边是（）。本的左边有（）样物品。尺子的右边有（）样物品。 想一想老师举得是左手还是右手？为什么和小朋友举得相反呢？因为我们是面对面，方向相对，举得右手就刚好相反。动脑筋上下楼梯我们都是靠右边走，为什么不会撞上？ 跟着画一画，他象什么？在下边的里画一画1.在上面画一个2.在下面画一个3.在左面画一个4.在右面画一个5.在左面画一个大6.在左面画一个小'