最新2.2.3.向量共线定理解析课件PPT.ppt 50页

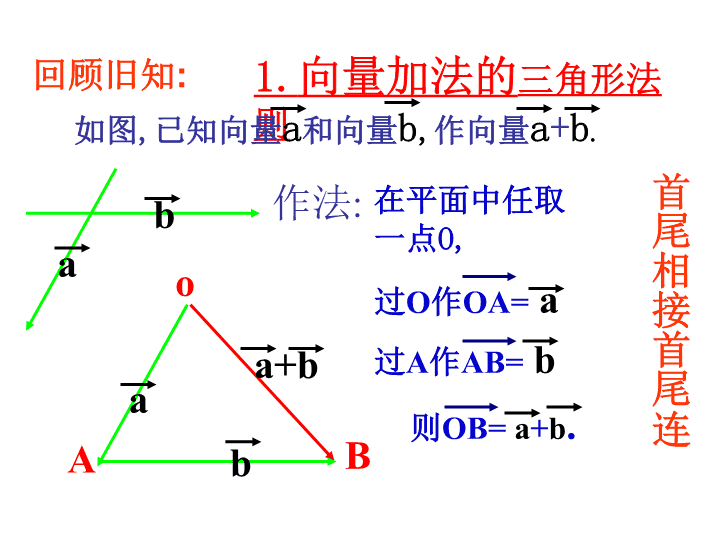
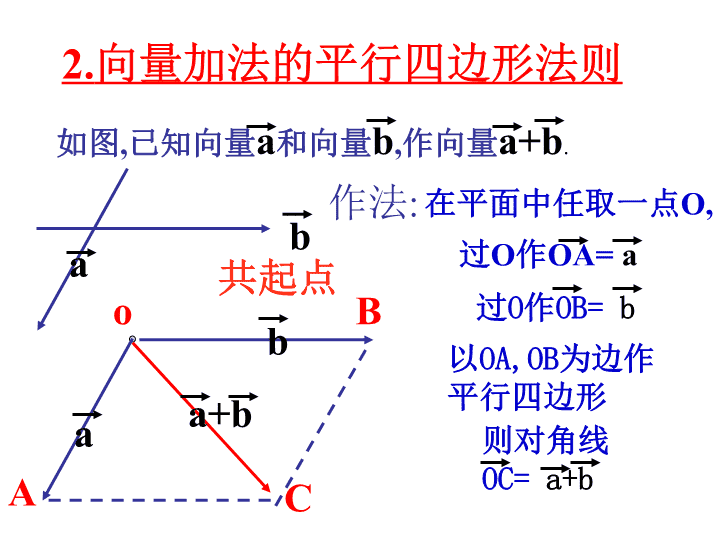
'2.2.3.向量共线定理解析 1.向量加法的三角形法则作法:在平面中任取一点O,o回顾旧知:过O作OA=a过A作AB=b则OB=a+b.a+bbaA如图,已知向量a和向量b,作向量a+b.bBa首尾相接首尾连 2.向量加法的平行四边形法则作法:在平面中任取一点O,o以OA,OB为边作平行四边形C如图,已知向量a和向量b,作向量a+b.baaAbB过O作OA=a过O作OB=ba+b则对角线OC=a+b共起点 OABC由图可知，向量OC=OA+AB+BC=a+a+a,我们把a+a+a记作3a，即OC=3a.显然，3a的方向与a的方向相同，3a的长度是a的长度的3倍，即|3a|=3|a|. PQMN由图可知，PN=PQ+QM+MN=(-a)+(-a)+(-a)，把(-a)+(-a)+(-a)记作-3a，即PN=-3a显然，-3a的方向与a的方向相反，-3a的长度是a的长度的3倍，即|-3a|=3|a|。 （1）一般地，我们规定实数λ与向量的积是一个向量，这种运算叫做向量的数乘，记作，它的长度和方向规定如下：（2）当时，的方向与的方向相同；当时，的方向与的方向相反。特别的，当时，思考:向量数乘和实数乘法有那些相同点?那些不同点?①a是一个向量；②a的长度等于的绝对值与向量a的长度的乘积。1、实数与向量积的定义 =2、实数与向量积的运算律根据定义，求作向量3(2a)和(6a)(a为非零向量)，并进行比较。 2、实数与向量积的运算律 2、实数与向量积的运算律ABCDEADE 2、实数与向量积的运算律结合律分配律分配律逆运算 设为实数，那么特别的，我们有向量的加、减、数乘运算统称为向量的线性运算.对于任意向量，以及任意实数，恒有 例1.计算：注：向量与实数之间可以像多项式一样进行运算. 练习Ｄ 解：DC=AB=aBC=BD+DC=(AD-AB)+DC=b-a+a=b-aMN=DN-DM=a-b-a=a-bDANMCB例1:梯形ABCD，且|AB|=2|DC|M、N分别为DC、AB中点。AB=aAD=b用a，b表示DC、BC、MN。 巩固练习:设D、E、F分别是ABC的边BC、CA、AB上的点,且AF=(1/2)AB,BD=(1/3)BC,CE=(1/4)CA.若记AB=m,CA=n.试用m,n表示DE、EF、FDABC·DE·F· 思考:问题2：如果向量a与b共线那么，b=λa？问题1：如果b=λa,那么，向量a与b是否共线？对于向量a(a≠0),b，以及实数λ, 3.向量共线定理反过来，已知向量a与b共线，a≠0，且向量b的长度是向量a的λ倍，即|b|︰|a|=λ，那么当向量a与b同向时，有b=λa，当向量a与b反向时，有b=-λa.也就是说：如果a与b共线，那么有且只有一个实数，使b=a.对于向量a（a≠0）、b，如果有一个实数，使b=a，那么由实数与向量的积的定义知，a与b共线. 思考：若　　　　则结论如何？ 练习、已知向量试判断，，是否共线。ABDEC ABDEC∴与共线．解： ABCO 例7:如图，在平行四边形ABCD中，M是AB的中点，点N是BD上的一点，，求证M、N、C三点共线.AMBCDN提示：设AB=aBC=b则MN=…=a+bMC=…=a+b所以M.N.C三点共线 一、①λa的定义及运算律②向量共线定理(a≠0)b=λa向量a与b共线二、定理的应用：1.证明向量共线2.证明三点共线:AB=λBCA,B,C三点共线3.证明两直线平行:AB=λCDAB∥CDAB与CD不在同一直线上直线AB∥直线CD 练习1设a，b是两个不共线向量。AB=2a+kbBC=a+bCD=a-2bA、B、D共线则k=_____(k∈R)解：BD=BC+CD=a+b+a-2b=2a-b2a+kb=λ(2a-b)=2λa-λb2=2λλ=-1k=-λk=-1∴k=-1∴ 练习2:e1、e2不共线,a=e1+e2,b=3e1-3e2.a与b是否共线。解：假设,a与b共线则e1+e2=λ(3e1-3e2)=3λe1-3λe21=3λ1=-3λ这样λ不存在。∴a与b不共线。 练习3:设两非零向量a和b不共线，如果AB＝a＋b，CD＝3（a－b），BC=2a+8b求证：A、B、D三点共线。 例2:（2003辽宁）已知四边形ABCD是菱形，P点在对角线AC上（不包括端点A、C），则AP等于()A、B、C、D、A 变形1:（2003全国）O是平面上一定点，A、B、C是平面上不共线的三个点，动点P满足则P的轨迹一定通过△ABC的()A．外心B．内心C．重心D．垂心B 变形2:OA、OB不共线，AP=tAB，用OA、OB表示OP所以：OABP因为OP=OA+AP=OA+tAB=OA+t(OB-OA)=(1-t)OA+tOB思考:若上式成立,则A、B、P有什么关系?反之? 结论：已知OA、OB不共线，若P、A、B三点共线则则P、A、B三点共线.若O是平面上任意一点,且若O是平面上任意一点,且其中,则P、A、B三点共线等价命题：OA、OB不共线，若P、A、B三点共线,则其中 巩固练习:如图OAB中,C为直线AB上一点,AC=λCB(λ≠-1),ABOC 练习1设a，b是两个不共线向量。AB=2a+kbBC=a+bCD=a-2bA、B、D共线则k=_____(k∈R)解：BD=BC+CD=a+b+a-2b=2a-b2a+kb=λ(2a-b)=2λa-λb2=2λλ=-1k=-λk=-1∴k=-1∴ 练习2:e1、e2不共线,a=e1+e2,b=3e1-3e2.a与b是否共线。解：假设,a与b共线则e1+e2=λ(3e1-3e2)=3λe1-3λe21=3λ1=-3λ这样λ不存在。∴a与b不共线。 练习3:设两非零向量a和b不共线，如果AB＝a＋b，CD＝3（a－b），BC=2a+8b求证：A、B、D三点共线。 Lesson23TheCornerStore课前自主预习课堂互动探究Unit4FoodandRestaurants 课前自主预习单词闯关1.钱["mʌnɪ]________2．冰箱[frɪdʒ]________3．二十["twentɪ]________4.传递；经过；路过[pɑːs]________5．角；角落["kɔːnə]________6．clerk[klɜːk]____________moneyfridgetwentyLesson23TheCornerStorepasscorner店员；办事员 短语互译1.取下；拿下________________2．分发；传送________________3．在冰箱里________________4.便利店________________5．manybottlesofcoke________________takedownpassaroundinthefridgecornerstores许多瓶可乐Lesson23TheCornerStore 句型在线1.这是一些钱。________________somemoney.2．你想要点什么？/需要帮忙吗？________I________you?3．我想要一杯茶。I"dlike________________________tea.HereisCanhelpacupofLesson23TheCornerStore 课堂互动探究词汇点睛passv.传递；经过；路过[观察]Takeonedown.Passitaround.拿下来一个。把它传递下去。Pleasepassthebooktome.请把这本书递给我。Passmethesalt,please.请把盐递给我。Lesson23TheCornerStore [探究]pass作动词，意为“传递；经过；路过”。当其作“传递”讲时，常构成短语passsb.sth.或passsth.tosb.，意为“把某物传递给某人”。Lesson23TheCornerStore 活学活用(1)根据汉语意思完成句子，每空一词请把这些面包递给你的弟弟。Please________thebread________yourbrother.(2)同义句转换Canyoupassmethenewspaper?Canyoupass__________________________________？passtothenewspapertomeLesson23TheCornerStore 句型透视1Hereissomemoney.这是一些钱。[探究]此句为倒装句，here引导倒装句的结构：(1)“Here＋be＋主语．”该句中主语为名词，be动词的数由后面主语的单复数形式决定。(2)“Here＋主语＋be.”其中主语为人称代词，be动词在数上与________保持一致。例如：Hereitis.它在这儿。主语Lesson23TheCornerStore 活学活用(1)这是四瓶牛奶。________________fourbottlesofmilk.(2)我们在这儿。Here________________．HereareweareLesson23TheCornerStore 2CanIhelpyou?你想要点儿什么？/需要帮忙吗？[探究]“CanIhelpyou？”是商店、饭店、旅馆、邮局、办事处等场所的服务人员对顾客的招呼语。类似的表达还有“WhatcanIdoforyou？/MayIhelpyou？”“IsthereanythingIcandoforyou？”。在不同的语境中可以表示不同的意思。在商店可译为“你想买/要点什么？”在饭店，可译为“你想吃点儿什么？”在售票处，可译为“你想要去哪里的票？”Lesson23TheCornerStore [拓展]常用的答语：(1)肯定回答：Yes,please.I"mlookingfor…/Iwanttobuy…/I"dliketobuy…(2)否定回答：No,thanks.I"mjustlookingaround./Ijusthavealook.Lesson23TheCornerStore 活学活用—CanIhelpyou?—________.IwanttobuysomeTshirtsformychildren.A.Yes,pleaseB.No,thanksC.Itdoesn"tmatterD.OfcourseIcanALesson23TheCornerStore'