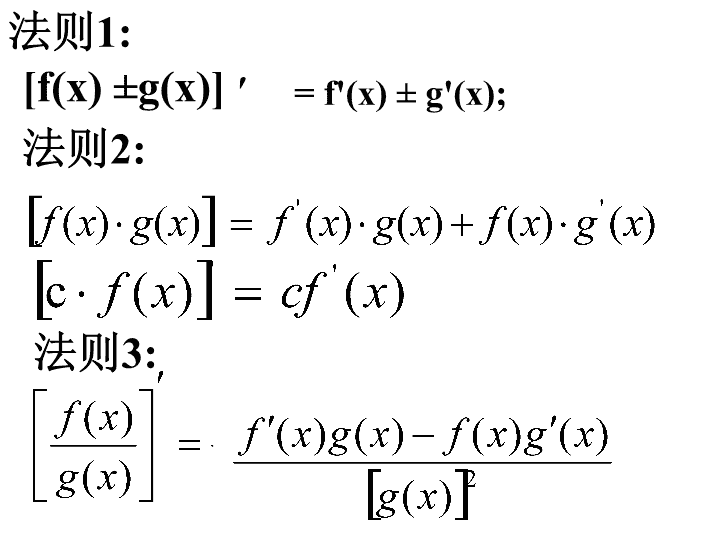最新北师大版：函数的单调性与导数公开课课件PPT.ppt 30页

'北师大版：函数的单调性与导数公开课 （4）.对数函数的导数:（5）.指数函数的导数:（3）.三角函数：（1）.常函数：(C)/0,(c为常数)；（2）.幂函数：(xn)/nxn1一、复习回顾：基本初等函数的导数公式 法则1:[f(x)±g(x)]′法则2:法则3:=f"(x)±g"(x); 一般地,设函数y=f(x)在某个区间（a,b）内可导,如果则f(x)为增函数；如果,则f(x)为减函数．如果在某个区间内恒有,一般地,设函数y=f(x)在某个区间（a,b）内可导,如果则f(x)为增函数；如果,则f(x)为减函数．则f(x)为常数函数.如果在某个区间内恒有函数单调性与导数正负的关系 例1已知导函数的下列信息:当14,或x<1时,当x=4,或x=1时,试画出函数的图象的大致形状.解:当14,或x<1时,可知在此区间内单调递减;当x=4,或x=1时,综上,函数图象的大致形状如右图所示.xyO14题型：应用导数信息确定函数大致图象 例2判断下列函数的单调性,并求出单调区间:解:(1)因为,所以因此,函数在上单调递增.题型：求函数的单调性、单调区间 例2判断下列函数的单调性,并求出单调区间:解:(2)因为,所以当,即时,函数单调递增;当,即时,函数单调递减.题型：求函数的单调性、单调区间 例2判断下列函数的单调性,并求出单调区间:解:(3)因为,所以因此,函数在上单调递减.(4)因为,所以当,即时,函数单调递增;当,即时,函数单调递减. 总结:当遇到三次或三次以上的,或图象很难画出的函数求单调性问题时，应考虑导数法。①求定义域②求③令④作出结论1°什么情况下，用“导数法”求函数单调性、单调区间较简便？2°试总结用“导数法”求单调区间的步骤？总结：注：单调区间不以“并集”出现。 练习判断下列函数的单调性,并求出单调区间: 例3如图,水以常速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中,请分别找出与各容器对应的水的高度h与时间t的函数关系图象.(A)(B)(C)(D)htOhtOhtOhtO 一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得快,这时,函数的图象就比较“陡峭”(向上或向下);反之,函数的图象就“平缓”一些.如图,函数在或内的图象“陡峭”,在或内的图象“平缓”.通过函数图像，不仅可以看出函数的增或减，还可以看出其变化的快慢，结合图像，从导数的角度解释变化快慢的情况。 一般地,设函数y=f(x)在某个区间（a,b）内可导,如果则f(x)为增函数；如果,则f(x)为减函数．如果在某个区间内恒有,一般地,设函数y=f(x)在某个区间（a,b）内可导,如果则f(x)为增函数；如果,则f(x)为减函数．则f(x)为常数函数.如果在某个区间内恒有函数单调性与导数正负的关系 总结:当遇到三次或三次以上的,或图象很难画出的函数求单调性问题时，应考虑导数法。①求定义域②求③令④作出结论1°什么情况下，用“导数法”求函数单调性、单调区间较简便？2°试总结用“导数法”求单调区间的步骤？总结：注：单调区间不以“并集”出现。 作业布置习题4-1A组第1,2题 例题（1）把一个正方形平均分成两个长方体，已知每个长方体的表面积是120平方厘米，求原正方体的表面积。 1.把一个正方体平均分成两个长方体，已知每个长方体的表面积是96平方厘米，求原正方体的表面积。2.把一个正方体木块平均锯成三个长方体，已知每个长方体的表面积是150平方厘米，求正方体的表面积。 3.一个正方体木块，把它平均分成两个长方体后，表面积增加了34平方厘米，求原正方体的表面积。 例题（2）一个棱长为16厘米的正方体（如图所示）。在一个侧面的中间处挖去一个长3厘米，宽3厘米，高16厘米的长方体后，剩下物体的表面积是多少平方厘米？ 1.一个长6厘米，宽4厘米，高8厘米的长方体木块，从一个侧面的中间处挖去一个棱长为2厘米的正方体的孔后，木块的表面积是多少？2.一个棱长是5厘米的正方体，从它的一个顶点处挖去一个棱长是1厘米的正方体后，剩下物体的表面积是多少？ 3.在一个长6厘米，宽4厘米，高3厘米的长方体积木上搭一个棱长为2厘米的正方体积木，所搭成物体的表面积是多少？ 例题（3）一个正方体，棱长是4分米。如果把它切成棱长是1分米的小正方体，这些小正方体的表面积之和是多少？ 1.把一个棱长是3分米的正方体切成棱长是1分米的小正方体，这些小正方体的表面积之和是多少？2.一个长方体长9厘米，宽6厘米，高5厘米，如果把它锯成棱长是1厘米的小正方体，一共可以锯多少个？这些小正方体的表面积之和是多少？ 3.用棱长是1厘米的小正方体搭成一个稍大一些的正方体，至少需要多少个小正方体？如果要搭一个棱长是7厘米的正方体，需要多少个小正方体？ 例题（4）一个正方体的表面涂满了红色，按右图所示切割，切开的小正方体中：（1）3个面涂色的有几个？（2）2个面涂色的有几个？（3）1个面涂色的有几个？（4）6个面都没有涂色的有几个？ 1.把一个体积为1立方分米的正方体木块的表面积涂上颜色，然后切成体积为1立方厘米的小正方体，在这些小正方体中，6个面都没有涂色的有多少个？2.把一个棱长是6厘米的正方体的6个面都涂满颜色，然后切成体积是1立方厘米的小正方体。在这些小正方体中，3个面都涂色的有几个？ 3.用若干个相同的小正方体搭成一个大的正方体，然后给大正方体的表面涂上颜色，已知2个面被涂上颜色的有36个，则这些小正方体一共有多少个？'