最新整理平面直角坐标系期末复习课件PPT幻灯片.ppt 41页

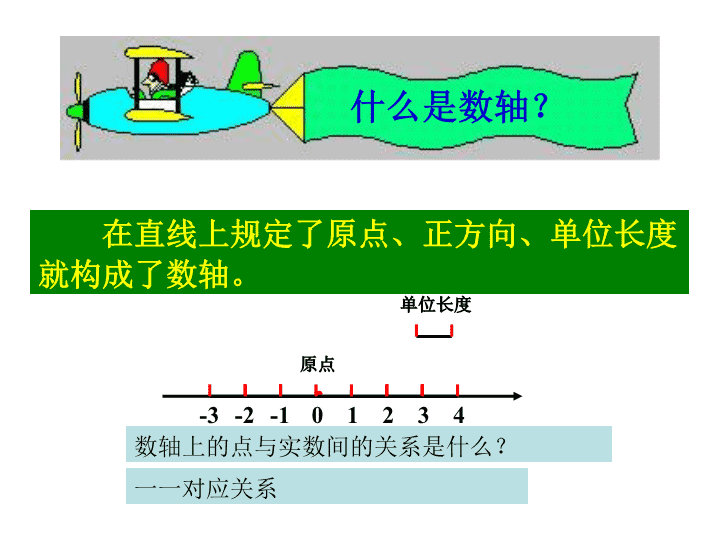
'整理平面直角坐标系期末复习课件PPT 复习目标1、正确建立平面直角坐标系，并会读点与描点2、掌握特殊位置点的坐标特点：（1）象限与象限内点的符号特点（2）坐标轴上的点的坐标特点（3）象限角平分线上的点的坐标特点3、掌握用坐标表示平移，关于X,Y轴对称等坐标系的应用 什么是数轴？在直线上规定了原点、正方向、单位长度就构成了数轴。·单位长度01234-3-2-1原点数轴上的点与实数间的关系是什么？一一对应关系 ·A31425-2-4-1-3012345-4-3-2-1x横轴y纵轴A的横坐标为4A的纵坐标为2有序数对(4,2)就叫做A的坐标横坐轴写在前面·B（-4,1）记作：（4,2） 对于坐标平面内的任意一点，都可以找到一个有序实数对（x,y)和它对应。这个有序实数对（x,y)就是这个点的坐标。 ·M（3，2）31425-2-4-1-3O12345-4-3-2-1x横轴y纵轴·N（2，3）S·R(1,-1)·(-1,1)pQA·(-3,-3)点P坐标(1,0)点Q坐标(0,-1)原点O坐标（0，0） 1.点Ｐ的坐标是（２，－３），则点Ｐ在第　　　象限．２．若点Ｐ（x，y）的坐标满足xy﹥０，则点Ｐ　　　　在第　　　　　　　　象限；若点Ｐ（x，y）的坐标满足xy﹤０，且在x轴上方，则点Ｐ在第　　　象限．３．若点Ａ的坐标是（－３，５），则它到x轴的距离是　　　　，到y轴的距离是　　　．４．若点Ｂ在x轴上方，y轴右侧，并且到x轴、y轴距离分别是２、４个单位长度，则点Ｂ的坐标是　　　　．５．点Ｐ到x轴、y轴的距离分别是２、１，则点Ｐ的坐标可能为　　　　　　　　　　　　　　　　　　　　．四一或三５３二（4，2）(1,2)、(1,-2)、(-1,2)、(-1,-2) １．想一想：下列各点分别在坐标平面的什么位置上？A（3，2）B（0，－2）C（－3，－2）D（－3，0）E（－1.5，3.5）F（2，－3）第一象限第三象限第二象限第四象限y轴上x轴上２．点P(x,y)的坐标x,y,满足xy=0,则点P在.4.甲同学从A(1,0)出发,向东走2个单位,再向北走3个单位到达B(,)5.点A(x,y)在第二象限,满足求A的坐标.6.点A(x,y),且x+y>0,那么点A在第___象限3.点A(1+m,2m+1)在x轴上,则m=___,此时A的坐标_______练一练 123456712345yO11524632345x例：找有序实数对（-2，3）在坐标平面上的对应点P。.P练习：在直角坐标系内画出下列各点：A（2，3），C（-2，-3），..AC点P（-2，3）关于X轴对称的点是点P（-2，3）关于Y轴对称的点是点A（2，3）关于原点对称的点是点C（-2，-3）点A（2，3）点C（-2，-3）点C（-2，-3） 01-11-1xy特殊点的坐标（x，０）（０，y）在平面直角坐标系内描出(-2,2),(0,2),(2,2),(4,2),依次连接各点,从中你发现了什么?平行于x轴的直线上的各点的纵坐标相同,横坐标不同.平行于y轴的直线上的各点的横坐标相同,纵坐标不同.在平面直角坐标系内描出(-2,3),(-2,2),(-2,0),(-2,-2),依次连接各点,从中你发现了什么? 012345-4-3-2-131425-2-4-1-3xyABCD 象限角平分线上的点的坐标特征已知p(x,y),填表：x=yx=-y (m,-m)(m,m)x＜0y＜0x＜0y＞0x＞0y＜0x＞0y＞0横坐标相同纵坐标相同(0,0)(0,y)(x,0)二四象限一三象限第四象限第三象限第二象限第一象限平行于y轴平行于x轴原点y轴x轴象限角平分线上的点点P（x，y）在各象限的坐标特点连线平行于坐标轴的点坐标轴上点P（x，y）特殊位置点的特殊坐标： 2.(1)点（-3，2）在第_____象限;二(2)点（1.5，-1）在第_______象限；四(3)点（-3，0）在____轴上；x(4)若点（-3，a+5）在x轴上，则a=______.-5(5)点M（-3，-4）到x轴的距离是_________，到y轴的距离是________,到原点的距离是________.435 解：ABCDxy03-32-2以长方形的中心为坐标原点，平行于BC、BA的直线为x轴、y轴，建立直角坐标系．坐标分别为A(-3，2)，B(-3，-2)，C(3，-2)，D(3，2) （七）两个图案对应点的坐标作如下变化，所得图案与原图案相比有什么变化？（1）对应点(x,y)变为(x+5,y)（2）对应点(x,y)变为(x-6,y)（3）对应点(x,y)变为(x,y+9)（4）对应点(x,y)变为(x,y-7)向右平移5个单位，形状不变，大小不变。向左平移6个单位，形状不变，大小不变。向上平移9个单位，形状不变，大小不变。向下平移7个单位，形状不变，大小不变。 3.将A(-3,2)向右平移4个单位,再向上平移1个单位得到B的坐标().五．点的平移.与点坐标的变化.1.将A(-3，2)向左平移2个单位,得点的坐标为.2.将A(-3，2)向下平移2个单位,得点的坐标为.5.将A(x，y)通过平移得点的坐标为A/(x+3，y-2)，则先A向平移个单位，再向平移个单位。4.将点A(2,3)向__平移__个单位,再向__平移__个单位后与点B(-3,5)重合6.A(1，2),B(2,3),将线段AB平移得到CD,点A的对应点C坐标为(0，4)，则点D的坐标为.（-5，2）（-3，0）1，3左5上2右3下2（1，5） 7、在直角坐标系中，点P（1，3）向下平移4个单位长度后的坐标为（）8、若点P（x，y）的坐标满足xy=0,则点P在（）A.（1，1）B.（1，-1）C.（1，0）D.（3，1）A.原点B.x轴上C.y轴上D.x轴上或y轴上或原点基础训练BD 3、已知点A（1+m，2m+1）在x轴上，则m=，此时坐标为。4、已知点A（5，2）和点B（-3，b），且AB∥x轴，则b=。1、点P（-2，-3）到x轴的距离为，到y轴的距离为。2、点P（3x-3，2-x）在第四象限，则x的取值范围是。巩固训练－0.5（0.5，0）232x＞2 已知点A（6，2），B（2，－4）。求△AOB的面积（O为坐标原点）典型例题例1CDxyO2424-2-4-2-4AB6 1.点P(3,0)在.2.点P(m+2,m-1)在y轴上,则点P的坐标是.3.点P(x,y)满足xy=0,则点P在.4.已知:A(1,2),B(x,y),AB∥x轴,且B到y轴距离为2,则点B的坐标是.5.点A(-1,-3)关于x轴对称点的坐标是.关于原点对称的点坐标是.6.若点A(m,-2),B(1,n)关于原点对称,则m=,n=.X轴正半轴上（0，-3）坐标轴上（-2，2）或（2,2）（-1，-3）（1，3）-12 ３２、海上救护中心收到一艘遇难船只的求救信号后发现该船位于点A（5，-4），同时发现在点B（5，2）和点C（-1，-4）处各有一艘救护船，如果救护船行使的速度相同，问救护中心应派哪条船前去救护可以在最短时间内靠近遇难船只？xyO-4-3-2-11234-12341-2-3A（5，-4）B（5，2）C（-1，-4） 3.点A在y轴上,距离原点4个单位.则A的坐标是.4.点A在y轴的右侧,距离y轴4个单位,距离x轴3个单位,则A的坐标是.三．平面上点的到坐标轴上的距离2.点P(a,b)到x轴的距离是,到y轴的距离是.1.点P(1,-4)到x轴的距离是,到y轴的距离是.6,点P(a-2,2a+3)到两坐标轴的距离相等,则a=.5.点P在x轴的下方,距离x轴4个单位;y轴的左侧,距离y轴的距离3个单位,则P的坐标是P()41 7.四边形Ａ(-2,1),B(3,-1),C(2,4),D(-1,2)将四边形ABCD向右平移２个单位，再向上平移１个单位，(1)求得到的另一个四边形各顶点的坐标(2).移动后的四边形的面积ABCD ABCDEF8.求四边形ABCD的面积 9.求三角形ABC的面积ABO 1.矩形ABCD的长为4,宽为3,建立适当的直角坐标系,并写出各点的坐标.31425-2-4-1-3012345-4-3-2-1ABCD31425-2-4-1-3012345-4-3-2-1还有其他方法吗xxyy六.建立适当的直角坐标系解题 从高考阅卷谈数学学习与高考复习 命题的思想、原则、目的：＊发挥数学的基础学科作用，考查中学数学知识＊主干内容重点考、数学概念深入考、数学问题简洁考、知识网络并联考、文理不同清晰考＊有利于中学数学教学，有利于高校人才选拔一、高考数学命题 ＊顺应课改，稳步推进一、高考数学命题新课程三年的试题特点与风格：＊情理之中，意料之外＊重视基础，文理不同 重点难点：重点：函数、数列、立体几何、圆锥曲线、空间线面（向量）、导数和概率。（新增内容中：零点及零点存在定理、函数模型应用、三视图、算法初步、茎叶图、合情推理等占一定比例）难点：函数、不等式、数列。 题型：选择题：10题×5分填空题：7题×4分解答题：5题，共72分（三角、数列，立体几何，解析几何，综合题）难度系数约在0.55－0.65 二、对考生的建议＊打好数学基础★＊提高运算能力★＊加强思维训练★＊培养创新意识★ 三、对数学学习和教学的建议＊注重基本概念理解，切忌照搬照套公式＊了解知识背景根源，知其然知其所以然＊切实掌握基本方法，着力训练基本运算＊深刻理解知识本质，不断创新解题方法＊归纳总结知识要点，纵览全局融会贯通 四、高考阅卷及答题注意事项♥浙江省每年考生数：约30万人♥阅卷老师数：约500人♥阅卷模式：电脑（网络）上阅卷；每题一个小组（选择题除外）阅卷情况：♥阅卷过程：预备会小组讨论标准大组确认阅卷阅卷：一评，二评三评四评抽查和统计 高考答题中应注意的问题（1）选择题：♥掌握好时间(不超过20分钟)；♥概念清楚，分析仔细。（2）填空题：♥看清题目要求；♥计算仔细，书写规范清楚。（3）解答题：♥写出关键步骤；♥将自己的分析计算尽量反映在答题纸上。（4）其他：♥不用铅笔答题；♥不作任何与答题无关的特殊记号。 浙江省高考近三年文理科试题分布情况相同题姊妹题不同题备注2007年10482008年10482009年84102010年35142011年4612 浙江省近三年高考（理科）数学重点内容分布内容2009年分数2010年分数2011年分数函数251829数列81314立体几何242425不等式151515圆锥曲线202424三角函数与平面向量222423概率与统计、排列、组合、二项式定理272213'