最新曹冲称象(第一课时)课件PPT.ppt 27页

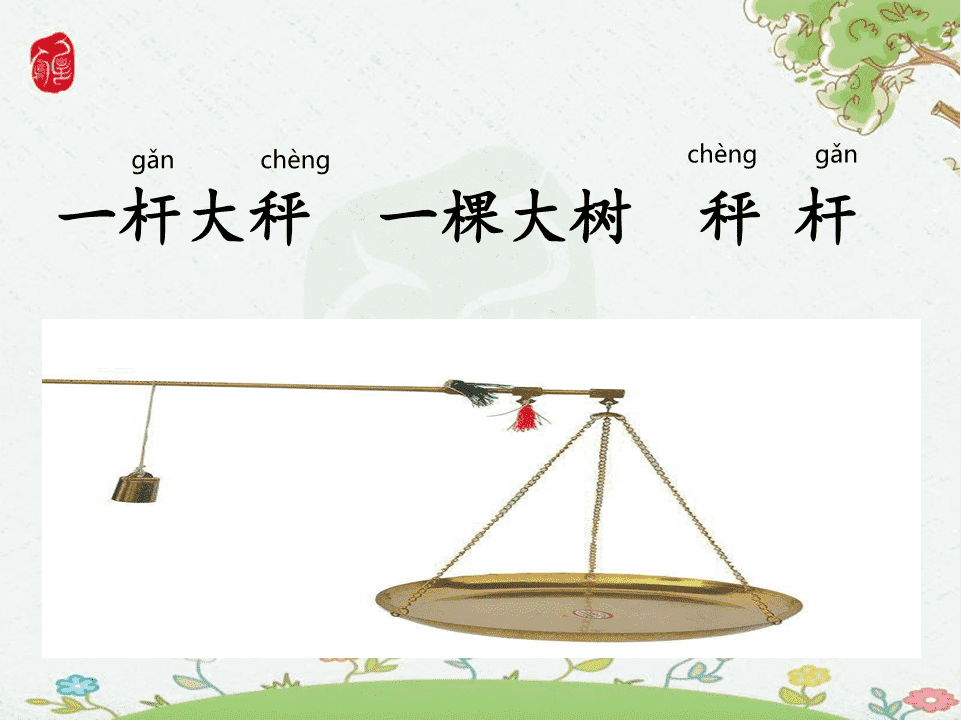
' 部教版二年级上册第一课时金陵中学实验小学金菊 gǎnchèngchènggǎn一杆大秤一棵大树秤杆chuán一头大象一堵墙一艘大船 曹操问：“谁有办法把这头大gǎn象称一称？”有的说：“得造一杆chèng大秤，砍一棵大树做秤杆。”有的说：“有了大秤也不行啊，谁有那么大的力气提得起这杆砍大秤呢？”曹操听了直摇头。 13曹操的儿子曹冲才七岁，他站24出来，说：“我有个办法。把大象赶到一艘大船上，看船身下沉多少，就沿着水面，在船舷上画一条线。再把大象赶上岸，往船上装石头，装到船下沉到画线的地方为止。停然止后称一称船上的石头。石头有多重，大象就有多重。” 曹操微笑着点一点头。他叫人照曹冲说的办法去做，果然称出了大象的重量。 称秤杆柱 称秤杆柱 变化率与导数 变化率问题导数研究的问题变化率问题研究某个变量相对于另一个变量变化的快慢程度． v问题1气球膨胀率我们都吹过气球回忆一下吹气球的过程,可以发现,随着气球内空气容量的增加,气球的半径增加越来越慢.从数学角度,如何描述这种现象呢?思考:这一现象v气球的体积V(单位:L)与半径r中，哪些量(单位:dm)之间的函数关系是4在改变？变3V(r)r量的变化情3v如果将半径r表示为体积V的函数,况？v那么3Vr(V)34 我们来分析一下:r(V)33V4v当V从0增加到1时,气球半径增加了r(1)r(0)0.62(dm)气球的平均膨胀率为r(1)r(0)0.62(dm/L)10v当V从1增加到2时,气球半径增加了r(2)r(1)0.16(dm)气球的平均膨胀率为r(2)r(1)0.16(dm/L)21显然随着气球体积逐渐0.62>0.16变大,它的平均膨胀率逐渐变小 思考?v当空气容量从V1增加到V2时,气球的平均膨胀率是多少?r(V)r(V)21VV21 问题2高台跳水在高台跳水运动中,运动员相对于水面的高度h(单位：米)与起跳后的时间t（单位：秒）存在函数关系hh(t)=-4.9t2+6.5t+10.如何用运动员在某些时间段内的平均速度粗略地描述其运动状态?ot 请计算0t0.5和1t2时的平均速度v:hh(t)=-4.9t2+6.5t+10oth(0.5)h(0)在0t0.5这段时间里，v4.05(m/s)0.50h(2)h(1)在1t2这段时间里，v8.2(m/s)21 探究:65计算运动员在0t这段时间里的平均速度,并49思考下面的问题:65hh()h(0)10v049t(1)运动员在这段时间里是静止的吗?(2)你认为用平均速度描述运动员的运动状态有什么问题吗?在高台跳水运动中,平均速度不能准确反映他在这段时间里运动状态. 平均变化率定义:f(x)f(x)l上述问题中的变化率可用式子21表示xx21称为函数f(x)从x1到x2的平均变化率v若设Δx=x2-x1,Δf=f(x2)-f(x1)这里Δx看作是对于x1的一个“增量”可用x1+Δx代替x2同样Δf=Δy=f(x2)-f(x1)ff(x)f(x)21则平均变化率为xxx21 理解：1，式子中△x、△f的值可正、可负，但△x值不能为0，△f的值可以为02，若函数f(x)为常函数时，△f=03,变式f(x)f(x)f(xx)f(x)2111xxx21 思考?v观察函数f(x)的图象yf(x)f(x)平均变化率21Y=f(x)xxx21yf(x2)B表示什么?f(x2)-f(x1)=△yAf(x1)x2-x1=△xx直线AB的Ox1x2斜率 练习v1、已知函数f(x)=-x2+x的图象上的一点A(-1,-2)及临近一点B(-1+Δx,-2+Δy),则Δy/Δx=(D)A、3B、3Δx-(Δx)2C、3-(Δx)2D、3-Δxv2、求y=x2在x=x0附近的平均速度。2x0+Δx 练习23.质点运动规律s=t+3,则在时间(3,3+t)中相应的平均速度为(A)9A.6+tB.6+t+tC.3+tD.9+tv4.物体按照s(t)=3t2+t+4的规律作直线运动,求在4s附近的平均变化率.253t 练习：v5.过曲线y=f(x)=x3上两点P（1，1）和Q(1+Δx,1+Δy)作曲线的割线，求出当Δx=0.1时割线的斜率. 小结：f(x)f(x)f(x)21v1.函数的平均变化率xxx21v2.求函数的平均变化率的步骤:(1)求函数的增量Δf=Δy=f(x2)-f(x1);ff(x)f(x)(2)计算平均变化率21xxx213.平均变化率是曲线陡峭程度的“数量化”，是一种粗略的刻画'