最新第3章Multisim元器件库及虚拟仪器1课件PPT.ppt 110页

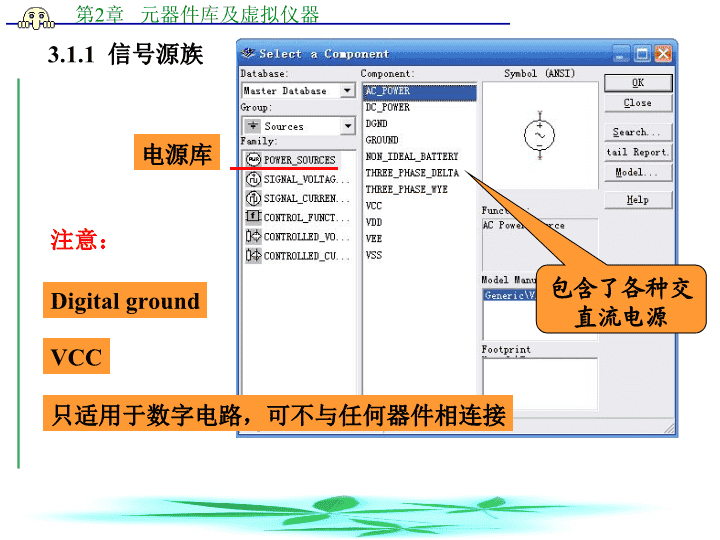
'第3章Multisim元器件库及虚拟仪器1 3.1元器件库介绍Multisim8为用户提供了如下元器件库：信号源（Sources）、基本元器件（Basic）、二极管（Diodes）、晶体管（Transistors）、模拟元器件（Analog）、TTL元器件(TTL)、CMOS元器件（CMOS）、其他数字元件（MiscellaneousDigital）、混合元件（Mixed）、指示元件（Indicators）、其他元件（Miscellaneous）、射频元件（RF）、机电类元件（Electro_Mechanical）。 3.1.1信号源族电源库包含了各种交直流电源注意：DigitalgroundVCC只适用于数字电路，可不与任何器件相连接 电流信号源库SIGNAL_CurrentSources Control_FunctionBlocks各种功能模块除法器、乘法器、积分器等 乘法器测试测试电路测试结果 积分器测试测试电路测试结果输入的三角波输出信号波形输入为矩形波输出信号波形 Controlled_VoltageSources各种压控源FSK_Voltage：频移键控信号源 测试电路测试结果频移键控信号源(FSKsource)测试 测试电路测试结果电压控制正弦波振荡器(Voltage-controlledsinewaveoscillator)测试 Controlled_CurrentSources各种受控电流源 3.1.2基本元件族 表3.2基本元器件库Relays 3.1.3二极管族 3.1.3二极管库（Diodes）表3.3二极管库(Diodes) 1.普通二极管（Diode）稳压二极管的主要参数是：稳定电压Uz、最小稳定电流Izmin、最大稳定电流Izmax、温度系数α。Uz>7V为正温度系数，Uz<5V为负温度系数。2.稳压二极管（ZenerDiode） 4.肖特基二极管（ShockleyDiode）该元件类似于标准二极管，具有单向导电性，但正向压降小，约0.1～0.3V，没有电容存储效应。3.LED发光二极管（LightEmittingDiode）注意：它的正向压降一般比普通二极管大，红色LED正向压降约1.1～1.2V，绿色LED的正向压降约1.4～1.5V。 5.全波桥式整流器（FullWaveBridgeRectifier）全波桥式整流电路 可控硅整流器简称SCR，又称固体闸流管。晶闸管是具有三个PN结的四层结构。引出的三个电极分别为阳极A，阴极K和控制极(或称门极)G。AGKPNPN阳极阴极控制极晶闸管的基本结构6.可控硅整流器（SiliconControlledRectifier） 工作原理S(c)S(a)S(b)可用下面的实验来说明晶闸管的工作原理。(1)晶闸管导通(灯亮)必须同时具备两个条件：第一，在阳极与阴极之间加正向电压；第二，控制极和阴极之间也要加正向电压(实际上加正触发脉冲)。(2)晶闸管导通后,断开控制极[图(b)所示]，晶闸管继续导通，即晶闸管一旦导通后，控制极就失去控制作用(这对普通晶闸管而言)。 (3)要使从导通转为阻断(截止)，必须切断阳极电源，或在阳极与阴极之间加反向电压，或将电流减小到某一数值(维持电流IH)以下。3.伏安特性导通阻断OIHIAUAUBRUBOIG0>IG1>IG2++从正向特性看，当UAP(ω1)，只能说是正常的可能性大。如要进行判断，只能通过化验来实现。4.1作为统计判别问题的模式分类 4.1.1贝叶斯判别原则例子设有一种诊断癌症的试验，其结果为“阳性”和“阴性”两种反应。若用这种试验来对一个病人进行诊断，提供的化验结果以模式x代表，这里x为一维特征，且只有x=“阳”和x=“阴”两种结果。4.1作为统计判别问题的模式分类 4.1.1贝叶斯判别原则例子假设根据临床记录，发现这种方法有以下统计结果患有癌症的人试验反应为阳性的概率=0.95，即p(x=阳|ω1)=0.95患有癌症的人试验反应为阴性的概率=0.05，即p(x=阴|ω1)=0.05正常人试验反应为阳性的概率=0.01，即p(x=阳|ω2)=0.01正常人试验反应为阴性的概率=0.99，即p(x=阴|ω2)=0.994.1作为统计判别问题的模式分类 4.1.1贝叶斯判别原则问题若被化验的人具有阳性反应，他患癌症的概率为多少，即求P(ω1|x=阳)=？这里P(ω1)是根据以往的统计资料得到的，为患癌症的先验概率。现在经过化验，要求出P(ω1|x=阳)，即经过化验后为阳性反应的人中患癌症的概率，称为后验概率。[计算]4.1作为统计判别问题的模式分类 4.1.2贝叶斯最小风险判别当考虑到对于某一类的错误判决要比对另一类的判决更为关键时，就需要把最小错误概率的贝叶斯判别做一些修正，提出条件平均风险rj(x)。M类分类问题的条件平均风险rj(x)对M类问题，如果观察样本被判定属于ωj类，则条件平均风险为：Lij称为将本应属于ωi类的模式判别成属于ωj类的是非代价。4.1作为统计判别问题的模式分类 4.1.2贝叶斯最小风险判别意义对于自然属性是属于ωi类的模式x来说，它来自ωi类的概率应为P(ωi|x)。如果分类器判别x是属于ωj类，但它实际上来自ωi类，也就是说分类器失败，这时Lij为失分，对应的条件风险为后验概率进行Lij的加权运算。由于模式x的自然属性可能来自M类中的任一类，因此可将观察样本指定为ωj类的条件平均风险用rj(x)的公式运算。4.1作为统计判别问题的模式分类 4.1.2贝叶斯最小风险判别Lij的取值若i=j，即判别正确，得分，Lij可以取负值或零，表示不失分。若i<>j，即判别错误，失分，Lij应取正值。最小平均条件风险分类器分类器对每一个模式x有M种可能的类别可供选择。若对每一个x计算出全部类别的平均风险值r1(x),r2(x),…,rM(x)，并且将x指定为是具有最小风险值的那一类，则这种分类器称为最小平均条件风险分类器。表达式4.1作为统计判别问题的模式分类 4.1.2贝叶斯最小风险判别两类（M=2）的情况[例子]一般多类（M类）的情况4.1作为统计判别问题的模式分类 出发点当已知或者有理由设想类概率密度函数P(x|ωi)是多变量的正态分布时，上一节介绍的贝叶斯分类器可以导出一些简单的判别函数。由于正态密度函数易于分析，且对许多重要的实际应用又是一种合适的模型，因此受到很大的重视。4.2正态分布模式的贝叶斯分类器 M种模式类别的多变量正态类密度函数判别函数是一个超二次曲面。对于正态分布模式的贝叶斯分类器，两个模式类别之间用一个二次判别界面分开，就可以求得最优的分类效果。两类问题且其类模式都是正态分布的特殊情况当C1<>C2时的情况显然，判别界面d1(x)-d2(x)=0是x的二次型方程，即ω1和ω2两类模式可用二次判别界面分开。当x是二维模式时，判别界面为二次曲线，如椭圆，圆，抛物线或双曲线等。当C1=C2=C时的情况判别界面为x的线性函数，为一超平面。当x是二维时，判别界面为一直线。4.2正态分布模式的贝叶斯分类器 [例子]讨论贝叶斯分类规则是基于统计概念的。如果只有少数模式样本，一般较难获得最优的结果。4.2正态分布模式的贝叶斯分类器 作业及编程设以下模式类别具有正态概率密度函数：ω1：{(00)T,(20)T,(22)T,(02)T}ω2：{(44)T,(64)T,(66)T,(46)T}（1）设P(ω1)=P(ω2)=1/2，求这两类模式之间的贝叶斯判别界面的方程式。（2）绘出判别界面。编写两类正态分布模式的贝叶斯分类程序。（可选例题或上述作业题为分类模式） 在贝叶斯分类器中，构造分类器需要知道类概率密度函数p(x|ωi)。如果按先验知识已知其分布，则只需知道分布的参数即可。例如：类概率密度是正态分布，它完全由其均值向量和协方差矩阵所确定。对均值向量和协方差矩阵的估计即为贝叶斯分类器中的一种参数估计问题。4.3均值向量和协方差矩阵的参数估计 参数估计的两种方式一种是将参数作为非随机变量来处理，例如矩估计就是一种非随机参数的估计。另一种是随机参数的估计，即把这些参数看成是随机变量，例如贝叶斯参数估计。4.3均值向量和协方差矩阵的参数估计 均值和协方差矩阵的非随机参数的估计均值和协方差矩阵的估计量定义均值和协方差矩阵估计量的迭代运算4.3均值向量和协方差矩阵的参数估计 均值向量和协方差矩阵的贝叶斯学习将概率密度函数的参数估计量看成是随机变量θ，它可以是纯量、向量或矩阵。按这些估计量统计特性的先验知识，可以先粗略地预选出它们的密度函数。通过训练模式样本集{xi}，利用贝叶斯公式设计一个迭代运算过程求出参数的后验概率密度p(θ|xi)。当后验概率密度函数中的随机变量θ的确定性提高时，可获得较准确的估计量。4.3均值向量和协方差矩阵的参数估计 均值向量和协方差矩阵的贝叶斯学习一般概念单变量正态密度函数的均值学习4.3均值向量和协方差矩阵的参数估计'