最新10非零和博弈报告课件PPT.ppt 37页

'进入夏天，少不了一个热字当头，电扇空调陆续登场，每逢此时，总会想起那一把蒲扇。蒲扇，是记忆中的农村，夏季经常用的一件物品。　　记忆中的故乡，每逢进入夏天，集市上最常见的便是蒲扇、凉席，不论男女老少，个个手持一把，忽闪忽闪个不停，嘴里叨叨着“怎么这么热”，于是三五成群，聚在大树下，或站着，或随即坐在石头上，手持那把扇子，边唠嗑边乘凉。孩子们却在周围跑跑跳跳，热得满头大汗，不时听到“强子，别跑了，快来我给你扇扇”。孩子们才不听这一套，跑个没完，直到累气喘吁吁，这才一跑一踮地围过了，这时母亲总是，好似生气的样子，边扇边训，“你看热的，跑什么？”此时这把蒲扇，是那么凉快，那么的温馨幸福，有母亲的味道！　　蒲扇是中国传统工艺品，在我国已有三千年多年的历史。取材于棕榈树，制作简单，方便携带，且蒲扇的表面光滑，因而，古人常会在上面作画。古有棕扇、葵扇、蒲扇、蕉扇诸名，实即今日的蒲扇，江浙称之为芭蕉扇。六七十年代，人们最常用的就是这种，似圆非圆，轻巧又便宜的蒲扇。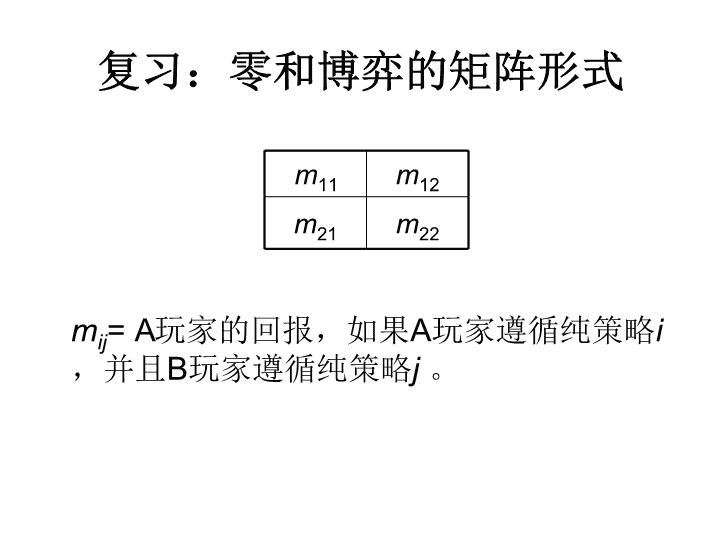　　蒲扇流传至今，我的记忆中，它跨越了半个世纪，也走过了我们的半个人生的轨迹，携带着特有的念想，一年年，一天天，流向长长的时间隧道，袅10非零和博弈报告 概要非零和博弈的矩阵形式及其基本概念严格控制及其应用博弈平衡的定义关键结果：任何有限博弈都存在平衡合作与非合作之间的区别连续性博弈及相应方法 复习：零和博弈的矩阵形式m11m12m21m22mij=A玩家的回报，如果A玩家遵循纯策略i，并且B玩家遵循纯策略j。 示例的作用虽然简单，但此例子可模拟很多不同的实际情况，在这些场合中参与者获得类似的奖励。合作：俩人做同一个项目。每个人可选择努力工作或休息。如果A勤奋工作后就宁肯去休息了，但俩人工作要比俩人休息有一个好的结局。双巨头：两家公司竞争生产同一产品，并且都想使利润最大化。他们能制定两种价格，高价与低价。如果两公司都选择高价，则他们都实现利润1000块。如果他们都选低价，则他们都实现薄利600块。否则，高价公司盈利1200块，而低价公司损失200块。军备竞赛、机器人探测、公共财产使用、…… 非零和博弈的矩阵形式供罪不供罪供罪-5,-50,-10不供罪-10,0-1,-1BA这不是零和博弈。玩家的收益（回报）不再是相反的了。假设俩玩家都是理性的，每位玩家遵循的最佳策略是什么？ 控制性策略供罪不供罪供罪-5,-50,-10不供罪-10,0-1,-1BA不管B选怎样的策略，A供罪的回报比不供罪的大。A不需要考虑不供罪，因为这不可能带来更高的回报。 控制性策略供罪不供罪供罪-5,-50,-10不供罪-10,0-1,-1BA对B也是同样道理：不管A选怎样的策略，B供罪的回报比不供罪的大。B不需要考虑不供罪，因为这不可能带来更高的回报。 控制性策略供罪不供罪供罪-5,-50,-10不供罪-10,0-1,-1BA一个策略是严格控制性(占优)的，是指在应对对手每步可能的行动上，该策略比任何其它策略产生的回报都高。关键结果：如果俩玩家都有严格控制性的策略，则他们为对弈提供了一个解，即预测对弈的结局。一种控制性策略的平衡。供罪是A的一个严格控制性策略供罪是B的一个严格控制性策略因此，（供罪，供罪）是解。 IIIIIIIVI3,04,15,95,6II5,35,89,79,0III3,38,46,36,3IV2,83,12,34,5迭代消去受控策略更一般性结论：能安全地消去任何严格受控策略。即，绝不会选这样的策略为博弈的一个解，因为在应对对手的每步可能的行动上，该策略比任何其它现存策略产生的回报都低。迭代消去受控策略是简化与求解博弈过程的第一步。此方法充分吗？ IBIIBIIIBIA-1,66,-15,4IIA6,-1-1,65,4IIIA4,54,57,7控制性策略怎样玩此博弈？在此场合，不能保证俩人，甚至一人有一个控制性策略。仍能用迭代消去法来简化博弈：消去严格受控策略，因为决不能选它们作为解。然而，需要更一般方法来寻找博弈的解，即预测有理性的人怎样博弈。需要一个定义来推广零和博弈的定义。 IBIIBIIIBIA-1,66,-15,4IIA6,-1-1,65,4IIIA4,54,57,7怎样玩此博弈？对于A的任何策略X，uA(IIIA,IIIB)uA(X,IIIB)对于B的任何策略Y，uB(IIIA,IIIB)uB(IIIA,Y)（IIIA,IIIB）是一种平衡，因为：在B采用IIIB策略下，A不能找到一个比IIIA更好的策略了。同样，在A采用IIIA策略时，B也不能找到比IIIB一个更好的策略。 俩玩家以上能直接将俩人的形式扩展到更多人。如有n个玩家，则需要定义n个回报函数ui，i=1,…,n。回报函数ui把一个n元组策略转换为玩家i的相应回报。ui(s1,…,sn)=玩家i的回报，如果玩家1,…,n采用纯策略s1,…,sn。其它的定义(如控制性策略等)则保持不变。 形式化定义一个n元组纯策略(s*1,…,s*n)是一个纯平衡，如对任何玩家i及其采用的任何策略si，有：即，玩家i不能找到一个比s*i更好的策略了，如果其他玩家使用该平衡中的其余策略。称为一个纯Nash平衡（NE）。 等同的形式化定义一个n元组纯策略(s*1,…,s*n)是一个纯平衡，如对所有的i，有：即，玩家i不能找到一个比s*i更好的策略了，如果其他玩家使用该平衡中的其余策略。称为一个纯Nash平衡（NE）。 问题已把求解博弈的概念推广到非零和博弈，即NE。基本问题：总存在一个NE吗？它唯一吗？ 多NE的例子左右左+1,+1-1,-1右-1,-1+1,+1两辆车正相向而行，它们有两种选择：靠右开或靠左开。为什么多NE是一个问题？因为NE的回报可能各不相同。 多NE的例子乒乓球电影乒乓球+2,+10,0电影0,0+1,+2俩朋友有不同的嗜好，A喜欢看乒乓球比赛，但B却喜欢看电影。俩人都不愿意一个人去看。换句话说，每人都宁愿去看对方喜欢的，也不愿单独去看自己喜欢的。 无纯NE的例子IIII0,+1+1,0II+1,00,+1甚至很简单的博弈也可能没有一个纯策略平衡。这并不奇怪，因为零和博弈也有类似的问题，即不一定有一个纯策略解。解决方法：与零和博弈一样的思路，即允许玩家随机采用混合策略。 混合策略平衡能将平衡概念扩展到混合策略。在此场合，每位玩家i的一个混合策略是一个概率矢量pi=(pij)，其中，pij为i玩家选择j纯策略的概率。一组混合策略(p*1,…,p*n)的平衡：如果把p*i改变为任何其它混合策略pi，则i玩家都将得到一个较低的回报。 例子乒乓球电影乒乓球+2,+10,0电影0,0+1,+2一个混合策略是：A选择乒乓球的概率为p=2/3B选择乒乓球的概率为q=1/3实际上，这是该对弈的混合策略平衡。对A与B，期望回报都是2/3。 例子乒乓球电影乒乓球+2,+10,0电影0,0+1,+2A选择乒乓球的概率为p，B选择乒乓球的概率为q。A的期望回报是：uA=(+2)pq+(+1)(1-p)(1-q)=1-p-q+3pqB的期望回报是：uB=(+1)pq+(+2)(1-p)(1-q)=2-2p-2q+3pq在平衡时，因为uA(p*,q*)极大，所有uA对p的导数是零。因此，3q*-1=0，q*=1/3。同样在平衡时，uB对q的导数是零。因此，3p*-2=0，p*=2/3。 关键结果定理：对有限玩家的任何博弈，至少存在一个平衡。可能不存在纯策略平衡，但至少存在一个混合策略平衡。任何平衡都是在迭代消去受控策略后余下的。 计算平衡：示例A与B两家公司生产同一产品。单件产品成本是c，因此生产qA件产品的成本是C=cqA。市场价格依总产量来定：P=(qA+qB)。如果(qA+qB)>，则置P=0。因此，A公司的收入是qA(c(qA+qB))。问题：怎样算出A与B公司的最佳产量？如果他们产量过高，则价格就会下降，因此每家公司的收入也会下降。如果他们产量过少，收入也会少。 示例对A公司而言，qA的每个可能值都是一个纯策略。对B公司也有相似的结论。平衡时，随qA而变的A的收入达到极大。因此，在NE时，qA(c(qA+qB))对qA的导数是零。同样地，平衡时，随qB而变的B的收入达到极大。因此，在NE时，qB(c(qA+qB))对qB的导数是零。因此，(q*A,q*B)是下面方程组的解：c2qAqB=0，c2qBqA=0。解为：q*A=q*B=(c)/3。每家公司的收入为(c)2/9 NE就是俩玩家的最佳表现吗？假设不是独立地去寻找一个A与B的平衡，而是去使总收入极大：即计算总收入对总产量qA+qB的导数为零，则在qA=qB=(c)/4时，收入达到极大。这相当于每家公司收入(c)2/8，它大于由NE算得的收入。因此，公司可以运作得比理论预测的更好，对吗？ 协调与非协调理论没什么错。原因是，在第二种计算中，俩公司是合作的，而不是相互独立地选择其策略。一般情况是，任何博弈中，如果玩家同意合作、协调、交流，则他们可获得一个更高的回报。例如，在囚犯两难中，明显的答案是囚犯都拒绝供罪，前提是他们事先同意协调他们的行动。仅考虑无协调的博弈，可产生似非而是的结果。 公共绿地的悲剧下例表明，上例只是一个更一般情形下的个案：n个农夫用一片公共绿地放羊。因为这片绿地是由所有农夫共享的一个有限资源，所以羊越多，吃的也越少，使得它们的价值下降。如果农夫们都合作，则通过总利润最大化，每位农夫获得一个较高的盈利；如果他们利用NE，理性行动，则盈利较低。在后一种场合，每位农夫都试图耗尽这片公共资源。注意：换一个例子只需将公共绿地换成，比如说能源、通讯带宽、石油，…，把农夫换成客户、机器人、汽车、公司、…。 NE方法NE存在于迭代消去受控策略后余下的策略中。迭代消去是到达NE的一种方法。对于上例所示的由连续变量描述的策略，可通过求解下面ui对si的导数等于零这样的方程组来寻找NE：并保留值最大的解。 总结非零和博弈的矩阵形式及其基本概念严格控制及其应用博弈平衡的定义关键结果：任何有限博弈都存在（可能是混合性的）平衡理解合作与非合作之间的区别连续性博弈及相关方法 学习数学你最棒啦!一、速算与巧算4.5÷3.6=（4.5÷9）÷（3.6÷9）=0.5÷0.4=1.25 12.02÷0.25=（12.02x4）÷(0.25x4)=48.08÷1=48.08 第一关：小试牛刀：4.82÷0.8+3.18÷0.8（3.6+7.2）÷0.36772.2÷7.818.18÷1.8=（4.82+3.18）÷0.8=10+20=10=3.6÷0.36+7.2÷0.36=30=8÷0.8=（780-7.8）÷7.8=780÷7.8-7.8÷7.8=100-1=99=（18+0.18）÷1.8=18÷1.8+0.18÷1.8=10+0.1=10.1 第二关：平稳度过：28÷3.516÷0.253.6÷2.4 第三关：过关斩将15.26÷3.5+9.24÷3.5150.15÷1.57.6÷1.4+6.3÷1.4+2.9÷1.46.3÷8+0.125x3.732.8÷5+7.2÷5'