最新人力资源年终述职报告课件PPT.ppt 38页

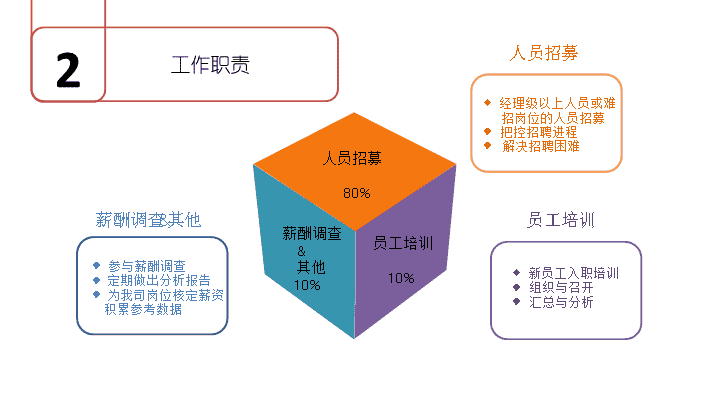
'人力资源年终述职报告 目录个人介绍2014年度工作总结2015年度工作规划问题与建议人才推荐3年内个人职业规划 人员招募80%员工培训10%薪酬调查&其他10%薪酬调查&其他◆参与薪酬调查◆定期做出分析报告◆为我司岗位核定薪资积累参考数据员工培训人员招募工作职责2◆经理级以上人员或难招岗位的人员招募◆把控招聘进程◆解决招聘困难◆新员工入职培训◆组织与召开◆汇总与分析 8其他各部门招聘需求汇总其他：38人（单位：人） 9广州分公司招聘需求汇总 10招聘完成情况及相关数据汇总到场率:21%合格率：47%入职率：80%（单位：人） 112013年度与2014年度各招聘数据比较110%75%120%130%158%76%95%（单位：人） 12入职人员统计及目前在册情况实际入职人数:187人目前在职人数：95人新入员工保有率：所反映出的问题：说明企业员工正处于动荡之中，管理本身存在较大的问题。所带来的影响：员工情绪波动，企业凝聚力下降。同时，因离职而产生的替代性招聘增多，直接造成了人员资本及组织效能的增加。解决之道：“留人”是关键。50% 入职失败分析无公积金提及10次提及33次试用期长提及40次提及13次薪资过低补助缺失行业差距提及4次入职失败48人13 同行业公司薪酬结构状况比较(以项目经理为例)项目经理平均薪资：8.6K/月其他福利：住房公积金交通补助通讯补助入股分红项目提成我司项目经理平均薪资：6.6K/月14 招聘渠道使用效果分析80人58人20人17人6人3人3人网络招聘（智联招聘&前程无忧&猎聘网&58同城）●以上合作网站均为全国性综合人才网，以覆盖面广、简历数量多、针对性强等优势，一直以来作为我司最主要的招聘渠道。●依据本年度入职人员简历来源分析可见，智联招聘高居榜首，占比44%，适合普通员工及中层人员的招募。但由于地域性差异，智联招聘更适合北方地区，可作为我司总部人员的招募。前程无忧则更适合南方地区，可作为我司广州分公司及驻地人员招募之用。●通过猎聘网入司3人，数量虽少，但均为经理、总监级人员，人才质量明显高于其他人才网站，因为此网站适合高端人才招募。●通过58同城入职3人，由于网站不够专业，简历数量有限，人才质量及岗位匹配度差，已取消2015年度的合作。内部推荐&同行推荐●通过以上两种方式入职78人，与智联招聘几乎持平。通过此途径入职的员工多为内部员工熟知的朋友或同事，他们对公司内部信息和岗位要求有准确认识。此外，此类新员工也能更快地融入公司关系网络，得到更多有效的职业指导，因而，离职率低、适应度强、工作满意度较好。因此可作为我司招募新员工，尤其是项目执行类岗位人员招募的有效途径。●但此种方式需要有成熟的内部推荐奖励机制来支持。猎头公司推荐●本年度与我司合作比较密切的猎头公司有2家，分别是恭圣和铭阳。在入职的6人中，其中4人由恭圣推荐，2人由铭阳推荐。在招商、客户开拓、设计、创意策划等岗位方面均有覆盖。对于高端型管理型人才的招募，猎头公司来源更为有效。15 猎头公司合作明细16目前正在与猎头合作的职位：创意总监公关总监BD总监未来涉及到猎头互换职位的人数：2人原美术指导-曾松原市场部总监-陈雅兰有关具体的替补人选产生的费用要具体根据新入职人员薪资而定。 招聘流程运用情况开始提出招聘需求职位审核部门总监签批总经理签批确认岗位要求发布招聘信息初试复试终试作出录用决策作出录用决策确认职位信息与候选人谈薪发出OFFER薪资确认单的签批薪资确认单的签批人力资源部中心用人部门结束17 招聘成果187人招聘组2人234人80%4提报完成完成比18 招聘成果比较及经验分享人员缩减完成比+44%80%36%201420131.人才吸引●“三天一发布”法●“多名称包装”法●规范岗位JD2.人才甄选●提升简历筛选效率●提高准确度3.面试与录用●加强沟通、灌输招聘管理理念。●推动用人部门主动参与招聘全过程。4.调整与修正●随时调整招聘方向及策略（如：人力配置、用人标准、薪资等）19 问题与建议无人用无人知无人留●建立企业文化用企业魅力吸引人●优化公司官方网站加强对外企宣力度●加强人才内部培养（如：促销项目经理）●加强部门梯队建设对于重点岗位应有意识地培养“继任者”●健全薪资福利体提供良好的晋升通道●注重各管理层领导力提升●加强团队建设加强企业与员工的粘合度20 21员工培训流程调整内容扩充重组与规划课件制作做了什么？重新对员工培训做了整体规划并重组结构，使培训更为规范与系统。对培训内容做了全面的修改，主题更加明确突出、流程更加顺畅。重新制作所有培训课件及相关支持文件。加入突出“爱与感恩”主题的观看视频环节及员工分享交流环节。特别是分享环节的员工参与度高达100%，反映良好。这为创造良好的工作氛围、打造融洽的同事关系设立了基础。 22新员工入职培训实施情况：112人：82人：30人培训内容：公司简介、人事、行政、IT管理制度培训人次：应到112人实到82人，请假30人答卷人次：112人（请假人员均已于培训之后补写试卷。） 计划实施评估无全年培训计划培训内容与方式单一培训经费投入不足加大培训力度针对公司不同层面的员工开展具有针对性的多项培训。对于稀缺岗位应开展职业技能专项培养计划。．重视度欠缺激励与约束机制不健全管理层应首先加大对培训的重视程度，并给予相关支持。培训应与晋升、绩效相挂钩，提高员工对培训的重视程度。缺乏训前评估培训的跟踪与反馈不够培训开展前应先做培训需求问卷，了解员工的真实需求点。训后评估做到位，评价实际效果。23 不足loss25WeChat招聘平台没有开展起来首次英文培训试讲失败与个别业务部门沟通不够顺畅EnglishClass slogan26满足岗位需求保证人才储备实现梯队建设 如何达成目标27123严把招聘流程控制好时间节点使面试流程紧凑有效加大企业宣传力度拓展新的招聘途径尝试校园招聘提高薪资及各项福利以顺应市场行情提高工作效率45Days 在此输入标题输入文字在此录入上述图表的综合分析结论在此录入上述图表的综合分析结论在此录入上述图表的综合分析结论在此录入上述图表的综合分析结论““谢谢您的聆听！ 在此输入标题输入文字在此录入上述图表的综合分析结论在此录入上述图表的综合分析结论在此录入上述图表的综合分析结论在此录入上述图表的综合分析结论““有问必答…… 无穷递缩等比数列的应用授课人：李振华（2005-05）长沙市周南中学 问题提出：我们先来看一篇阅读材料——一位古希腊学者芝诺（Zenon，公元前496～前429）曾提出一个著名的“追龟”诡辩题。大家知道，乌龟素以动作迟缓著称，阿基里斯则是古希腊传说中的英雄和擅长跑步的神仙。芝诺断言：阿基里斯与龟赛跑，将永远追不上乌龟！其理由是：如图所示，假定阿基里斯现在A处，乌龟现在T处。为了赶上乌龟，阿基里斯先跑到乌龟的出发点T，当他到达T点时，乌龟已前进到T1点；当他到达T1点时，乌龟又已前进到T2点，如此等等。当阿基里斯到达乌龟前次到达过的地方，乌龟已又向前爬动了一段距离。因此，阿基里斯是永远追不上乌龟的！ATTT1T1T2 让我们再看一看乌龟所走过的路程:设阿基里斯的速度是乌龟的十倍，龟在前面100米。当阿基里斯跑了100米时，龟已前进了10米；当阿基里斯再追10米时，龟又前进了1米，阿再追1米，龟又进了0.1米所以阿基里斯追上乌龟所必须跑过的路程为右端显然为一无穷递缩等比数列的和，根据以前学过的公式及极限定义有所以，阿基里斯只要坚持不到112米的路程就可以追上乌龟！S= 牛刀小试之熟练公式篇：如何把0.化成分数形式？0.=0.3+0.03+0.003+==分析： 实战演练篇：解：正方形的面积组成一个无穷递缩等比数列，首项为a1=a2，由于相邻的两个正方形中小正方形与大正方形的边长比为,所以面积比即公比q=，因此所有正方形的面积之和为S=BaDCA1—（1）例1、在边长为a的正方形ABCD内依次作内接正方形AiBiCiDi（ｉ=1，2，3）如图1—（1）使内接正方形的四个顶点恰为相邻前一个正方形边的中点，求所有正方形的面积之和； 变式：如果使内接正方形与相邻前一正方形的一边的夹角为，如图1—（2）求所有正方形的面积之和。DCBAA1B1C1D11—（2）分析：正方形的面积仍然组成一个无穷递缩等比数列，首项为a1=a2,先求相邻的两个正方形中小正方形与大正方形的边长比——如图令A1D1=x,则a所以边长比为面积比即公比q为从而所有正方形的面积和为 经验积累：与实际问题结合的无穷递缩等比数列的求和问题，关键是求出首项及公比，求公比时，要特别注意相邻两个图形之间的联系。解：设第n次被剪去的半圆面积为an（n=1，2，3）,则a1=a2=a3=它们组成一个无穷递缩等比数列,故所有这些被剪掉部分的面积和为则例2.如图所示，Ｐ是一块半径为１的半圆形纸板，在Ｐ的左下端剪去一个半径为的半圆后得图形P1，然后依次剪去更小半圆（其半径为前一被剪掉半圆的半径一半）得图形记被剪剩下的纸板Pn的面积为Sn，求Sn。 探索创新篇如图，封闭图形P表示抛物线弧y=x2（）与x轴及直线x=2围成的图形,如何求封闭图形的面积?P AiBi分析：把区间[0,2]n等分,分别过分点Ai(ｉ=1，2，3•••n-1)作x轴的垂线,交抛物线于Bi,如图作n-1个矩形。我们可以先求：(1)求这n-1个矩形的面积和;再求(2)求 小结：1、理解无穷递缩等比数列（公比|q|<1)，尽管项数无限，但它的和是一个确定的数.2、与实际问题结合的无穷递缩等比数列的求和问题，关键是求出首项及公比，求公比时，要特别注意相邻两个图形之间的联系。谢谢大家，请各位老师指正！ 一艘太空飞船飞往地球，第一次观测时发现一个正三角形（边长为1个单位）的军事建筑物如图（1），第二次观测时如图（2）发现它每边中央1/3处还有一个正三角形，第三次观测时如图（3）还发现原先每一小边的中央1/3处又有一向外突出的正三角形…把第1、2、3…n次观测到的军事建筑物的面积分别记为a1、a2、a3…an，求an的表达式；如果我们把an的极限记作建筑物的实际面积，求这个面积。课外思考题：'