最新函数的对称性与函数的图象变换总结课件PPT.ppt 70页

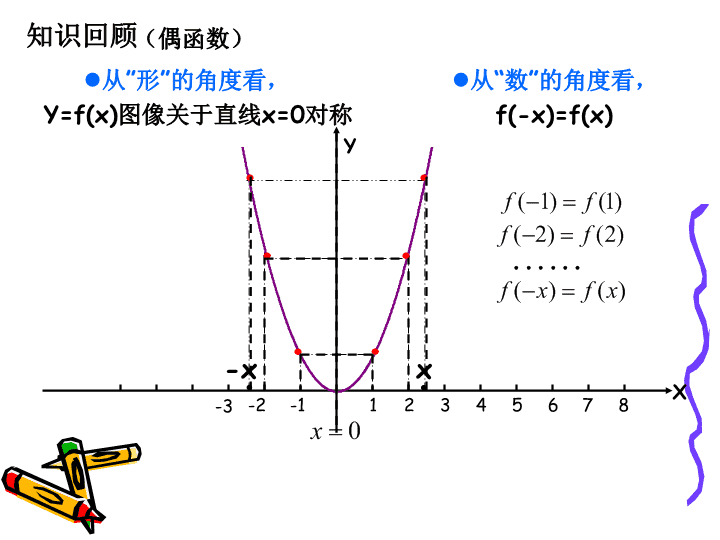
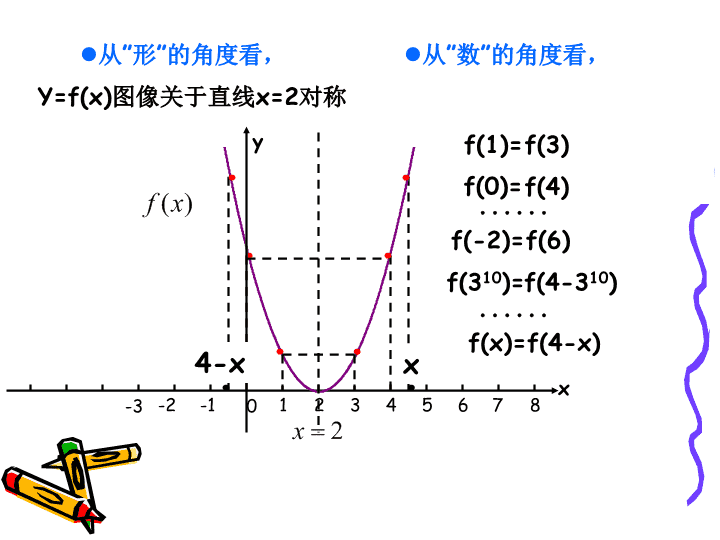
'函数的对称性与函数的图象变换总结 1-3-1-2165432-xx78（偶函数）Y=f(x)图像关于直线x=0对称知识回顾从”形”的角度看，从“数”的角度看，f(-x)=f(x)XY 1-3-1-216543278f(x)=f(4-x)f(1)=f(0)=f(-2)=f(310)=f(6)f(4-310)0x4-xY=f(x)图像关于直线x=2对称f(3)f(4)从”形”的角度看，从”数”的角度看，xy f(x)=-f(2a-x)f(a-x)=-f(a+x)xyoa从”形”的角度看，从”数”的角度看，中心对称性类比探究a+xa-xy=f(x)图像关于(a,0)中心对称b af(a+x)=2b-f(a-x)f(2a-x)=2b-f(x)b中心对称性y=f(x)图像关于(a,b)中心对称类比探究xyo 思考？(1)若y=f(x)满足f(a-x)=-f(b+x),(2)若y=f(x)满足f(a-x)=2c-f(b+x),则函数图像关于对称a+b2(,0)点则函数图像关于对称a+b2(,C)点 -xx函数图像关于直线x=0对称f(-x)=f(x)函数图像关于直线x=a对称f(a-x)=f(a+x)x=af(x)=f(2a-x)函数图像关于(0,0)中心对称函数图像关于(a,0)中心对称f(-x)=-f(x)f(a-x)=-f(a+x)f(x)=-f(2a-x)轴对称中心对称性a 练习:(1)若y=f(x)满足f(-2-x)=f(-2+x),则函数图像关于对称(2)若y=f(x)满足f(3-x)=f(4+x)(4)若y=f(x)满足f(3-x)=-f(4+x)(3)若y=f(x)满足f(-2-x)=-f(-2+x),(5)若y=f(x)满足f(3-x)=3-f(4+x) 函数图象的变换及应用函数图象是研究函数的重要工具,它能为所研究函数的数量关系及其图象特征提供一种”形”的直观体现,是利用”数形结合”解题的重要基础. 描绘函数图象的两种基本方法:①描点法;(通过列表﹑描点﹑连线三个步骤完成)②图象变换;(即一个图象经过变换得到另一个与之相关的函数图象的方法)函数图象的三大变换平移对称伸缩 问题1：如何由f(x)=x2的图象得到下列各函数的图象？（1）f(x-1)=(x-1)2（2）f(x+1)=(x+1)2（3）f(x)+1=x2+1（4）f(x)-1=x2-1Oyxy=f(x-1)y=f(x+1)y=f(x)-1y=f(x)+1函数图象的平移变换：左右平移y=f(x)y=f(x+a)a>0,向左平移a个单位a<0,向右平移|a|个单位上下平移y=f(x)y=f(x)+kk<0,向下平移|k|个单位k>0,向上平移k个单位11-1-1 同步练习:①若函数f(x)恒过定点(1,1),则函数f(x-4)-2恒过定点.②若函数f(x)关于直线x=1对称,则函数f(x-4)-2关于直线对称.(5,-1)x=5 问题2.设f(x)=(x>0)，求函数y=-f(x)、y=f(-x)、y=-f(-x)的解析式及其定义域，并分别作出它们的图象。xxyo1y=f(x)xxyo1y=f(x)xxyo1y=f(x)y=-f(x)y=f(-x)y=-f(-x)对称变换（1）y=f(x)与y=f(-x)的图象关于对称；（2）y=f(x)与y=-f(x)的图象关于对称；（3）y=f(x)与y=-f(-x)的图象关于对称；x轴y轴原点 练习：说出下列函数的图象与指数函数y=2x的图象的关系，并画出它们的示意图.(1)y=2-x(2)y=-2x(3)y=-2-xOyOyOy11-11-1xxx 1.函数y=f(-x)与函数y=f(x)的图像关于y轴对称2.函数y=-f(x)与函数y=f(x)的图像关于x轴对称3.函数y=-f(-x)与函数y=f(x)的图像关于原点对称4.函数y=f(x)与函数y=f(2a-x)的图像关于直线对称函数图象对称变换的规律:思考:“函数y=f(x)与函数y=f(2a-x)的图像关于直线x=a对称”与“函数y=f(x)满足f(x)=f(2a-x),则函数y=f(x)关于直线x=a对称”两者间有何区别?对称变换是指两个函数图象之间的对称关系,而”满足f(x)=f(2a-x)或f(a+x)=f(a-x)有y=f(x)关于直线x=a对称”是指一个函数自身的性质属性,两者不可混为一谈.x=a 问题3：分别在同一坐标系中作出下列各组函数的图象，并说明它们之间有什么关系？（1）y=2x与y=2|x|Oxy由y=f(x)的图象作y=f(|x|)的图象：y=2x保留y=f(x)中y轴右侧部分，再加上y轴右侧部分关于y轴对称的图形.1y=2|x| Oyx-414-1由y=f(x)的图象作y=|f(x)|的图象：保留y=f(x)在x轴上方部分，再加上x轴下方部分关于x轴对称到上方的图形 函数图象的对称变换规律：（1）y=f(x)y=f(x+a)a>0,向左平移a个单位a<0,向右平移|a|个单位上下平移（2）y=f(x)y=f(x)+kk>0,向上平移k个单位k<0,向下平移|k|个单位（1）y=f(x)与y=-f(x)的图象关于对称；（2）y=f(x)与y=f(-x)的图象关于对称；（3）y=f(x)与y=-f(-x)的图象关于对称；函数图象的平移变换规律：(4)由y=f(x)的图象作y=f(|x|)的图象：保留y=f(x)中部分，再加上这部分关于对称的图形.(6)由y=f(x)的图象作y=|f(x)|的图象：保留y=f(x)中部分，再加上x轴下方部分关于对称的图形.x轴y轴原点y轴右侧y轴x轴上方x轴左右平移 练习：已知函数y=f(x)的图象如图所，分别画出下列函数的图象：yox1-1-212-0.5(1)y=f(-x);(2)y=-f(x).yox1-1-212-0.5y=f(-x)yox-1-1-2120.5y=-f(x)(3)y=f(|x|);(4)y=|f(x)|. 练习：已知函数y=f(x)的图象如图所，分别画出下列函数的图象：yox1-1-212-0.5(1)y=f(-x);(2)y=-f(x).(3)y=f(|x|);(4)y=|f(x)|.yox1-1-212-0.5yox1-1-212-0.5y=f(|x|)y=|f(x)| 例1.将函数y=2-2x的图象向左平移1个单位，再作关于原点对称的图形后.求所得图象对应的函数解析式.y=2-2xy=2-2(x+1)-y=2-2(-x+1)y=-22x-2向左平移1个单位关于原点对称x换成-xy换成-yx换成x+1 例2.已知函数y=|2x-2|（1）作出函数的图象；（2）指出函数的单调区间；（3）指出x取何值时，函数有最值。Oxy3211-1y=2xy=2x-2y=|2x-2|y=|2x-2| 例2.已知函数y=|2x-2|（1）作出函数的图象；（2）指出函数的单调区间；（3）指出x取何值时，函数有最值。Oxy3211-1y=|2x-2| 1．函数f(x)＝ln|x－1|的图像大致是(　　)解析：函数f(x)＝ln|x－1|的图像是由函数g(x)＝ln|x|向右平移1个单位得到的，故选B.答案：B 答案：C 4．使log2(－x)＜x＋1成立的x的取值范围是(　　)A．(－1,0)B．[－1,0)C．(－2,0)D．[－2,0)解析：作出y＝log2(－x)，y＝x＋1的图像知满足条件的x∈(－1,0)．答案：A 易错点一对“平移”概念理解不深导致失误【自我诊断①】把函数y＝log2(－2x＋3)的图像向左平移1个单位长度得到函数__________的图像．解析：由题意，得所求函数解析式为y＝log2[－2(x＋1)＋3]＝log2(－2x＋1)．答案：y＝log2(－2x＋1) 易错点二判断图像的对称性失误【自我诊断②】设函数y＝f(x)的定义域为R，则函数y＝f(x－1)与y＝f(1－x)的图像关于(　　)A．直线y＝0对称B．直线x＝0对称C．直线y＝1对称D．直线x＝1对称 解析：方法一：设(x1，y1)是y＝f(x－1)图像上任意一点，则y1＝f(x1－1)，而f(x1－1)＝f[1－(2－x1)]，说明点(2－x1，y1)－定是函数y＝f(1－x)上的一点，而点(x1，y1)与点(2－x1，y1)关于直线x＝1对称，所以y＝f(x－1)的图像与y＝f(1－x)的图像关于直线x＝1对称，所以选D.方法二：函数y＝f(x)与y＝f(－x)的图像关于y轴对称，y＝f(1－x)＝f[－(x－1)]．把y＝f(x)与y＝f(－x)的图像同时都向右平移1个单位长度，就得到y＝f(x－1)与y＝f(1－x)的图像，对称轴y轴向右平移1个单位长度得直线x＝1，故选D. 方法三：(特殊值法)设f(x)＝x2，则f(x－1)＝(x－1)2，f(1－x)＝(x－1)2，由图可知(两图像重合)，函数f(x－1)和f(1－x)的图像关于直线x＝1对称，只有D正确．答案：D 题型二函数图像的识别【例2】函数y＝f(x)与函数y＝g(x)的图像分别如图①、②所示．则函数y＝f(x)·g(x)的图像可能是(　　) 解析：从f(x)、g(x)图像可知它们分别为偶函数、奇函数，故f(x)·g(x)是奇函数，排除B.由g(x)图像不过(0,0)得f(x)·g(x)图像也不过(0,0)，排除C、D.答案：A规律方法：注意从f(x)，g(x)的奇偶性、单调性等方面寻找f(x)·g(x)的图像特征． 【预测2】(1)已知函数y＝f(x)的图像如图①所示，y＝g(x)的图像如图②所示，则函数y＝f(x)·g(x)的图像可能是下图中的(　　) (2)将f(x)改为奇函数，g(x)也是奇函数，例如，f(x)、g(x)图像分别如图③、④所示，则f(x)·g(x)的图像为(　　) 解析：(1)f(x)，g(x)均为偶函数，则f(x)·g(x)为偶函数，可排除A、D.注意x＜0时图像变化趋势是“负—正—负”，故只能选C.(2)f(x)·g(x)为偶函数，可排除A、C、D，选B.答案：(1)C　(2)B (2)由题意，有C：y＝lg(x＋1)－2.因为C1与C关于原点对称，所以C1：y＝－lg(－x＋1)＋2.因为C2与C1关于直线y＝x对称(即两函数互为反函数)，故C2：y＝1－102－x(x∈R)． 规律方法：(1)化为同底数；(2)翻折、平移；(3)平移、对称、反函数；(4)平移、伸缩． 题型四函数图像的应用【例4】当x∈(1,2)时，不等式(x－1)2＜logax恒成立，求a的取值范围． 解析：设f1(x)＝(x－1)2，f2(x)＝logax，要使当x∈(1,2)时，不等式(x－1)2＜logax恒成立，只需f1(x)＝(x－1)2在(1,2)上的图像在f2(x)＝logax的下方即可．当0＜a＜1时，由图像知显然不成立．当a＞1时，如图，要使在(1,2)上，f1(x)＝(x－1)2的图像在f2(x)＝logax的下方，只需f1(2)≤f2(2)．即(2－1)2≤loga2，loga2≥1，∴1＜a≤2. 【预测4】已知函数f(x)＝|x2－4x＋3|.(1)求函数f(x)的单调区间；(2)求m的取值范围，使得方程f(x)＝mx有四个不等实根．f(x)的图像如图所示．函数f(x)的单调区间有(－∞，1]、[1,2]、[2,3]、[3，＋∞)，其中增区间有[1,2]、[3，＋∞)，减区间有(－∞，1]、[2,3]． 小结1.已学的画函数图像的基本方法（1）描点法；（2）图象变换法：平移变换、对称变换2.画函数图像时可先确定函数的定义域、讨论函数的性质（如单调性、奇偶性、特殊点等），再用描点法或图像变换得出图像 上海第二医科大学附属新华医院泌尿外科王伟明肾肿瘤 概述肾脏各部位都可发生肿瘤肾实质性肿瘤90%以上是恶性的来源于肾实质：肾（腺）癌（占85％）肾母细胞瘤（小儿恶性肿瘤20％）来源于尿路上皮：肾盂肿瘤 肾癌又称肾细胞癌、肾腺癌发病年龄50-60岁男：女＝2：1多数单侧，双侧1-2％ 病理(一)起源：肾小管上皮细胞无组织学包膜，可有假包膜典型切面呈均匀黄色或棕色但多数伴囊性出血、坏死透明细胞、颗粒细胞、梭形细胞 病理(二)转移途径1.局部扩散肾外：假包膜、肾包膜、肾周筋膜肾内：癌栓沿肾静脉→下腔静脉→右心房2.淋巴转移:先累及肾门淋巴结3.血行转移:肺、脑、骨、肝 临床表现(一)局部表现三大症状1.血尿：间歇性无痛性肉眼血尿提示肿瘤已侵犯肾盂肾盏2.腰痛：通常表现为钝痛，绞痛少见原因；肾包膜牵拉，侵犯邻近器官或腰肌3.肿块：光滑质硬无压痛、随呼吸运动 临床表现(二)肾外表现1.发热：很常见，多为低热，四联症2.高血压：血管受压、动静脉瘘、肿瘤分泌肾素增加3.血沉快：血沉快提示预后不良4.贫血：血尿、铁进入癌细胞5.肝功能异常 临床表现(三)6.免疫系统改变：神经肌肉、血管改变7.激素改变：红细胞增多、高血钙8.尿多胺升高9.血癌胚抗原升高10.精索静脉曲张：平卧不消退 诊断和鉴别诊断1.临床表现和体格检查2.KUB+IVU：肾影增大、肾盂肾盏受压3.B超：可发现1cm以上的实质性占位4.CT、MRI：小肿瘤、淋巴结、静脉癌栓5.选择性肾动脉造影：诊断/治疗6.鉴别诊断：肾错构瘤、肾囊肿 治疗1.手术治疗：为主要治疗手段肾癌根治术：包括：肿瘤肾、肾周脂肪、肾们淋巴结、同侧肾上腺2.放射治疗：疗效差，不用3.化学治疗：疗效差，配合免疫治疗4.免疫治疗；主要用于转移癌 肾母细胞瘤肾母细胞瘤（Nephroblastoma）是婴幼儿最常见的恶性实体瘤之一又名Wilms瘤，肾胚胎瘤发病率：3岁以内占75％男女及左右比例相当诊断时平均年龄15月 病理来源：胚胎性肾组织组份：腺体、肌肉、神经、脂肪、骨等大体观：鱼肉样、灰白色、可有囊性变或出血，与正常组织无界限，生长快转移：局部血行、淋巴转移 临床表现1.腹部肿块：虚弱婴幼儿腹部巨大包块为本病特点，95％以上在洗澡、穿衣时偶然发现。2.血尿：不明显，肉眼血尿10％3.高血压：肾素活性增高4.低热：肿瘤坏死5.红细胞增多 诊断1.病史：婴幼儿腹部进行性增大肿块，首先考虑肾母细胞瘤2.辅助检查：B超、KUB+IVP、CT、MRI鉴别诊断:肾上腺神经母细胞瘤巨大肾积水 治疗手术、放疗、化疗综合应用1.手术：经腹部肾切除术2.放疗；术前放疗6-8天，减少肿瘤体积，2周内手术3.化疗：常用长春新碱和更生霉素 肾盂肿瘤发病年龄：40-70岁，平均55岁男女比例：2：1 病理1.来源：肾盏肾盂的移行上皮细胞，移行上皮细胞癌最多，鳞状上皮和腺上皮少见2.大体观：80％呈乳头状，20％实体性3.转移：淋巴转移较早 临床表现1.间歇性无痛性肉眼血尿2.可有肾绞痛3.体征不明显 诊断1.病史2.尿脱落细胞学检查3.KUB+IVU：肾盂内充盈缺损需与血块、结石鉴别4.CT、MRI5.B超：须与血块鉴别6.输尿管镜 治疗1.手术治疗：肾盂癌根治术范围：肾、输尿管及输尿管膀胱开口部分内腔镜手术2.密切随访其余尿路上皮器官'