最新函数的奇偶性-PPT精品课件PPT课件.ppt 39页

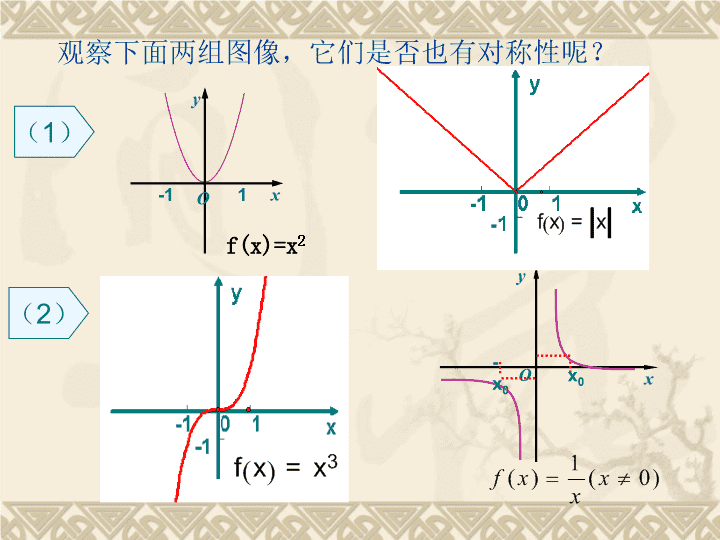
'函数的奇偶性-PPT精品课件 在日常生活中，有非常多的轴对称现象，如人与镜中的影关于镜面对称，请同学们举几个例子。除了轴对称外，有些是关于某点对称，如风扇的叶子，如图：它关于什么对称？而我们所学习的函数图像也有类似的对称现象，请看下面的函数图像。 观察下面两组图像，它们是否也有对称性呢？xyO1-1f(x)=x2（1）（2）yxOx0-x0 理解定义yox4-2思考？函数具有奇偶性的前提是什么？函数的定义域关于原点对称 对于奇、偶函数定义的几点说明:(2)定义域关于原点对称是函数具有奇偶性的先决条件。（3）奇、偶函数定义的逆命题也成立，即：若函数f(x)为奇函数,则f(-x)=－f(x)成立。若函数f(x)为偶函数,则f(-x)=f(x)成立。（1）如果一个函数f(x)是奇函数或偶函数,那么我们就是说函数f(x)具有奇偶性。 在线测试1、对于定义在R上的函数f(x)，下列判断是否正确？（1）若f(x)是偶函数，则f(-2)=f(2)()（2）若f(-2)=f(2)，则函数f(x)是偶函数（）（3）若f(-2)≠f(2)，则函数f(x)不是偶函数（）2、已知函数f(x)是偶函数，且f（3）=3，则f(-3)=（）A、-3B、3C、0D、无法确定3、下列四个结论：偶函数的图像一定与y轴相交；奇函数的图像一定过原点；偶函数的图像关于y轴对称；奇函数y=f(x)(x)的图像必过（-a,f(a)）表述正确的个数是A、1B、2C、3D、4 4、已知函数f(x)是奇函数，且f(3)=3，则f(-3)等于（）A、-3B、3C、0D、无法确定5、已知函数f(x)=x3，-5≤x<5，则下列结论正确的是（）（A）函数f(x)是奇函数（B）函数f(x)的图像关于原点中心对称（C）函数定义域中由无数多个x，使得f(-x)=-f(x)（D）函数f(x)的定义域是关于原点对称的区域 思考：如何判断一个函数的奇偶性呢？（1）图像法（2）定义法 例1.根据下列函数图象,判断函数奇偶性.yxyxyxyxy典例详解 xoy(a,f(a))(-a,f(-a))-aa奇函数的图象关于原点对称，反过来，如果一个函数的图象关于原点对称，那么这个函数是奇函数. xoy-aa(a,f(a))(-a,f(-a))偶函数的图象关于y轴对称，反过来，如果一个函数的图象关于y轴对称，那么这个函数是偶函数. oyx例2已知函数y=f(x)是偶函数，它在y轴右边的图象如图，画出y=f(x)在y轴左边的图象。 第一课时【互动探究案】例2、已知函数y=f(x)是偶函数，且知道x≥0是的图像，请作出另一半图象。yx练习 例3.判断下列函数的奇偶性(1)f(x)=x3+x(2)f(x)=3x4+6x2+a解:定义域为R∵f(-x)=(-x)3+(-x)=-x3-x=-(x3+x)即f(-x)=-f(x)∴f(x)为奇函数解:定义域为R∵f(-x)=3(-x)4+6(-x)2+a=3x4+6x2+a即f(-x)=f(x)∴f(x)为偶函数说明：用定义判断函数奇偶性的步骤:⑴先求出定义域，看定义域是否关于原点对称.⑵再判断f(－x)=-f(x)或f(-x)=f(x)是否成立. 用定义法判断函数奇偶性解题步骤:(1)先确定函数定义域,并判断定义域是否关于原点对称;(2)求f(-x)，找f(x)与f(-x)的关系;若f(-x)=f(x),则f(x)是偶函数;若f(-x)=-f(x),则f(x)是奇函数.(3)作出结论.f(x)是偶函数或奇函数或非奇非偶函数或即是奇函数又是偶函数。给出函数判断定义域是否对称结论是f(-x)与f(x)否 练习:说出下列函数的奇偶性:①f(x)=x4________③f(x)=x________④f(x)=x-2__________⑤f(x)=x5__________⑥f(x)=x-3_______________②f(x)=x-1__________奇函数奇函数奇函数奇函数偶函数偶函数对于形如f(x)=xn()的函数，在定义域R内:若n为偶数，则它为偶函数。若n为奇数，则它为奇函数。 思考1：函数f(x)=2x+1是奇函数吗？是偶函数吗？xy012f(x)=2x+1-1分析：函数的定义域为R但是f(-x)=2(-x)+1=-2x+1∴f(-x)≠-f(x)且f(-x)≠f(x)∴f(x)既不是奇函数也不是偶函数。（也称为非奇非偶函数）如右图所示：图像既不关于原点对称也不关于y轴对称。 (1)f(x)=(2)f(x)=x2x∈[-4,4)解:∵定义域不关于原点对称或∵f(-4)=(-4)2=16;f(4)在定义域里没有意义.∴f(x)为非奇非偶函数解:定义域为[0,+∞)∵定义域不关于原点对称∴f(x)为非奇非偶函数思考2：以下两个函数是奇函数吗？是偶函数吗？ 思考3：在前面的几个函数中有的是奇函数，有的是偶函数，也有非奇非偶函数。那么有没有这样的函数，它既是奇函数又是偶函数呢？有。例如：函数f(x)=0是不是只有这一个呢？若不是，请举例说明。xy01f(x)=0-1 奇函数偶函数既奇又偶函数非奇非偶函数根据奇偶性,函数可划分为四类: 课堂小结1奇偶性定义:对于函数f(x),在它的定义域内，①若有f(-x)=-f(x),则f(x)叫做奇函数；②若有f(-x)=f(x),则f(x)叫做偶函数。2图象性质:奇函数的图象关于原点对称;偶函数的图象关于y轴对称.3判断奇偶性方法：图象法，定义法。4定义域关于原点对称是函数具有奇偶性的前提 半夏厚朴汤《金匮要略》 组成：半夏—升15克厚朴三两9克茯苓四两12克生姜五两9克苏叶二两6克用法：上五味，以水七升，煮取四升，分温四服，日三夜一服。主治：痰气郁结之梅核气。病机：七情郁结兼中上二焦寒痰停饮。治法：行气解郁、降逆化痰。 主治—梅核气原文：“妇人咽中如有炙脔，半夏厚朴汤主之”。辨证要点：该方为治疗情志不畅，痰气互结所致的梅核气之常用方。临床应用以咽中如有物阻，吞吐不得，胸膈满闷，苔白腻，脉弦滑为辨证要点。 主证病机分析痰气互结于咽喉：咽中如有物阻，咯咳不出，吞咽不下，苔白腻，脉弦滑肺胃气机不畅：胸膈满闷，或咳或呕七情郁结痰气凝滞 半夏（君药）化痰散结，降逆和胃厚朴（臣药）下气除满，散结降逆茯苓渗湿健脾助半夏化痰半夏生姜（佐药）辛温散结，和胃止制半夏毒苏叶芳香行气，理肺舒肝助厚朴行气厚朴宽胸、宣通郁结之气*配伍要点：厚朴+半夏厚朴配半夏,一行气滞,一化痰结,以达行气化痰散之功。 配伍特点半夏厚朴汤属于表里双解、温散水饮之方剂。生姜、苏叶辛温发散，半夏辛温散结，厚朴辛温苦降，全方含“辛开苦降”开郁散结之义。方中茯苓，渗湿利痰，其性先升后降。除茯苓甘、淡、平外，其余诸药皆具辛温之性，符合张仲景“病痰饮者当以温药和之”的用药原则。 配伍特点方中所用辛温之药皆归肺、脾经，主要治疗中、上二焦寒痰流饮气郁诸病。本方也可从三焦辨证的角度进行分析:上焦苏叶辛宣芳化，中焦半夏、厚朴、生姜辛开苦降，下焦茯苓淡渗利水。所治部位涉及上、中、下三焦，病机为气郁、湿滞、痰阻。 使用注意1、方中多辛温苦燥之品，仅适宜于痰气互结而无热者。2、若见颧红口苦、舌红少苔属于气郁化火，阴伤津少者，虽具梅核气之特征，亦不宜使用本方。 运用——临证加减（1）呃逆，属肝气犯胃，气逆痰阻者，本方加柴胡、白芍、青皮，以增强舒肝解郁之力。恶阻，属脾胃虚弱，聚湿生痰，痰随冲气上逆者，方加白术、红人参，取其补益脾胃之力，以除痰湿之源。风寒咳喘，本方加麻黄、杏仁、苏子易苏叶，以止咳平喘。泄泻，属寒湿者，加苍术、藿香之芳香以化浊，以使寒湿解除。 运用——临证加减（2）奔豚气，属肝气郁结，寒气上逆而作奔豚，本方加桂枝以温经散寒。气机郁滞甚者，加柴胡、郁金、川楝子、香附、青皮，疏肝理气之味，亦可合逍遥散加减。气郁重于痰湿者，本方加大枣，名四七汤。[和济局方]呕吐较重者，本方加重半夏、生姜之量，或加砂仁、白豆蔻、丁香，以降气止呕。梅核气，本方加苏梗、白梅花、香附、郁金，以疏肝理气化痰。 新药研制提要梅核气因情志不遂诱发，多兼见咽喉不利，新药研制时，可合四逆散疏肝理脾，加贝浙母和桔梗祛痰利咽。 现代应用本方常用于癔病、胃神经官能症、慢性咽炎、慢性支气管炎、食道痉挛等属气滞痰阻者。 谢谢大家~第四组成员;黄镝，李莉思，林雄，喻玄，肖辅，刘晓茜，祝蕾，陈曦文，刘青霞'