最新机械设计基础PPT课件-第12章蜗轮蜗杆课件PPT.ppt 88页

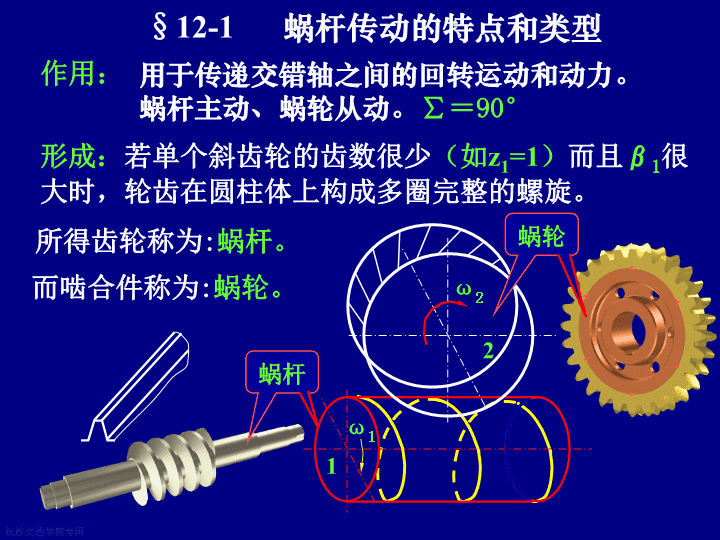
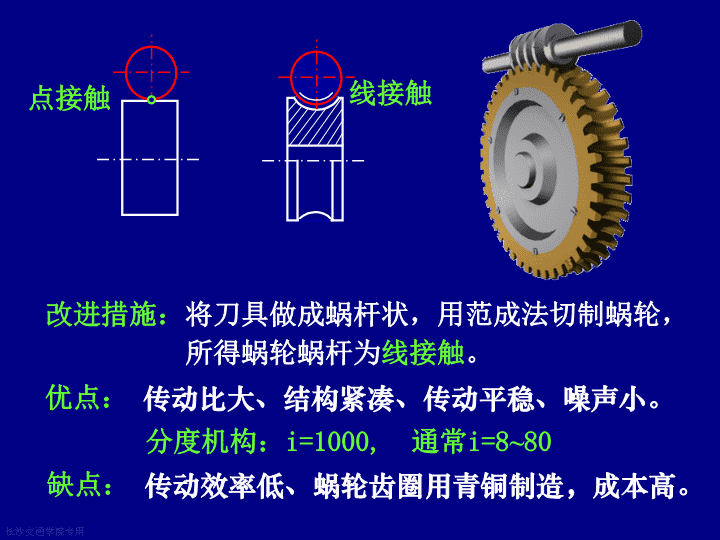
'机械设计基础PPT课件-第12章蜗轮蜗杆 §12-1蜗杆传动的特点和类型作用：用于传递交错轴之间的回转运动和动力。蜗杆主动、蜗轮从动。∑＝90°形成：若单个斜齿轮的齿数很少（如z1=1）而且β1很大时，轮齿在圆柱体上构成多圈完整的螺旋。1ω1所得齿轮称为:蜗杆。而啮合件称为:蜗轮。蜗杆2ω2蜗轮长沙交通学院专用 改进措施：将刀具做成蜗杆状，用范成法切制蜗轮，所得蜗轮蜗杆为线接触。点接触优点：传动比大、结构紧凑、传动平稳、噪声小。分度机构：i=1000,通常i=8~80缺点：传动效率低、蜗轮齿圈用青铜制造，成本高。线接触长沙交通学院专用 压力角:α=20°模数m取标准值，与齿轮模数系列不同。分度传动，推荐用α=15°动力传动，推荐：α=25°第一系列1,1.25,1.6,2,2.5,3.15,4,5,6.3810,12.5,16,20,25,31.5,40第二系列1.5,3,3.5,4.5,5.56,7,12,14蜗杆模数m值GB10088-882.模数m和压力角α长沙交通学院专用 为了减少加工蜗轮滚刀的数量，规定d1只能取标准值。蜗轮蜗杆轮齿旋向相同.若∑＝90°∴γ1＝β2ttβ2β1∵γ1+β1＝90°蜗轮右旋蜗杆右旋＝β1+β2β1γ1d1s=e的圆柱称为蜗杆的分度圆柱。esd2∑长沙交通学院专用 表12－1蜗杆分度圆直径与其模数的匹配标准系列mmm11.251.62d1182022.42028(18)22.4(28)35.5m2.53.154d1(22.4)28(35.5)45(28)35.5(45)56(31.5)m456.3d140(50)71(40)50(63)90(50)63m6.3810d1(80)112(63)80(100)140(71)90…摘自GB10085-88,括号中的数字尽可能不采用长沙交通学院专用 3.传动比i、蜗杆头数z1和蜗轮齿数z2蜗杆头数z1：即螺旋线的数目。d蜗杆转动一圈，相当于齿条移动z1个齿，推动蜗轮转过z1个齿。传动比:z1z2=---n2n1i=---通常：z1=1~4若想得到大i,可取：z1=1，但传动效率低。对于大功率传动,可取：z1=2，或4。蜗轮齿数：z2=iz1为避免根切：z2≥26一般情况：z2≤80z2过大→→蜗杆长度↑→刚度、啮合精度↓结构尺寸↑长沙交通学院专用 表12-2蜗杆头数z1与蜗轮齿数z2的推荐值传动比i7~1314~2728~40>40蜗杆头数z1422、11蜗轮齿数z228~5228~5428~80>40将分度圆柱展开得：=z1px1/πd1=mz1/d1tgγ1=l/πd14.蜗杆的导程角γπd1lpx1γ1d1γ1β1长沙交通学院专用 5.蜗杆直径系数q加工时滚刀直径等参数与蜗杆分度圆直径等参数相同，为了限制滚刀的数量，国标规定分度圆直径只能取标准值，并与模数相配。q为蜗杆:定义：q=d1/m一般取:q=8～18。tgγ1=pxz1/πd1=z1/q于是有：d1=mq可由表12－1计算得到。直径系数见下页=mz1/d1长沙交通学院专用 m11.251.62d1182022.42028(18)22.4(28)35.5m2.53.154d1(22.4)28(35.5)45(28)35.5(45)56(31.5)m456.3d140(50)71(40)50(63)90(50)63m6.3810d1(80)112(63)80(100)140(71)90…表12－1蜗杆分度圆直径与其模数的匹配标准系列mm20q=12.528q=17.51.6长沙交通学院专用 ω11p212p由相对运动原理可知:v2=v1+vS6.齿面间滑动速度vS及蜗轮转向的确定=v1/cosγvS=v22+v12作速度向量图，得:v2=v1tgγγ蜗轮的转向:v2ω2ω2CWttγv1v2vS长沙交通学院专用 ω1ω112p12p右旋蜗杆：伸出左手，四指顺蜗杆转向，则蜗轮的切向速度vp2的方向与拇指指向相同。用手势确定蜗轮的转向：左旋蜗杆：用右手判断，方法一样。ω2ω2v2v2蜗轮的转向因蜗轮蜗杆相当于螺旋副的运动，有一种实用且简便的转向判别方法：7.中心距a=r1+r2=m(z2+q)/2ar1r2长沙交通学院专用 二、圆柱蜗杆传动几何尺寸的计算由蜗杆传动的功用，以及给定的传动比i,→z1→z2→计算求得m、d1→计算几何尺寸表12-3普通圆柱蜗杆传动的几何尺寸计算名称计算公式蜗杆中圆直径，蜗轮分度圆直径齿顶高齿根高顶圆直径根圆直径蜗杆轴向齿距、蜗轮端面齿距径向间隙中心距蜗杆蜗轮d1=mqd2=mz2ha=mha=mdf=1.2mqdf=1.2mqda1=m(q+2)da1=m(q+2)df1=m(q-2.4)df2=m(q-2.4)pa1=pt2=px=πmc=0.2ma=0.5(d1+d2)m=0.5m(q+z2)长沙交通学院专用 §12-3蜗杆传动的失效形式、材料和结构一、蜗杆传动的失效形式及材料选择主要失效形式：胶合、点蚀、磨损。材料蜗轮齿圈采用青铜：减摩、耐磨性、抗胶合。蜗杆采用碳素钢与合金钢：表面光洁、硬度高。材料牌号选择：高速重载蜗杆：20Cr,20CrMnTi(渗碳淬火56~62HRC)或40Cr42SiMn45(表面淬火45~55HRC)一般蜗杆：4045钢调质处理(硬度为220~250HBS)蜗轮材料：vS>12m/s时→ZCuSn10P1锡青铜制造。vS<12m/s时→ZCuSn5Pb5Zn5锡青铜vS≤6m/s时→ZCuAl10Fe3铝青铜。vS<2m/s时→球墨铸铁、灰铸铁。长沙交通学院专用 二、蜗杆蜗轮的结构蜗杆通常与轴制成一体z1=1或2时：b1≥(11+0.06z2)mz1=4时:b1≥(12.5+0.09z2)mb1→蜗杆轴蜗杆长度b1的确定：长沙交通学院专用 蜗轮齿宽角θ90~130˚轮圈厚度C≈1.6m+1.5mm轮缘宽度B≤0.75da0.67da蜗轮顶圆直径de2≤da2+2mda2+1.5mda2+2m蜗杆头数Z1124蜗轮的常用结构：整体式组合式过盈配合θθθθde2de2de2de2BBBBccc组合式螺栓联接组合式铸造骑缝螺钉4~8个，孔心向硬边偏移δ=2~3mmδ长沙交通学院专用 §12-4圆柱蜗杆传动的受力分析Ft2Fr2Fa2Ft1Fr1Fa1ω2法向力可分解为三个分力：圆周力：Ft轴向力：Fa径向力：Fr且有如下关系：Ft1=Fa2Fr1=Fr2Fa1=Ft2=2T1/d1=2T2/d2=Ft2tgα式中：T1、T1分别为作用在蜗杆与蜗轮上的扭矩。T2=T1iηω2α长沙交通学院专用 §12-5圆柱蜗杆传动的强度计算齿面接触强度验算公式：d1d22KT2σH=500m2d1z22KT2=500≤[σH]由上式可得设计公式：m2d1≥KT2z2[σH]5002式中K为载荷系数，取：K=1.1~1.3m、d1应选取标准值确定。蜗轮齿面的接触强度计算与斜齿轮相似，仍以赫兹公式为基础。以蜗轮蜗杆的节点处啮合相应参数代入即可。赫兹公式:长沙交通学院专用 表12－1蜗杆分度圆直径与其模数的匹配标准系列mmm11.21.62d1182022.42028(18)22.4(28)35.5m2.53.154d1(22.4)28(35.5)45(28)35.5(45)56(31.5)m456.3d140(50)71(40)50(63)90(50)63m6.3810d1(80)112(63)80(100)140(71)90…摘自GB10085-88,括号中的数字尽可能不采用长沙交通学院专用 表12-4锡青铜蜗轮的许用接触应力[σH]蜗轮材料铸造方法适用的滑动速度蜗杆齿面硬度ZQSn10-1ZQSn5-5-5砂型≤12180200金属型≤12135150Vsm/sHBS≤350HRC≥45金属型≤25200220砂型≤10110125当蜗轮采用青铜制造时，蜗轮的损坏形式主要是疲劳点蚀，其许用的接触应力如下表：长沙交通学院专用 当蜗轮采用无锡青铜或铸铁制造时，蜗轮的损坏形式主要是胶合。其许用的接触应力应根据材料组合和滑动速度来确定。表12-5铝青铜及铸铁蜗轮的许用接触应力[σH]Mpa蜗轮材料蜗杆材料滑动速度vsm/sZQAl10-3HT150淬火钢*渗碳钢调质钢0.52501301101230115902109070180——160——120——2346890——*蜗杆未经淬火时需将表中[σH]值降低20%。HT150、HT200长沙交通学院专用 §12-6蜗杆传动的效率、润滑和热平衡计算一、圆柱蜗杆传动的效率功率损耗：啮合损耗、轴承摩擦损耗、搅油损耗。η=（0.95~0.97）tg(γ+ρ’)tgγ蜗杆主动时，总效率计算公式为：式中:γ为蜗杆导程角;ρ’称为当量摩擦角，ρ’=arctgf’,f’为当量摩擦系数，取值见表12-6,P190详见下页长沙交通学院专用 表12-6当量摩擦系数和当量摩擦角蜗轮材料锡青铜无锡青铜蜗杆齿面硬度HRC>45其他情况HRC>45滑动速度vsm/sf’ρ’f’ρ’f’ρ’0.010.116.28˚0.126.84˚0.1810.2˚0.100.084.57˚0.095.14˚0.137.4˚0.500.0553.15˚0.0653.72˚0.095.14˚1.000.0452.58˚0.0553.15˚0.074˚2.000.0352˚0.0452.58˚0.0553.15˚3.000.0281.6˚0.0352˚0.0452.58˚4.000.0241.37˚0.0311.78˚0.042.29˚5.000.0221.26˚0.0291.66˚0.0352˚8.000.0181.03˚0.0261.49˚0.031.72˚10.00.0160.92˚0.0241.37˚15.00.0140.8˚0.0201.15˚24.00.0130.74˚长沙交通学院专用 γ↑→η↑→对动力传动，宜采用多头蜗杆→蜗杆加工困难γ过大当γ>28˚时，效率η增加很少。当γ≤ρ’时，蜗杆具有自锁性，但效率η很低。<50%η=（0.95~0.97）tg(γ+ρ’)tgγ分析：上述公式不直观，工程上常用以下估计值。闭式传动：z1=1η=0.70~0.75z1=2η=0.75~0.82z1=4η=0.87~0.92z1=1、2η=0.60~0.70开式传动：长沙交通学院专用 二、蜗杆传动的润滑若润滑不良，→效率显著降低↓→早期胶合或磨损润滑对蜗杆传动而言，至关重要。润滑油粘度的选择：表11-5齿轮传动润滑油粘度荐用值塑料、铸铁、青铜齿轮材料强度极限圆周速度v(m/s)运动粘度v/cSt（40℃）渗碳或表面淬火钢钢3505~12.512.5~25>252.5~51~2.50.5~1<0.52201501008055450~10001000~12501250~1580500350220150100805005003502201501009005005003502201505580100长沙交通学院专用 润滑方式的选择：当vs≤5~10m/s时，采用油池浸油润滑。为了减少搅油损失，下置式蜗杆不宜浸油过深。当vs>10~15m/s时，采用压力喷油润滑。当v1>4m/s时，采用蜗杆在上的结构。长沙交通学院专用 三、蜗杆传动的热平衡计算由于蜗杆传动效率低，发热量大，若不及时散热，会引起箱体内，油温升高，润滑失效，导致轮齿磨损加剧，甚至出现胶合。因此，对连续工作的闭式蜗杆传动必须进行热平衡计算对闭式传动，热量由箱体散逸，要求箱体与环境温差：∆t=αiA1000P1(1-η)tgγ≤[∆t]∆t=(t-t0)----温度差；P1----蜗杆传递的功率；αi----表面散热系数；一般取：αi=10~17W/(m2℃)A----散热面积,m2,指箱体外壁与空气接触而内壁被油飞溅到的箱壳面积。对于箱体上的散热片，其散热面积按50%计算。长沙交通学院专用 [∆t]----温差许用值，一般取：[∆t]=60~70℃要求油温：t=t0+∆t<90℃不能满足要求时，可采取冷却措施：1）增加散热面积----加散热片；2）提高表面传热系数----加风扇、冷却水管、循环油冷却。油泵冷却器冷却水长沙交通学院专用 本章重点(1) 熟悉蜗杆传动的特点。(2) 了解蜗杆传动的类型、应用、材料和结构。(3) 掌握普通圆柱蜗杆的主要参数和几何尺寸计算。长沙交通学院专用 第四章程序语言的性质33 语言的形式化模型BNF为描述程序设计语言的属性提供了一种很好的手段，但并不是充分的手段。BNF回答了程序看起来象什么，但没有回答程序是做什么的。形式化模型采用精确的数学模型来刻画研究对象，为研究、分析和操纵研究对象提供严谨的数学工具和手段。本章将介绍下列形式化模型：形式文法：乔姆斯基文法分级语言的语义：属性文法、指称语义程序的验证34 4.1语言的形式化性质乔姆斯基分级文法语言的能力35 乔姆斯基分级文法文法由非终结符、终结符、开始（非终结）符、及产生式构成文法的类别3型文法：正则文法，定义词法的模型2型文法：BNF文法，上下文无关文法1型文法：上下文有关文法0型文法：36 3型文法：正则文法为词法分析器提供模型。这类文法的大多数性质都是可判定的如，能产生什么样的串、给定串是否属于文法规定的语言、语言中的串是否有限等正则文法可以产生形如an的串，其中a为有限字符序列正则文法只能计数有限数常用于关键字或单词扫描37 2型文法—上下文无关文法产生式的形式为：X,其中可以是终结符和非终结符的任意序列同样，这类文法的大多数性质都是可判定的如，能产生什么样的串、给定串是否属于文法规定的语言、语言是否为空等可用来计数和比较两个项，产生形如ancbn的串可以用堆栈来实现可用来自动产生程序的语法分析树2型和3型文法的相关问题都已基本上得到解决38 1型文法—上下文有关文法产生式的形式为：,其中任意非终结符串，是终结符和非终结符的任意序列，但中的符号个数应不多于的符号个数从开始符开始导出的串的长度是递增的在生成串时，需要使用固定数量的存储空间，例如识别上下文无关文法无法识别的串ancnbn上下文有关文法太复杂，很难用于程序设计语言人们对上下文有关文法的很多特征还不太清楚39 0型文法—非限定型文法对产生式的形式没有任何限制可用来识别任意可计算的函数其大多数性质都是不可判定的返回40 不可判定性不同类型的文法越来越复杂，产生的语言也越来越复杂，但是否说明计算机解决问题的能力可以越来越强，没有限制？例如：能否编写一个C语言程序来判断另一个C语言程序能否结束？但这基本上是不可能的，这不是编程人员的问题，而是因为计算机所基于的数学模型本身的局限性而导致的。41 图灵机一般来说，用一种语言编写的程序也可以用其他另一种语言来实现。那么是否存在某个程序，只能用某种语言来实现，而用其他语言就无法实现？如果没有，那么有哪些程序是其它程序设计语言无法表示的，为什么还需要那么多种不同的语言？如果我们将能够表示所有计算的语言都称为通用语言，那么是不是所有语言都是通用语言？如果是，是否存在更简单的通用语言？42 图灵机的结构图灵机是一种用来定义可计算函数的抽象计算机图灵机只有一个单一的数据结构，即一个称为“带子”的可变长线性数组带子被分为很多格，每格上只包含一个字符图灵机还有一个指针变量，称为“读出头”，它总是指向带子上的某个格。43 图灵机的操作图灵机只提供几个简单的操作：读出头所指定位置的字符可以被读出或被修改。程序可以根据读出的值进行转移。读出头可以左右移动。如果读出头移动到带子的最末端，则自动在带子上加上一格，并赋予一个空字符作为初始值。44 图灵机的运行图灵机开始运行时，带子上存放输入数据，读出头指向输入数据的最左端的字符；图灵机根据预先编好的操作序列读写带子上的数据、或移动读出头；如果最终能够停机，则带子上的内容就是最后的输出结果。45 图灵机的能力任意可计算函数都可以用图灵机计算出来（Church论题）图灵机等价于0型文法确定型图灵机等价于非确定型图灵机。46 停机问题是否存在某个通用的算法，它能够断定任意给定的图灵机在任意的输入下能否停机？停机问题是不可判断的，即不存在这样的通用算法。任意一个不可判断的问题，都等价于停机问题。结论：任何一种程序设计语言都可能代替其它语言程序设计语言不存在质的区别，只有量的区别，如是否优美、易用、高效等任何一种程序设计语言都有它存在的理由返回47 4.2语言的语义程序设计语言基本上都是以上下文无关文法(特别是LR(k)文法)的核心设计的。但语法分析已经不再是人们感兴趣的研究问题了。现在的问题是如何确定程序的含义（即语义）。48 语言的语义语言的手册必须定义语言中每个结构的含义，包括单独结构的含义以及和其他结构组合时的含义。语言提供了不同结构，用户（为了写正确的程序，预测语句的执行效果）和实现者（正确地实现语言）需要这些结构的精确定义。大多数语言中，形式文法用于定义语法，一段文字或例子用于定义语义，但定义是不精确的，有二义性，不同作者可能有不同理解。语义定义问题还是理论研究的目标，但至今没有令人满意的解答。已有各种形式方法用于语义定义。49 语义建模（1）—文法模型对定义语言的BNF文法进行扩展，给出程序的语法分析树，从树中抽取出附加信息。属性文法便是抽取附加信息的一种方式。50 语义建模（2）—命令或操作模型定义程序如何在某虚拟机上执行。通常描述为一自动机，但比语法用的简单自动机远为复杂。自动机有内部状态——对应程序执行时的内部状态，包括所有变量的值、执行程序本身、以及各种系统定义的数据结构。51 语义建模（2）—命令或操作模型一组形式定义的操作用于刻划自动机内部状态如何改变。此外还需定义程序文本如何翻译成自动机的初始状态。语言的操作定义对语言如何实际执行给出了相当直接的抽象。也可能提出一个更抽象的模型，作为语言的软件解释的基础。70年代的VDL（ViennaDefinitionLanguage）是一个操作方法。它扩展语法分析树已包含机器解释器。计算的状态是程序树加上描述机器中所有数据的树。每条语句的执行使树的状态发生变化。52 语义建模（3）—作用型模型试图直接构造每个程序的函数的定义，采用层次式的构造方式。程序中每个基本的或程序员定义的操作代表一个数学函数。语言的程序控制结构用于将这些函数复合为更大的序列，代表表达式和语言。语句序列和条件分叉表示为个体函数构造而成的函数。循环通常表示为递归函数。最终，为整个程序导出一个完整的函数模型，指称语义归于此类。53 语义建模（4）—公理模型使用谓词演算，每个语法结构的语义被描述为公理或推导规则，用于导出结构的执行效果。从一个初始假设开始，假设输入变量满足一定的约束，在程序语句执行后，使用公理和推导规则来推导其他变量值需满足的限制，最终，程序的结果被证明满足希望的约束（描述了它们的值和输入值的关系）。如Hoare的公理语义。54 语义建模（5）—规约模型描述实现程序的各个函数的关系，只要我们可以证明一个实现符合了所有的函数间的关系，则称实现相对于规约是正确的。代数数据类型是形式规约的一种形式。例如：实现栈的程序，S表示栈，则有公理，pop(push(S,x))=S任何一个实现如果能保持这种关系，则称是栈的正确实现。55 语义模型—小结上述各种形式语义模型各有优点，但均不能称为完全实用的和适用的，各有其适合范围。操作语义为语言的实现提供了一种形式模型，但对用户来说太细节公理语义易于理解，但很难用来定义复杂的程序设计语言，且缺乏对语言实现的支持返回56 语义建模—属性文法这是最早的开发语义模型的工作之一。其思想是对分析树中的每个结点关联一个函数，从而给出结点的语义内容。属性文法的创建过程是为文法中的每一条规则都定义相关的语义函数。继承属性是一个函数，它将树中非终结符值和树中更高层的非终结符值相关联。换言之，任何规则右端的非终结符的函数值是左端非终结符的函数。综合属性是一个函数，它将左端非终结符和右端非终结符的值相关联，这些属性在树中向上传递信息，即从树中下层信息进行“综合”。57 属性文法例：考虑算术表达式的简单文法。E→T|E+TT→P|T×PP→I|(E)其语义通过文法中非终结符间的关系集合定义。如：下面函数生成该文法生成的任意表达式的值：产生式属性E→E+TValue(E1)=V(E2)+V(T)E→TV(E)=V(T)T→T×PV(T1)=V(T2)×V(P)T→PV(T)=V(P)P→IV(P)=数I的值P→(E)V（P）=V（E）58 属性文法下图是一个属性树，它给出了表达式2+4×(1+2)值59 属性文法属性文法可用于在语法树中传递语义信息。例如，声明信息可以通过语言的声明产生式收集。沿树向下传的符号表信息可用于生成表达式代码。下面属性可加到非终结符和来创建一个程序中声明的名字集合。产生式属性::=decl_set(declaration1)=declaname(decl)∪decl_set(declaration2)::=decl_set(declaration)=decl-name(decl)::=declarexdecl-name(decl)=x(decl)::=declareydecl-name(decl)=y(decl)::=declarezdecl-name(decl)=z这是综合属性，包含程序中声明的名字集合。该属性可以沿树向下传递，成为继承属性，用于正确地生成数据的代码。60 属性文法的使用首先创建语法分析树。属性文法假设你已经知道表达式是如何推导出来的，它并不关心是如何分析推导出来的。定义属性的函数可以是任意给定的，因此定义属性的过程完全是手工完成的。如果只有综合属性，并且文法是LR(k)，那么，属性文法可以用来在语法分析时自动产程中间代码。这就是YACC如何工作的，它利用属性文法来计算所有非终结符的值。在构造分析树时，非终结符的信息逐层向上传递给分析树上层的非终结符。语法分析完毕，所有属性的值将计算出来。返回61 指称语义指称语义是一种用来描述程序设计语言的语义的作用型语义模型指称语义基于-演算62 -演算-演算是一种和图灵机的计算能力相当的理论计算模型-演算可以作为程序设计语言的函数调用的模型Algol和Lisp都采用来-演算的函数调用语义指称语义是对-演算的扩充，它将-演算扩充为一种通用的数据类型理论63 -演算的表达式-表达式可以递归地定义如下：变量名为-表达式如果M为一个-表达式，则x.M也是一个-表达式如果F和A都是-表达式，则(FA)也是-表达式，其中F为操作符，A为操作数。形式语法：-expr::=id|id.-expr|(-expr-expr)x相当于申明参数变量x，没有申明的变量为自由变量，否则为约束变量。x.M相当于函数申明，其中x相当于M的参数。例如：xx.xx.(xy)x.y(x.xy.y)64 -表达式的操作-表达式只有一种操作：约简(FA)约简相当于将A作为实际参数，替换F的形式参数的所有出现(x.MA)M’，相当于用A替换M中x的所有自由出现。例如：(x.xy)y(x.(xy)x.x)x.xyy注意：约简并不一定能简化原来的表达式(x.(xx)x.(xx))(x.(xx)x.(xx))……65 指称语义指称语义的基本思想是定义一个语义函数（指称函数），把程序的意义映射到某种意义清晰的数学对象（就像用中文解释英文）作为被指的数学对象可以根据需要选择对于简单的程序语言，一种很自然的选择是把程序的语义定义为（指称为）从状态到状态的函数。定义语义就是定义好每个程序对应的函数。程序的状态由标识符到值的映射集合构成S={id|value,…}66 指称语义表达式的语义[e]Sval语句的语义[s]SS程序的语义[m]valval67 指称语义设为程序的当前状态表达式的语义常数：[n]=n变量：[x]=(x)算术表达式：[e1+e2]=[e1]+[e2]语句的语义赋值语句：[x=e]={x|[e]}复合语句：[s1;s2]=[s2]([s1])条件语句：[ifbthens1elses2]=if[b]then[s1]else[s2]程序的语义[m]valval返回68 程序验证在编程时，人们越来越关心程序的正确性和可靠性。人们在设计程序设计语言时，也希望通过增加新的特征来增强程序的正确性和可靠性。我们可以用程序语义，按以下方式来探讨程序的正确性问题：给定程序P，其含义是什么？即，它的规范描述S是什么？给定规范描述S，开发实现了该规范描述的程序P规范描述S和程序P是否完成了相同的功能（执行了相同的函数）？相当于语义建模问题软件工程的核心问题程序验证的核心问题69 程序验证测试不能保证程序的正确性如果能找到不依赖于测试的保证程序正确性的方法，产生的程序就能更加可靠：程序计算了一个函数如果能给出该函数的规范描述，并且能够根据程序知道它到底计算了一个什么样的函数，那么，如果能够证明程序所计算的函数与给定的函数等价或相同，就能证明程序的正确性，而不需再测试。70 形式化的规范描述任一程序都可以表示成流程图基调：函数名：定义域值域fun1:S1andP1S3fun2:S1andnot(P1)S3fun3:S3andnot(P3)S4fun4:S3andP3S4S2andP2=S4S2andnot(P2)=S3P1P2P3Fcn1Fcn4Fcn3Fcn2S1S2S3S471 形式化的规范描述（续）这样，程序可以看成是一个定义在其基本成分上的复杂函数：C(fun1,fun2,fun3,fun4,p1,p2,p3):S1S4如果我们能够形式化地推导出上述关系，那么我们就能够从数学上证明，给定S1,程序将终止于状态S4。但是：证明非常困难。另外，在证明时，我们总是想证明程序和某个给定的形式化规范等价，但问题是，如果没有给出规范描述，“程序是否正确？”可能就没有了意义。72 公理化验证用谓词逻辑公式来刻画程序的语义、用谓词演算来验证程序的正确性。TonyHoare在1969年提出的。每个程序都遵循某种形式化的公理定义。实证（Validation）:通过一系列测试数据的测试，展示程序满足了其规范描述。验证（Verification）:根据程序结构，通过形式化的讨论，展示程序满足了其规范描述。Validation一般认为需要执行程序，而verification不需要。73 谓词逻辑公理{P1}S{P2}表示如果P1为真，则在S执行并终止后，P2将为真。如果A为真，则B也为真。逻辑公理：组合顺序1顺序2{P}S1{Q},{Q}S2{R}[组合语句]{P}S1;S2{R}{P}S{R},RQ[增加后置条件]{P}S{Q}PR,{R}S{Q}[增加前置条件]{P}S{Q}74 语句类型的公理条件语句1条件语句2While循环语句赋值语句{P^B}S{Q},P^not(B)Q{P}ifBthenS{Q}{P^B}S1{Q},{P^not(B)}S2{Q}{P}ifBthenS1elseS2{Q}{P^B}S{P}{P}whileBdoS{P^not(B)}，其中P为不变式{P(e)}x:=e{P(x)}，P(x)为x的谓词。75 公理化的程序证明给定程序：s1;s2;s3;s4;…sn及其规约：P和QP为前置条件Q为后置条件通过证明下列的谓词来证明{P}s1;…sn{Q}：{P}s1{p1}{p1}s2{p2}…{pn-1}sn{Q}反复运用组合公理，产生：{P}s1;…;sn{Q}76 例子{B>=0}1X:=B2Y:=03whileX>0do4begin5Y:=Y+A6X:=X-17end{Y=AB}即，给定非负的B，证明当程序终止时，Y=A*B.77 证明过程概要一般通过回溯来进行。首先，找到循环的不变式：Y为乘积的一部分，X为剩下的乘数因此，Y和X*A必须是所需的乘机，即不变式Y+X*A=A*B就是建议的不变式可以试着用(Y+X*A=A*BandX>=0)作为不变式78 证明赋值语句公理(6):{(Y+(X-1)A=A*BandX-1>=0)}X:=X-1{(Y+X*A=A*BandX>=0)}赋值语句公理(5):{((Y+A)+(X-1)A=A*BandX-1>=0)}Y:=Y+A{(Y+(X-1)*A=A*BandX-1>=0)}组合公理(5,6):{(Y+A)+(X-1)*A=A*BandX-1>=0)}Y:=Y+A;X:=X-1{(Y+X*A=A*BandX>=0)}数学定理:Y+X*A=A*BandX>0((Y+A)+(X-1)*A=A*BandX-1>=0)顺序语句公理:{Y+X*A=A*BandX>0}Y:=Y+A;X:=X-1{(Y+X*A=A*BandX>=0)}数学定理:(Y+X*A=A*BandX>=0)and(X>0)Y+X*A=A*BandX>0顺序语句公理:{(Y+X*A=A*BandX>=0)and(X>0)}Y:=Y+A;X:=X-1{(Y+X*A=A*BandX>=0)}[用**来代替]While循环语句公理:**{Y+X*A=A*BandX>=0}whileX>0doY:=Y+A;X:=X-1{(Y+X*A=A*BandX>=0)andnot(X>0)}79 证明(续)数学定理:(Y+X*A=A*BandX>=0)andnot(X>0)(Y+X*A=A*BandX=0)Y=AB顺序语句公理:{Y+X*A=A*BandX>=0}whileX>0doY:=Y+A;X:=X-1{Y+A*B}赋值语句公理:{0+X*A=A*BandX>=0}Y:=0{Y+X*A=A*BandX>=0}赋值语句公理:{0+B*A=A*BandB>=0}X:=B{0+X*A=A*BandX>=0)}组合公理:{0+B*A=A*BandB>=0}X:=B;Y:=0{Y+X*A=A*BandX>=0)}数学定理:(B>=0)0+B*A=A*BandB>=0顺序语句公理:{B>=0}X:=B;Y:=0{Y+X*A=A*BandX>=0)}组合公理:{B>=0}program{Y=A*B}80 公理化验证—小结需要为语言的所有特征建立公理，能否也为简单数组、过程调用、参数等建立公理？即使是要证明小程序也很困难，要证明大型程序就更困难了。还不能很好地处理非数学方面的问题，处理起来极端困难。很难自动化，而手工又会导致大量错误。但是准确，能够清楚地区别“程序是什么”以及“程序是如何解决问题”它是大多数其他验证方法的基础，包括半形式化的规范表示法。对于关键应用，付出的代价还是值得的。81 程序验证只有程序正确性的验证过程能够自动化，程序验证才有实际意义但要证明那些没有结构化的程序、以及那些具有复杂结构的程序的正确性，非常困难，基本上是不可能的。程序验证工作的研究成果通常用来指导程序设计语言的设计例如，在C++中加断言等。82 ML概述ML(元语言)是一种函数式语言，其程序的形式与C或Pascal相似。ML由RobinMilner于1970年代中期开发，是一种机器辅助形式化证明的机制。ML也可以作为一种通用符号操纵语言。1983，该语言中加入了模块等概念，并经过重新设计，形成了现在的标准ML。ML是一种具有静态类型、强类型、和函数式执行的语言，但类型不必由程序员来指定。ML程序由若干个函数定义构成。每个函数的类型是静态的，函数可以返回任意类型的值。因为是函数型的语言，变量的存储与C或Fortran语言的很不相同。ML可以通过其类型系统支持多态，还支持数据抽象。83 ML程序例子1fundigit(c:string):int=ord(c)-ord("0");2(*Storevaluesasalistofcharacters*)3funSumNext(V)=ifV=[]then(print("nSum=");0)4else(print(hd(V));5SumNext(tl(V))+digit(hd(V)));6funSumValues(x:string):int=SumNext(explode(x));7funProcessData()=8(letvalinfile=open_in("data.sml");9valcount=digit(input(infile,1))10in11print(SumValues(input(infile,count)))12end;13print("n"));84 把一个列表颠倒过来的函数datatypelist[a,b,c,d,e]hd(x)：列表的头，或第一个元素tl(x)：列表的尾，或除第一个元素外的元素x::y表示头为x，尾为y的列表x@y表示连接列表x和yfunreverse(L)=ifL=nilthennilelsereverse(tl(L))@[hd(L)];目标：将颠倒列表变成一个更简单的函数：列表要么是空的，否则，对表头和表尾进行处理将表尾颠倒，然后把表头连到后头。85 ML模式匹配上面的函数也可以写成：funreverse(x::y)=reverse(y)@[x]|reverse([])=[];在这个格式中，模式匹配就是寻找可以运用的函数定义：如果列表不为空，则匹配x::y；否则，匹配[]。86 ML的类型列表Lists:[a,b,c,d,e]所有的元素具有相同的类型元组Tuples:(“a”,1,2.3)简化的静态记录记录Records:{1=“a”,2=1,3=2.3}给出了选择子的名字构造动态的任意结构：datatypemoney=penny|nickel|dime;valx=penny;为常量设定值零钱的记录：datatypechange=coinsofmoney*int;coins(penny,3)类型为change的对象构造函数处理零钱：funNumPennies(coins(penny,x))=x;valx=coins(penny,5);NumPennies(x);valit=5:int;87 ML的结构硬币袋（Bagsofcoins）:datatypecoinbag=bagofcoinbag*coinbag|itemofchange|empty;funValuechange(coins(penny,X))=X|Valuechange(coins(nickel,X))=5*X|Valuechange(coins(dime,X))=10*X;funCountchange(bag(X,Y))=Countchange(X)+Countchange(Y)|Countchange(item(X))=Valuechange(X)|Countchange(Empty)=0;函数的使用：valx=bag(item(coins(dime,3)),item(coins(nickel,7)));Countchange(x);valit=65:int88'