最新相似三角形复习精选课件PPT课件.ppt 40页

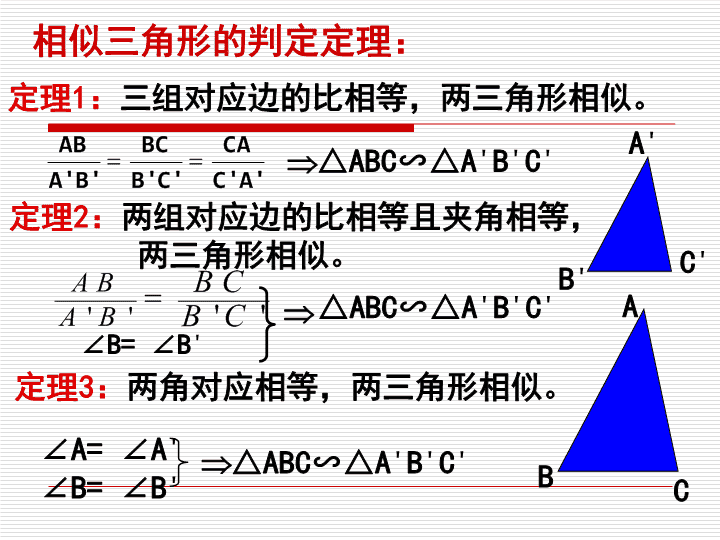
'相似三角形复习精选课件 三角形相似的判定方法有哪些？方法1：通过定义方法5：两组角分别对应相等，两个三角形相似方法2：平行于三角形一边的直线与其它两边相交，所得三角形与原三角形相似方法3：三组对应边的比相等，两个三角形相似方法4：两组对应边比相等且夹角相等，两个三角形相似 定理3：两角对应相等，两三角形相似。定理1：三组对应边的比相等，两三角形相似。∠A=∠A"∠B=∠B"△ABC∽△A"B"C"△ABC∽△A"B"C"定理2：两组对应边的比相等且夹角相等，两三角形相似。△ABC∽△A"B"C"∠B=∠B"A"C"B"ABC相似三角形的判定定理： 如图，∠ACB＝∠ADC＝90°，AC＝，AD＝2。问当AB的长为多少时，这两个直角三角形相似？DCBA∟∟ 要使这两个直角三角形相似，有两种情况：（1）当Rt△ABC∽Rt△ACD时，有（2）当Rt△ACB∽Rt△CDA时，有故当AB的长为3或时，这两个直角三角形相似。DCBA∟∟ 如图:∠ABC=∠CDB=90°,AC=a,BC=b,当BD=时，△ABC与△CDB相似.变式练∟∟ADBC 如图：已知∠ABC＝∠CDB＝90°，AC＝a，BC=b，当BD与a、b之间满足怎样的关系式时，两三角形相似DABCab解:⑴∵∠1＝∠D＝90°∴当时，即当时，△ABC∽△CDB,∴⑵∵∠1＝∠D＝90°∴当时,即当时，△ABC∽△BDC，∴答：略.１ 基本图形应用（1） 已知：如图，△ABC中，P是AB边上的一点，连结CP．满足什么条件时△ACP∽△ABC?解:⑴∵∠A=∠A，∴当∠1=∠ACB（或∠2=∠B）时，△ACP∽△ABC⑵∵∠A=∠A，∴当AC:AP＝AB:AC时，△ACP∽△ABC答：当∠1=∠ACB或∠2=∠B或AC:AP＝AB:AC时,△ACP∽△ABC.ABPC124 ABCDEE思维要严密ABCD如图△ABC中，AB=9，AC=6，D是边AB上一点且AD=2，E是AC上的点，则AE=时，△ADE与△ABC相似？或3△ADE∽△ABC? ABCDABCD练习EE已知，△ABC中，D为AB上一点，画一条过点D的直线(不与AB重合),交AC于E，使所得三角形与原三角形相似，这样的直线最多能画出多少条? 在△ABC中，AB>AC，过AB上一点D作直线DE（不与AB重合），交另一边于E，使所得三角形与原三角形相似，这样的直线最多能画出多少条?画出满足条件的图形.EDABCDABCDABCDABCEEE 在直角坐标系中，点A（－2，0），B（0，4），C（0，3）。过点Ｃ作直线交x轴于点Ｄ，使以Ｄ、Ｏ、Ｃ为顶点的三角形与ΔAOB相似，这样的直线最多可以作（）条A.2B.3C.4D.6ABCDDODD 动点与相似三角形 在平面直角坐标系中，四边形OABC为等腰梯形，OA∥BC,OA=7,BC=3,∠COA=60°,点P为线段OA上的一个动点，点P不与O、A重合，连结CP.（1）求点B的坐标。（2）点D为AB上一点，且AD:BD=3:5,连结PD,在OA上是否存在这样的点P,使∠CPD=∠BAO?若存在，求出直线PB的解析式，若不存在，请说明理由。OxyABCPD 如图：在⊿ABC中，∠C=90°,BC=8,AC=6.点P从点B出发，沿着BC向点C以2cm/秒的速度移动;点Q从点C出发，沿着CA向点A以1cm/秒的速度移动。如果P、Q分别从B、C同时出发，问：①经过多少秒时⊿CPQ∽⊿CBA;AQPCBAQPCB②经过多少秒时以C、P、Q为顶点的三角形恰好与⊿ABC相似？ 在平面直角坐标系内，已知点A（0，6）、点B（8，0），动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动，同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒．yxOPQAB(1)求直线AB的解析式；(2)当t为何值时，△APQ与△AOB相似？ 基本图形应用（2） 将两块完全相同的等腰直角三角板摆成如图的样子，假设图形中的所有点、线都在同一平面内，则图中有相似（不包括全等）三角形吗？如有，把它们一一写出来.解：有相似三角形，它们是：△ADE∽△BAE,△BAE∽△CDA，△ADE∽△CDA（△ADE∽△BAE∽△CDA）什么方法？EDBCGAF 已知：如图，△PQR是等边三角形，∠APB=120°求证：（1）PAQ∽△BPR．（2）PRQBA 如图点C、D在线段AB上，△PCD是等边三角形．（2）当△ACP∽△PDB时，求∠APB的度数（1）当AC、CD、DB满足怎样的关系式时，△ACP∽△PDBPDCBA F^※如图，已知EMAM，交AC于D，CE=DE求证：2ED·DM=AD·CD。∽分析：CMEDA∟ ∽如图，已知EMAM，交AC于D，CE=DE求证：2ED·DM=AD·CD。^GACEDM∟∟分析： 综合运用 已知如图，在△ABC中，AD是∠BAC的平分线，EF⊥AD于点F，AF＝FD。求证：DE²＝BE·CEABCDFE ※如图，已知点P是边长为4的正方形ABCD内一点，且PB=3BF⊥BP，垂足为B，请在射线BF上找一点M，使以点B、M、C为顶点的三角形与△ABP相似．FPDCBA则BM= ※正方形ABCD边长为4，M、N分别是BC、CD上的两个动点，当M点在BC上运动时，保持AM和MN垂直.（1）证明：Rt△ABM∽Rt△MCN；（2）当M点运动到什么位置时Rt△ABM∽Rt△AMN，求此时x的值.NMDCBA 提示(2)已知了这两个三角形中相等的对应角是∠ABM和∠AMN,如果要想使RT△ABM∽RT△AMN，那么两组直角边就应该对应成比例，即AM/MN=AB/BM，根据（1）的相似三角形可得出AM/MN=AB/MC,因此BM=MC，M是BC的中点，即X=2 再见 狐狸和乌鸦九义教材小学语文第三册 5123451234 狐狸想了想，就笑着对乌鸦说：“您好，亲爱的乌鸦！”乌鸦不做声。全 狐狸又说：“亲爱的乌鸦，您的孩子好吗？”乌鸦看了狐狸一眼，还是不做声.。全 狐狸又说：“亲爱的乌鸦，您的羽毛真漂亮，麻雀比起你来，可就差多了。你的嗓子真好，谁都爱听您唱歌。您唱几句吧！”全 乌鸦听了狐狸的话得意极了，就唱起歌来。哇……他刚一张嘴，肉就掉下来了。全 狐狸想了想，就笑着对乌鸦说：“您好，亲爱的乌鸦！”乌鸦不做声。狐狸又说：“亲爱的乌鸦，您的孩子好吗？”乌鸦看了狐狸一眼，还是不做声。狐狸又说：“亲爱的乌鸦，您的羽毛真漂亮，麻雀比起你来，可就差多了。你的嗓子真好，谁都爱听您唱歌。您唱几句吧！”乌鸦听了狐狸的话得意极了，就唱起歌来。哇……他刚一张嘴，肉就掉下来了。'