[整理]咬文嚼字课件PPT.ppt 53页

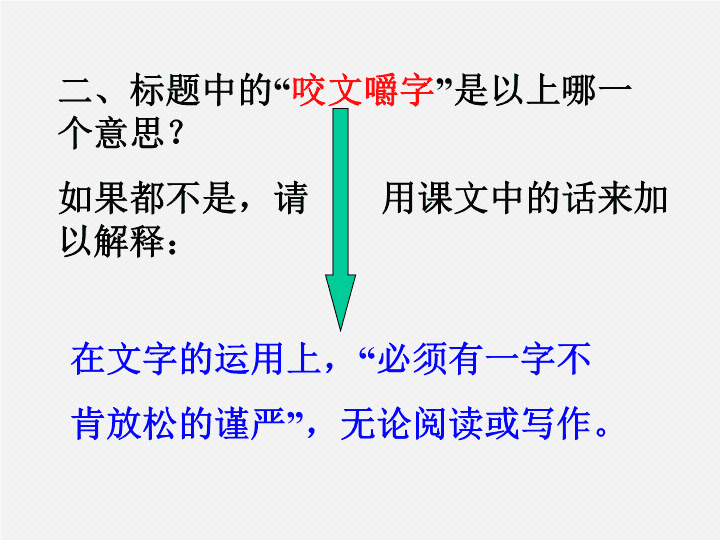
'咬文嚼字 一、“咬文嚼字”有以下几个意思，请选择每句中的“咬文嚼字”的正确意思：A.过分地斟酌字句(多指死抠字眼而不领会精神实质)。B.形容卖弄才学。C.形容强词夺理或狡辩。1、学习马列主义理论要领会其精神实质,切不可一味地咬文嚼字。（　　　）2、此君肚里学识稀薄,但在人前说起话来却常常咬文嚼字,极尽哗众取宠之能事。（　　　）3、此事明明是你错了,你再咬文嚼字也毫无用处。（）ABC 二、标题中的“咬文嚼字”是以上哪一个意思？如果都不是，请用课文中的话来加以解释：在文字的运用上，“必须有一字不肯放松的谨严”，无论阅读或写作。 本文的中心论点是：Ａ　必须“惟陈言之务去”Ｂ　推敲文字是为了语句通晓漂亮Ｃ　文学是艰苦的事Ｄ　无论阅读或写作，都必须有一字不肯放松的谨严如何理解“咬文嚼字，在表面上像只是斟酌文字的分量，在实际上就是调整思想和情感”这种观点？文学借文字表现思想情感；文字上面有含糊，就显得思想还没有透彻，情感还没有凝练。————朱光潜对下面文字进行对比，体会其思想感情的不同：A“敢于这样做的人，肯定是个英雄。”Ｂ　“敢于这样做的人，难道不是一个英雄吗？可以肯定说是一个英雄，一个大大的英雄。”————《内蒙访古》D 题李凝幽居贾岛闲居少邻并，草径入荒园。鸟宿池边树，僧敲月下门。过桥分野色，移石动云根。暂去还来此，幽期不负言。一条杂草遮掩的小路通向荒芜的小园；近旁，亦无人家居住。一阵轻微的敲门声，惊动了树上的宿鸟，过桥时色彩斑斓的原野；晚风轻拂，云脚飘移，仿佛山石在移动。我暂时离去，不久定当重来，不负共同归隐的约期。 三、完成课后练习一，每个例子说明的道理用不超过10个字的话来概括。1、“你是没有骨气的文人”一句的修改和《史记》李广射虎一段的改写，说明2、“僧敲月下门”一句的推敲，说明3、《惠山烹小龙团》三、四两句的剖析，说明4、“柳面桃腰”等套语的评述，说明说法不同，意味不同字眼不同，意境不同善用联想义，意蕴丰富套板反应，易生流弊 四、请根据特定的情景增加词语，使下面的文字表现出特定的内容。早晨，太阳发出光芒，树上的鸟儿鸣叫着，树下的流水流向远方。示例１、要求扩展后的句子要抒发主人公欢快的心情。早晨，温暖的太阳发出金色的光芒，树上有几只可爱的鸟儿清脆地鸣叫着，树下清澈的流水欢快地流向远方。 2、要求扩展后的句子要抒发主人公苦闷伤感的心情。示例早晨，太阳发出凄清而冷寂的光芒，光秃秃的树上几只寂寞的鸟儿凄惶地鸣叫着，树下的流水在清冷的寒风中无言地流向远方。 句式不同意味不同字数不同意味不同字眼不同意境不同思想感情善用字的联想意义套板效应 两句三年得,一吟双泪流。——唐·贾岛吟安一个字,拈断数茎须。——唐·卢延让古人不废炼字法,然以意胜,而不以字胜,故能平字见奇,常字见险,陈字见新,朴字见色。——清·沈德潜 无论你所要讲的是什么,真正能够表现它的句子只有一个,真正适用的动词和形容词也只有一个,就是那最准确的一句、最准确的一个动词和形容词。其他类似的却很多。而你必须把这唯一的句子、唯一的动词、唯一的形容词找出来。——福楼拜对莫泊桑如是说 咬文嚼字示例眼看朋辈成新鬼,怒向刀边觅小诗。——鲁迅<<惯于长夜过春时>>(忍)(丛) (林冲)便去包裹里取些碎银子,把花枪挑了酒葫芦,将火炭盖了,取毡笠子戴上,拿了钥匙,出来,把草厅门拽上;出到大门首,把两扇草场门反拽上锁了;带了钥匙,信步投东,雪地里踏着碎琼乱玉,迤逦背着北风而行。那雪正下得()。(A大B快C紧D密)——施耐庵<<水浒>>第10回紧 第三章工业机器人运动学 引言要实现对工业机器人在空间运动轨迹的控制，完成预定的作业任务，就必须知道机器人在空间瞬时的位置与姿态。如何计算机器人手部在空间的位姿是实现对机器人的控制首先要解决的问题。本章讨论机器人运动学的基本问题，将引入齐次坐标变换。推导出坐标变换方程；利用DH参数法，进行机器人的位姿分析；介绍机器人正向和逆运动学的基础知识。 主要内容数学基础——齐次坐标变换机器人运动学方程的建立（正运动学）机器人逆运动学分析 一、机器人数学基础——齐次坐标变换1.1引言1.2点向量和平面的描述1.3变换1.4平移变换1.5旋转变换1.6坐标系1.7相对变换1.8物体的描述1.9逆变换1.10一般性旋转变换1.11等价旋转角与旋转轴1.12扩展与缩小1.13透视变换1.14变换方程1.15小结 1.1引言(Introduction)机器人操作涉及到各物体之间的关系和各物体与机械手之间的关系。这一章将给出描述这些关系必须的表达方法。类似这种表示方法在计算机图形学中已经解决。在计算机图形学和计算机视觉中，物体之间的关系是用齐次坐标变换来描述的。在本课程我们将采用齐次坐标变换来描述机械手各关节坐标之间、各物体之间以及各物体与机械手之间的关系。本章首先介绍向量和平面的表示方法，然后引出向量和平面的坐标变换，这些变换基本上是由平移和旋转组成，因此可以用坐标系来描述各种物体和机械手的空间位置和姿态。稍后还要介绍逆变换，逆变换是运动学求解的基础。 a0vzyxzyxpcb0uEH图1.1点向量的描述•1.2点向量和平面的描述（Notationofpointvectorsandplanes）1.2.1点向量（Pointvectors）点向量描述空间的一个点在某个坐标系的空间位置。同一个点在不同坐标系的描述及位置向量的值也不同。如图1.1中，点p在E坐标系上表示为Ev，在H坐标系上表示为Hu，且v≠u。一个点向量可表示为v=ai+bj+ck通常用一个（n+1）维列矩阵表示，即除x、y、z三个方向上的分量外，再加一个比例因子w，即v=[xyzw]T其中a=x/w,b=y/w,c=z/w。改变比例因子w，则分量a、b、c的数值相应改变，但描述的还是同一个点向量。如v=3i+4j+5k可表示为v=[3451]T=[68102]T=[-3-4-5-1]T在向量中增加一个比例因子w是为了方便坐标变换中的矩阵运算。 已知两个向量a=axi+ayj+azkb=bxi+byj+bzk（1.1）向量的点积是标量。用“·”来定义向量点积，即a·b=axbx+ayby+azbz（1.2）向量的叉积是一个垂直于由叉积的两个向量构成的平面的向量。用“×”表示叉积，即a×b=(aybz¯azby)i+(azbx¯axbz)j+(axby¯ayby)k（1.3）可用行列式表示为ijka×b=axayaz（1.4）bxbybz 1.2.2平面（Planes）平面可用一个行矩阵表示，即p=[abcd]（1.5）它表示了平面p的法线方向，且距坐标原点的距离为－d/m，其中m=（1.6）如图1.2所示，如果将x－y平面沿z轴正方向平移一个单位距离，构成平面p，则p=[001-1]即a=0,b=0,c=1,d=-1,m==1平面p上任一点v为v=[xy11]T，它与平面p的点乘为零，即p•v=0平面p上方任一点v，如v=[0021]T，它与平面p的点乘为一个正数，即p•v=1平面p下方任一点v，如v=[0001]T，它与平面p的点乘为一个负数，即p•v=-1注意：平面[0000]无定义。a2+b2+c2a2+b2+c2图1.2平面的描述0•vpzyx1yx H空间的变换是由4×4矩阵来完成的，它可以表示平移、旋转、扩展和透视等各种变换。如已知点u（在平面p上）,它的变换v（在平面q上）用矩阵积表示为v=Hu（1.7）其中H为4×4变换矩阵，u和v为4×1的点列向量，相应的平面p到q的变换是q=pH-1（1.8）其中H-1为H的逆阵，p和q为1×4的平面行向量。经变换后的平面向量q与点向量v的点乘为q·v=pH-1·Hu＝p·u（1.9）与变换前平面p与点u的点乘相等，证明了变换的等效性。1.3变换(Transformation) 1.4平移变换（Translationtransformation）用向量h＝ai+bj+ck进行平移，其相应的H变换矩阵是100a010bH=Trans(abc)=001c(1.10)0001因此对向量u=[xyzw]T，经H变换为向量v可表示为x+awx/w+ay+bwy/w+bv=z+cw=z/w+c(1.11)w1可见，平移实际上是对已知向量u=[xyzw]T与平移向量h=[abc1]T相加。 【例1.1】对点向量u=[2321]T进行平移，平移向量为h=[4-371]T，则平移后的向量为v=[6091]T，或100426010―330v=H∙u=00172=9000111点向量的平移过程如图1.3所示。对平面的平移则用H－1进行变换，如对平面p=[100-2]进行H变换为平面q，则根据变换原理有100-40103q＝pH－1＝[100-2]001-70001＝[100-6]平面p＝[100-2]是y－z平面沿x正方向移动2个单位形成的平面（图1.3），点u=[2321]T是平面p上的一个点，它们的点乘p∙u=0。经H变换后的平面q＝[100-6]是y－z平面沿x正方向移动6个单位形成的平面，点v=[6091]T是平面q上一个点，平面q与点v的点乘也应是零，即q∙v＝0，说明变换前后的结果不变，证明H变换是正确的。u•0zyx3P22图1.3点向量的平移•v69qp 1.5旋转变换（Rotationtransformation）如图1.4所示，绕x,y,z轴旋转一个θ角的相应变换是10000cosθ-sinθ0Rot(x,θ)=0sinθcosθ0（1.12）0001cosθ0sinθ00100Rot(y,θ)=-sinθ0cosθ0(1.13)0001cosθ-sinθ00sinθcosθ00Rot(z,θ)=0010(1.14)0001注意：θ角旋转的正方向遵循右手螺旋法则（如图1.4所示）图1.4旋转变换θ0zyxθθ 【例1.2】点u=7i+3j+2k，它绕z轴旋转90°为v，经式（1.14）变换得到（sinθ=1，cosθ=0）0-1007-3100037v=Rot(z,90°)=00102＝2000111起始点u和终点v如图1.5所示。如将v点再绕y轴旋转90°得到w。用式（1.13）变换得到0010-32010077w=Rot(y,90°)=-10002＝3000111结果如图1.6所示。如果将上述两次旋转结合起来，写成一个表达式得到w=Rot(y,90°)v＝Rot(y,90°)Rot(z,90°)u用两个变换矩阵Rot(y,90°)、Rot(z,90°)和起始点u代入上式计算的结果与前面分两次计算的结果相同。2•uzyx•v0图1.5Rot(z,90°)yuv0zx•w••图1.6Rot(y,90°)Rot(z,90°)27 为此，先将点u绕z轴旋转90°，然后再绕y轴旋转90°，我们得到00100-100720100100037w＝Rot(y,90°)Rot(z,90°)u=-100000102＝30001000111如果按着逆序旋转，首先绕y轴旋转90°，然后再绕z轴旋转90°，其结果为0-10000107-31000010032w=Rot(z,90°)Rot(y,90°)u=0100-10002=-70001000111逆序旋转的结果如图1.7所示。显然，变换的顺序不同，其结果也不同。这从矩阵相乘是不可交换的（AB≠BA）也可以得到证明。 如对经过两次旋转变换得到的点向量w再进行一次平移（平移向量为h＝[4-371]T），则可得到如图1.8所示的点向量n。变换过程如下100426010-374n=Trans(4,－3,7)w=00173=10000111zuv0yx•w••图1.8Trans(4,-3,7)Rot(y,90°)Rot(z,90°)•••n72w0zyx•••u图1.7Rot(z,90°)Rot(y,90°)2-7v 1.6坐标系(Coordinateframes)齐次变换矩阵H由四个列向量组成，它的前三个列向量称为方向向量，由式（1.12）到式（1.14）的旋转变换（分别绕x、y、z轴旋转θ角）确定，第四个列向量称为平移向量，它的平移分量（沿x、y、z轴的平移量）由式（1.10）第四列的前三个元素确定。如0014100-3H＝Trans(4,-3,7)Rot(y,90°)Rot(z,90°)=0107（1.15）0001坐标系的原点，即零向量[0001]T的H变换是[4-371]T，相当于将原点按平移向量的各个分量进行平移的结果（如图1.9所示）。如果对x、y、z轴的单位向量进行H变换，分别得到[4-271]T、[4-381]T和[5-371]T。这四个向量在图1.9中标出，并形成了一个新坐标系。0zyxzyx0Trans(4,-3,7)Rot(z,90°)Rot(y,90°)图1.9坐标原点与单位向量的H变换 这个新坐标系的x、y、z轴的方向分别是[0，1，0，0]T、[0，0，1，0]T和[1，0，0，0]T，它是由单位向量的H变换减去这个坐标原点的向量得到的。这些方向向量相应于变换矩阵的前三列（见式（1.15））。可见，H变换矩阵描述了一个坐标系绕原参考坐标系旋转和对参考坐标系平移的三个轴的方向和原点的位置（见图1.9）。如图1.10所示，当对一个向量n进行式（1.15）给出的H变换时，原向量n可以被认为是在新坐标系描述的那个向量u，即被变换了的向量u就是相对于参考坐标系描述的同一个向量n。00zzyyxxu(7,3,2,1)•n(6,4,10,1)图1.10向量的H变换 1.7相对变换（Relativetransformation）我们刚刚描述的旋转和平移都是相对于一个固定的坐标系而进行的。这样，在已给的例子里0014100-3Trans(4,-3,7)Rot(y,90°)Rot(z,90°)=0107（1.16）0001坐标系首先绕参考坐标系z轴旋转90°，然后绕y轴旋转90°，最后平移4i－3j+7k，如图2.9所示。如果以相反次序从左到右来进行这些操作：首先对坐标平移4i―3j+7k，然后将它绕当前坐标系的y轴旋转90°，此时当前坐标系的y轴与参考坐标系的y轴是相同的。然后再绕着新坐标系（当前的）坐标系的z轴旋转90°，所得结果与前面的方法相同（见图1.11）。 •00zzzzyyyyxxxxRot(y,90°)Rot(z,90°)Trans(4,-3,7)坐标原点图1.11相对变换 一般的情况下，如果我们用一个旋转和/或平移变换矩阵右乘一个坐标系的变换，那么产生的平移和/或旋转是相对于前一个变换的坐标系（当前坐标系）的轴来说的。如果我们用一个描述平移和/或旋转的变换矩阵左乘一个坐标系的变换，那么产生的平移和/或旋转是相对于基坐标系来说的。【例1.3】给一个坐标系C和一个变换T，T为绕z轴旋转90°，并在x轴方向上平移10个单位，当变换是相对于基坐标系产生时，我们用T左乘C得到新的位置x为0-1010100200010100000-11010020x=TC=00100100＝0100（1.17）000100010001当变换是相对于当前坐标系C轴产生时，我们用T右乘C得到新的位置y为100200-10100-103000-110100000-110y=CT=01000010＝1000（1.18）000100010001结果如图1.12所示。 YXTrans(10,0,0)Rot(z,90°)0zyxxxxxyyyyzzzzRot(z,90°)Trans(10,0,0)图1.12相对于基坐标系和当前坐标系的变换 1.8物体的描述（Objectrepresentation）变换可用来描述物体的位置与方向（方位）。如图1.13所示的楔形物体用六个角点来描述，这六个角点是相对于物体所在的参考坐标系的。如果把物体绕z轴旋转90°，然后绕y轴旋转90°，接着沿x方向平移4个单位，我们可以描述这个变换为00141000Trans(4,0,0)Rot(y,90°)Rot(z,90°)=01000001这个变换表示了对参考坐标系的旋转和平移操作，变换后物体的六个角点为44664400141-1-111-11-1-111-11000000044000044=01000002201111110001111111变换后该物体在坐标上的方位如图1.13所示。 从图1.13可以看出，由于楔形物体的角点与它所在的坐标系有固定的关系，因此没有必要对所有的角点进行变换，只要对物体所在的坐标系进行变换，就可得到变换后的各个角点在基坐标中的位置，将这些角点用直线连接起来就可得到楔形物体的边缘，它与逐点变换的结果完全相同（见图1.14）。(-1,0,0)(-1,0,2)(1,0,2)(1,4,0)(-1,4,0)(1,0,0)zyx0图1.13楔形物体图1.14被变换的楔形物体(4,1,0)(4,-1,4)(4,1,4)(6,1,0)(6,-1,0)(4,-1,0)yx0yxzz 1.9逆变换（Inversetransformation)所谓逆变换就是将被变换的坐标系返回到原来的坐标系，在数学上就是求变换矩阵的逆。下面我们写出变换矩阵的一般表达形式nxoxaxpxnyoyaypyT=nzozazpz（1.19）0001式中n,o,a是旋转变换列向量，p是平移向量，其逆是nxnynz-p.noxoyoz-p.oT-1=axayaz-p.a（1.20）0001式中的“.”表示向量的点积。这个结果很容易用式1.19右乘式1.20是单位矩阵来证明。 1.10一般性旋转变换（Generalrotationtransformation）前面我们介绍的旋转变换都是绕x，y，z轴旋转的旋转变换，这些变换都有一个简单的几何解释。例如：在绕z轴旋转的情况下，表示z轴保持恒定，x轴和y轴将如图1.15所示那样变化。图1.15绕z轴的旋转θz0zyyxxCosθ－SinθSinθCosθθ 如图1.16所示，给出一个变换矩阵C，它绕任意向量k旋转，我们把k当作C坐标系的z轴单位向量。nxoxax0nyoyay0C=nzozaz0（1.21）0001k=axi+ayj+azk（1.22）绕k旋转就相等于绕C坐标系的z轴旋转。Rot（k，θ）=Rot（Cz，θ）（1.23）如果我们给一个坐标系T，它在参考坐标系里被描述，它在C坐标系里用X描述，这样T=CX（1.24）其中X描述T相对C的位姿，求X，我们得到X=C-1T（1.25）kTzzyyxxx00图1.16一般性旋转变换C T绕k旋转就等于Ｘ绕Ｃ坐标系的z轴旋转Rot（k,θ）Ｔ＝CRot（z,θ）X（1.26）Rot（k,θ）Ｔ＝CRot（z,θ）C-1T（1.27）这样Rot（k,θ）＝CRot（z,θ）C-1（1.28）展开式（1.28），我们发现CRot（z,θ）C-1仅是k的函数。用C-1右乘Rot（z,θ），我们得到cosθ-sinθ0　0　　nxnynz0sinθcosθ00　　oxoyoz0Rot（z,θ）C-1＝　00　10　　axayaz00　　0　010001nxcosθ－oxsinθnycosθ―oysinθnzcosθ―ozsinθ0nxcosθ+oxsinθnycosθ+oysinθnzcosθ+ozsinθ0=axayaz0（1.29）0001再用C左乘nxoxax0nyoyay0C=nzozaz0（1.30）0001 得到CRot（z,θ）C-1=nxnxcosθ―nxoxsinθ+nxoxsinθ+oxoxcosθ+axaxnynxcosθ―nyoxsinθ+nxoysinθ+oyoxcosθ+ayaxnznxcosθ―nzoxsinθ+nxozsinθ+ozoxcosθ+azax0nxnycosθ―nxoysinθ+nyoxsinθ+oyoxcosθ+axaynynycosθ―nyoysinθ+nyoysinθ+oyoycosθ+ayaynznycosθ―nzoysinθ+nyozsinθ+oyozcosθ+azay0nxnzcosθ―nxozsinθ+nzoxsinθ+ozoxcosθ+axaz0nynzcosθ―nyozsinθ+nzoysinθ+ozoycosθ+ayaz0nznzcosθ―nzozsinθ+nzozsinθ+ozozcosθ+azaz0（1.31）01 应用下列关系进行简化：C坐标系任意的行或列与其他行或列的点积为零，因为这些向量是正交的；C坐标系任意的行或列与其自身的点积为I，因为它们是单位量；z向量是x和y向量的叉积：a=n×o，它有下列分量ax=nyoz―nzoyay=nzox―nxozaz=nxoy―nyox正矢Versθ=（1―cosθ），简写成Versθ，且kx=ax，ky=ay，kz=az。由此可得到简化式为Rot(k,θ)=kxkxVersθ+cosθkykxVersθ―kzsinθkzkxVersθ+kysinθ0kxkyVersθ+kzsinθkykyVersθ+cosθkzkyVersθ―kzxsinθ0kxkzVersθ―kysinθkykzVersθ+kxsinθkzkzVersθ+cosθ0（1.32）0                                   0                                  01上式是一般性的旋转变换的重要结论。从这个结论可以得出每一个基本旋转变换。例如：Rot(x,θ)就是Rot(k,θ)当kx=1，ky=0,kz=0的情况，将这些值代入式（1.32）得到10000cosθ-sinθ0Rot(x,θ)=0sinθcosθ0（1.33）0001这个结果与以前一样。 1.11等价旋转角与旋转轴（Equivalentangleandaxisofrotation）任给一个旋转变换，从（1.32）方程得到一个轴，绕这个轴旋转的等价旋转角可由如下方法得到。已知一个旋转变换Rnxoxax0nyoyay0R=nzozaz0（1.34）0001令R和式（1.32）的Rot(k,θ)相等，并将对角线各项相加得到nx+oy+az+1=k2xVersθ+cosθ+k2yVersθ+cosθ+k2zVersθ+cosθ+1（1.35）nx+oy+az=(k2x+k2y+k2z)Versθ+3cosθ=1+2cosθ（1.36）由此可得到旋转角的余弦是cosθ=1/2（nx+oy+az―1）（1.37）对非对角线项相减，我们得到oz―ay=2kxsinθ（1.38）ax―nz=2kysinθ（1.39）ny―ox=2kzsinθ（1.40）把式（1.38）到式（1.40）两边平方并相加有（oz―ay）2+（ax―nz）2+（ny―ox）2=4sin2θ（1.41） 我们得到了sinθ的表达式sinθ=±1/2√（oz―ay）2+（ax―nz）2+（ny―ox）2（1.42）规定这个旋转是绕k正方向旋转，当0≤θ≤180°时，在上式中取十号是合理的。这个旋转角θ被唯一定义为tanθ=√（oz―ay）2+（ax―nz）2+（ny―ox）2/（nx+oy+az―1）（1.43）k的各分量为kx=（oz―ay）/2sinθ（1.44）ky=（ax―nz）/2sinθ（1.45）kz=（ny―ox）/2sinθ（1.46）注意：当旋转角θ较小或接近180°时，上述三个式子的分子和分母都很小，所计算的k值是不精确的。为此可继续根据式（1.32）和式（1.33）对应元素以及它们的代数和相等的关系来求出k的各个分量。 1.12扩展与缩小（Stretchingandscaling）一个变换Ta0000b00T=00c0（1.47）0001将沿着x轴以a因子，沿着y轴以b因子，沿着z轴c因子均匀扩展着各种物体。假定在一个物体上任意一个点xi+yj+zk，它的变换是axa000xby0b00ycz=00c0z（1.48）100011这个正好表示出所说的扩展。这样，一个正方体可以由这个变换变成长方体。变换ss0000s00s=00s0（1.49）0001将以s为比例因子来扩展或缩小任一物体。 1.13透视变换（Perspectivetransformation）假设由一个简单透镜把一个物体形成的像如图1.17所示。透镜的轴沿着y的方向，焦距为f，物体上的一个点x,y,z成象为x/,y/,z/。y/表示象距，它随着物距y而变化。如果在通过y/而垂直于y的平面（照相机的底片）上画出各个点，那么就形成了一个透视像。射线穿过透镜中心不偏转，则z/y=z//y/（1.50）x/y=x//y/（1.51）根据平行透镜的轴的射线通过焦点，我们可以写出z/f=z//(y/+f)（1.52）x/f=x//(y/+f)（1.53）x/y/和z/是负数，而f是正数。用式（1.50）和式（1.52）消去y/，得z/f=z/(z/y/z+f)（1.54）zyx0(x’,y’,z’)(x,y,z)••f•图1.17透视变换 求出x/=x(1―y/f)（1.55）y/=y(1―y/f)（1.56）z/=z(1―y/f)（1.57）齐次变换p能导出同样结果，变换p是10000100p=0010（1.58）0-1/f01任何一点xi+yj+zk变换为x1000xy0100yz=0010z（1.59）1―y/f0-1/f011用比例因子1―y/f除得到的象点x/,y/,z/有[x/(1―y/f)]i+[y/(1―y/f)]j+[z/(1―y/f)]k（1.60）这个结果与前面利用透视原理的结果完全相同。在p变换的第二列最底一元素为―1/f，则导出一个沿着y轴的一透视变换。如果―1/f是第三列最底一项，那就是沿z轴的透视变换。 1.14变换方程（Transformequations）研究一下图1.18描述的一个物体与机械手情况，机械手用变换Z相对于基坐标系被定位。机械手的端点用变换ZT6来描述，而末端执行器用变换T6E来描述。物体用变换B相对于基坐标系被定位。最后，机械手末端抓手用变换BG相对于物体被定位。末端抓手位置的描述有两种方式，一种是相对于物体的描述，一种是相对于机械手的描述。由于两种方式描述的是同一个点，我们可以把这个描述等同起来，得到ZZT6T6E=BBG（1.61）这个方程可以用有向变换图来表示（见图1.19）。图的每一段弧表示一个变换。从它的定义的坐标系向外指向。用Z-1左乘和用E-1右乘方程（1.61），得到T6=Z-1BGE-1（1.62）0EGBZT6zyx图1.18一个物体与机械手•图1.19有向变换图GBET6Z••0 从有向变换图上我们可以直接得到上述结果，从T6弧线的尾部开始，沿着图形顺时针依次列出各个变换，直到T6弧的箭头为止。在逆变换时，我们从T6弧的箭头开始，按逆时针方向依次列出各个变换，直到T6弧的起始点为止，则可得到T6的逆T6-1=EG-1B-1Z（1.63）对上式求逆得到与式（1.62）完全相同的结果。作为进一步的例子，假设一个物体B的位置不知道，但机械手移动，使得末端抓手正好定位在物体上面。然后用G-1右乘式（1.61）求出B。或者在有向变换图中从B的尾部沿着逆时针方向到达弧B的箭头，直接得到同样结果。B=ZT6EG-1（1.64）同样，我们可以用有向变换图求出变换的连接组。例如ZT6=BGE-1（1.65）用有向变换图简化了变换方程的求解，可以直接写出变换结果。为了避免画圆，我们用图1.20所示的形式表示这个变换图，其中虚线表示那两个节点是被连在一起的，中间各垂线段表示相对坐标系。BGET6Z图1.20有向变换图的另一种形式 1.15小结（Summary）齐次变换可以用来描述空间坐标系的位置与方向。如果坐标系被固定在物体或机械手连杆上，那么该物体或机械手的位置与方向同样很容易被描述。物体A相对于物体B的齐次变换可以求其逆，来获得物体B相对于物体A的描述。变换可以表示为旋转变换和/或平移变换的乘积。如果变换是从左到右，那么旋转和/或平移是相对于当前的坐标系。如果变换是从右到左，那么旋转和/或平移是相对于参考坐标系进行。齐次变换用正交分量来描述坐标系，即用角度的正弦和余弦。这种描述可与旋转联系起来。在一般性旋转的情况下，旋转是绕任意向量旋转θ角。'