最新2.4.1-抛物线及其标准方程(2)课件PPT.ppt 35页

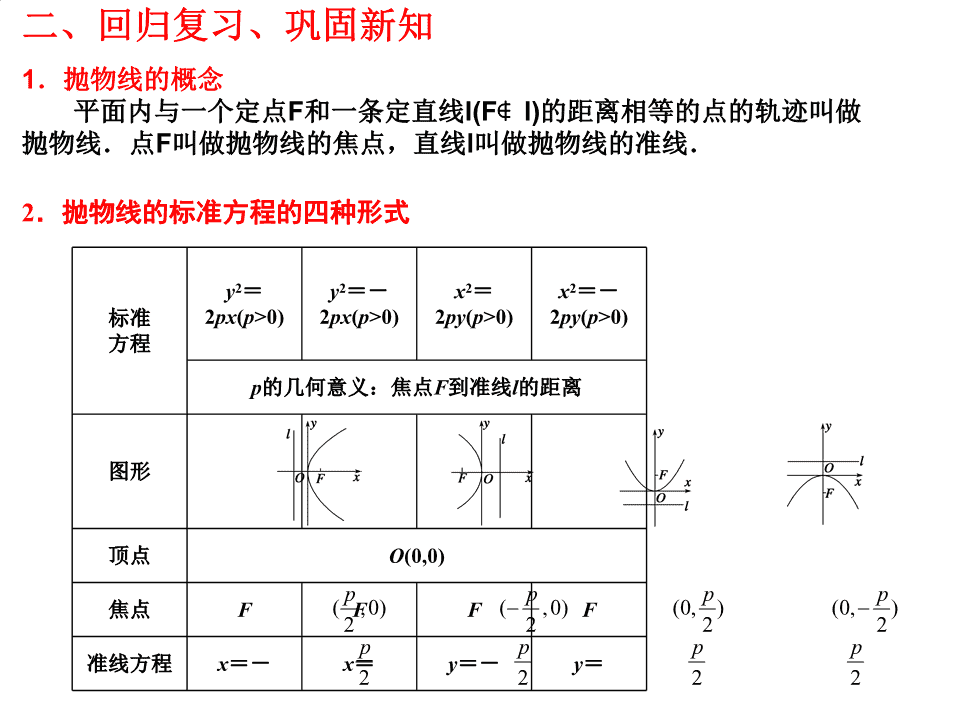
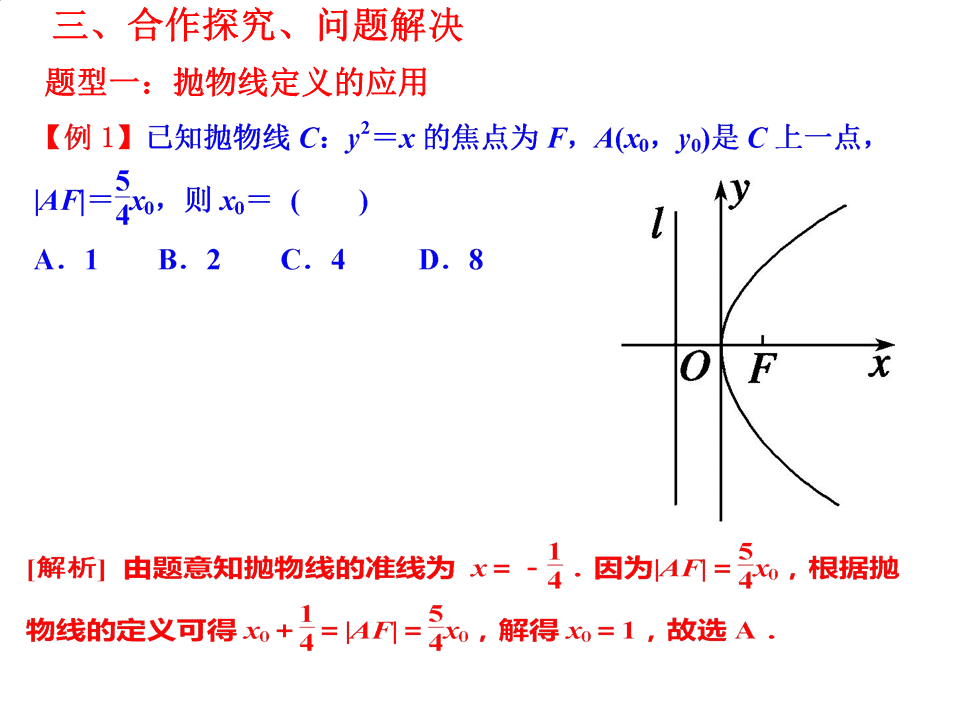
' 二、回归复习、巩固新知1．抛物线的概念平面内与一个定点F和一条定直线l(F∉l)的距离相等的点的轨迹叫做抛物线．点F叫做抛物线的焦点，直线l叫做抛物线的准线．2．抛物线的标准方程的四种形式y2＝y2＝－x2＝x2＝－标准2px(p>0)2px(p>0)2py(p>0)2py(p>0)方程p的几何意义：焦点F到准线l的距离图形顶点O(0,0)pppp焦点F(F,0)F(,0)F(0,)(0,)2222pppp准线方程x＝－x＝y＝－y＝2222 三、合作探究、问题解决题型一：抛物线定义的应用 三、合作探究、问题解决题型一：抛物线定义的应用 三、合作探究、问题解决题型二：利用抛物线的定义求最值【例2】已知点P是抛物线y2＝2x上的一个动点，求点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值． 三、合作探究、问题解决题型二：利用抛物线的定义求最值【例2】已知点P是抛物线y2＝2x上的一个动点，求点P到点A(0,2)的距离与P到该抛物线准线的距离之和的最小值． 三、合作探究、问题解决题型二：利用抛物线的定义求最值【变式训练3】已知抛物线y2＝2x的焦点是F，点P是抛物线上的动点，又有点A(3,2)，求|PA|＋|PF|的最小值，并求出取最小值时点P的坐标. 三、合作探究、问题解决题型二：利用抛物线的定义求最值 三、合作探究、问题解决题型三：利用抛物线的定义求轨迹【例3】点M与点F（4，0）的距离比它到直线l:x+5=0的距离小1，求点M的轨迹方程.解：如图所示，设点M的坐标为（x,y)由已知条件可知，点M与点F的距离等于它到直线x+4=0的距离.根据抛物线的定义，点M的轨迹是以F（4，0）为焦点的抛物线.p∵2=4，∴p=8,因为焦点在x轴的正半轴上，所以点M的轨迹方程为y2=16x. 三、合作探究、问题解决题型三：利用抛物线的定义求轨迹【变式训练4】点P与点F（0，2）的距离比它到直线y+4=0的距离小2，求点P的轨迹方程.解：设点P的坐标为（x,y)，由已知条件可知，点P与点F的距离等于它到直线y+2=0的距离.根据抛物线的定义，点M的轨迹是以F（0，2）为焦点的抛物线.p∵=2，∴p=4,2因为焦点在x轴的正半轴上，所以点P的轨迹方程为x2=8y. 四、课堂小结、教学反思1．抛物线的定义根据抛物线的定义，抛物线上任意一点到焦点的距离等于它到准线的距离，因此，由抛物线定义可以实现点点距离与点线距离的相互转化，从而简化某些问题．2．解决最值问题．在抛物线中求解与焦点有关的两点间距离和的最小值时，往往用抛物线的定义进行转化，即化折线为直线解决最值问题．3．解决轨迹问题．求有关抛物线的轨迹方程时，要依据题设条件，弄清抛物线的对称轴和开口方向，正确地选择抛物线的标准方程． 五、课后练习、作业回馈1．已知F是拋物线y2＝x的焦点，A，B是该拋物线上的两点，|AF|＋|BF|＝3，则线段AB的中点到y轴的距离为()357A．B．1C．D．4442．已知点P在抛物线y2＝4x上，那么点P到点Q(2，－1)的距离与点P到抛物线焦点距离之和取最小值时，点P的坐标为()11A.(,1)B.(,1)C．(1,2)D．(1，－2)443．若点P到直线y＝－1的距离比它到点(0，3)的距离小2，则点P的轨迹方程是__________. 三、合作探究、问题解决题型一：抛物线定义的应用 五、课后练习、作业回馈1．经过抛物线C的焦点F作直线l与抛物线C交于A、B两点，如果A，B在抛物线C的准线上的射影分别为A1，B1，那么∠A1FB1为()2A．B．C．D．64232．已知F是拋物线y2＝x的焦点，A，B是该拋物线上的两点，|AF|＋|BF|＝3，则线段AB的中点到y轴的距离为()357A．B．1C．D．4443．已知点P在抛物线y2＝4x上，那么点P到点Q(2，－1)的距离与点P到抛物线焦点距离之和取最小值时，点P的坐标为()11A.(,1)B.(,1)C．(1,2)D．(1，－2)444．若点P到直线y＝－1的距离比它到点(0，3)的距离小2，则点P的轨迹方程是__________. 第九章色散限制、补偿和管理9.1色散引起的脉冲展宽9.2色散对系统性能的限制9.3色散补偿技术9.4色散管理 •损耗：光纤放大器的实用化•色散：•色散补偿光纤（DCF）•色散位移光纤（DSF）1.3um～1.55um•非零色散位移光纤（NZ-DSF）色散－群速度色散（脉冲展宽），偏振模色散，主要讨论群速度色散。 9.1色散引起的脉冲展宽•基本传输方程单模光纤中不同频率分量与传输距离关系：G（z，w）G（o，w）ej(w)z–频域：1–时域：g(z,t)G(z,w)dw2色散是不同频率的光在传输媒体中具有不同的群速度，将单模光纤中模式的相位系数在中心频率附近展开。 (w)n(w)/c"(ww)""(ww)200011dmm"""(ww)3(ww)20m06m!dw1dw群速率V＝g"d群速率色散系数(GVD)：""系数是脉冲展宽的主要因素(GVD:GroupVelocityDispersion） d1d22c色散系数D""dVddw2g:光波长：相位系数V：群速率w：频率g 保留三项:(w)n(w)/c1"(ww)""(ww)"""(ww)3000061(ww)(ww)(ww)301020306:群速率：群速度色散系数122c：色散斜率D3222c4cd3S()2()233333dw •高斯脉冲输入在载波波长远离零色散波长时，起主要作用的是：即群速度2色散：此时，10((w)ww2)30122且：G(z,w)G(0,w)ej(w)z的包络可12jw2表示为：A（z,w）＝A（0,z）e2 对于高斯输入初始脉冲为：1jct2[()]A(o,t)Ae2T00由傅里叶变换得：222wT02T[]A(o,w)A(0)V2e2(1jc)001jc2221wT0122T[]jw2则：A(z,w)A(0)2e2(1jc)201jc 反傅里叶变换2(1jc)t[]2AT2[T0j2z(1jc)]A(z,t)[00]e1[T2jz(1jc)]202高斯脉冲输入时在传输过程中仍保持高斯形状，但是脉冲宽度随z而改变Tczz1而且：1[(12)2(2)2]2TT2T2000T是光纤输出脉冲强度1点的强度，与T定义类似10 对c＝02Tz21T1[1()]2L0色散长度DTL20DT当z0时，12脉冲宽了2倍T012Tczc1对于c0,1[(12z)2(2)2]2[122z2(c21)z2]2TT2T2T2T200100T2c(1)2az2bzca2(c21)b2c1TT2T2000 T1T1T0T1201zc0e022cTz[]L时，1取最小2D1cT2 (w)n(w)/c1"(ww)""(ww)"""(ww)3000061(ww)(ww)(ww)301020306:群速率：群速度色散系数122c：色散斜率D3222c4cd3S()2()233333dw 9.2色散对系统性能的限制•对系统比特率限制•工作波长,远离零色散波长031BLD•对于零色散波长附4近，色散对零色散波0长光纤系统的比特率限制22cBLS21S()2823 •对系统传输距离的限制1L直接调制4BD＝0.15nmB＝2.5Gb/sD16ps/kmnm1L外调制16B2220ps2/kmB2.5Gb/s2典型值L500km 9.3色散补偿技术•后补偿技术j2(w2z)A(w,z）A(w,0)e2相干检测接收系统：H(w)exp(j(ww)2LF22直接检测接收系统：非线性均衡方法 •前补偿技术A（ow）A(w,0)exp(-jw2L)22•预啁啾技术条件：2<<0•调制•光放大器产生啁啾•光纤引入啁啾 •负色散DCF补偿在具有正色散值的标准单模光纤单元后接入一段在该波长下具有负色散特性的色散补偿光纤"(-jw2I1)(-jw2I2)A（z,w）A(w,0)e212e222j2w(21I122I2)2"A(0,w)e2ejw21z/2条件：zz0121222 •光滤波器补偿方法9.4色散管理•长距离系统色散管理，进行最佳设计，使GVD在光纤线路上具有最佳分布使系统性能最好•动态色散管理WDM系统'