高一数学必修1函数总复习课件PPT课件.ppt 112页

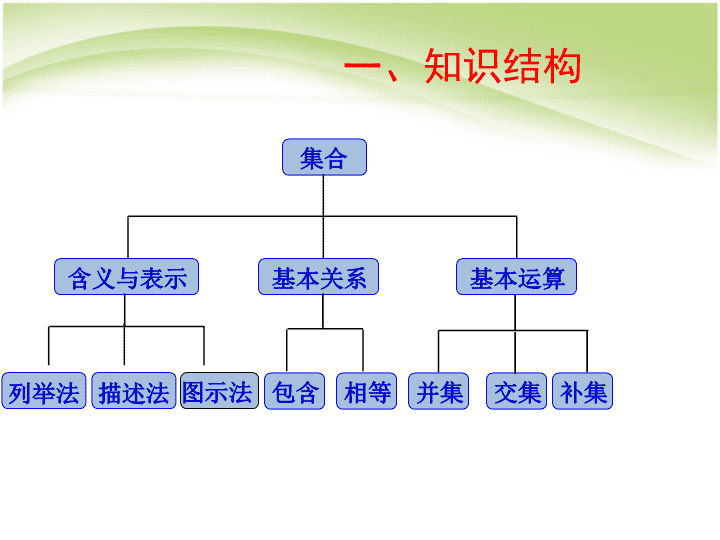
'高一数学必修1函数总复习课件 数与形,本是相倚依焉能分作两边飞数无形时少直觉形少数时难入微数形结合百般好隔离分家万事休切莫忘,几何代数统一体永远联系莫分离——华罗庚 集合基本关系含义与表示基本运算列举法描述法包含相等并集交集补集图示法一、知识结构 三、集合的并集、交集、全集、补集全集：某集合含有我们所研究的各个集合的全部元素，用U表示AB 0或2题型示例考查集合的含义 考查集合之间的关系 考查集合的运算 123453 返回 1.设,其中,如果，求实数a的取值范围扩展提升 2.设全集为R，集合，（1）求：A∪B，CR(A∩B)；（数轴法）（2）若集合,满足，求实数a的取值范围。 {}211-，，=M2.已知集合集合则M∩N是()AB{1}C{1，2}DΦ{}，，MxxyyNÎ==2练习1.集合A={1,0,x},且x2∈A,则x＝。3.满足{1,2}A{1,2,3,4}的集合A的个数有个-1B3 函数定义域奇偶性图象值域单调性函数的复习主要抓住两条主线1、函数的概念及其有关性质。2、几种初等函数的具体性质。二次函数指数函数对数函数反比例函数一次函数幂函数 函数函数的概念函数的基本性质函数的单调性函数的最值函数的奇偶性函数知识结构 BCx1x2x3x4x5y1y2y3y4y5y6A函数的三要素：定义域，值域，对应法则A.B是两个非空的数集,如果按照某种对应法则f，对于集合A中的每一个元素x，在集合B中都有唯一的元素y和它对应，这样的对应叫做从A到B的一个函数。一、函数的概念：思考:函数值域与集合B的关系 二、映射的概念设A,B是两个非空的集合,如果按照某种确定的对应关系f,使对于集合A中的任意一个元素x,在集合B中都有唯一确定的元素y于之对应,那么就称对应f:A→B为集合A到集合B的一个映射映射是函数的一种推广,本质是:任一对唯一 函数的定义域：使函数有意义的x的取值范围。求定义域的主要依据1、分式的分母不为零.2、偶次方根的被开方数不小于零.3、零次幂的底数不为零.4、对数函数的真数大于零.5、指、对数函数的底数大于零且不为1.6、实际问题中函数的定义域 （一）函数的定义域1、具体函数的定义域1.【-1,2）∪（2，+∞）2.（-∞，-1）∪（1，+∞）3.（3∕4,1】 练习： 2、抽象函数的定义域1）已知函数y=f(x)的定义域是[1，3]，求f(2x-1)的定义域2）已知函数y=f(x)的定义域是[0，5)，求g(x)=f(x-1)-f(x+1)的定义域3)1.[1,2];2.[1,4);3.[-] 思考：若值域为R呢？分析：值域为R等价为真数N能取（0，+∞）每个数。当a=0时，N=3只是（0，+∞）上的一个数，不成立；当a≠0时，真数N取（0，+∞）每个数即 求值域的一些方法：1、图像法，2、配方法，3、分离常数法，4、换元法，5单调性法。1)2)3)4) 三、函数的表示法1、解析法2、列表法3、图象法 例10求下列函数的解析式待定系数法换元法 （5）已知：对于任意实数x、y，等式恒成立，求赋值法构造方程组法(4)已知,求的解析式配凑法 增函数、减函数、单调函数是对定义域上的某个区间而言的。注意三、函数单调性定义：一般地，设函数f(x)的定义域为I：如果对于定义域I内某个区间D上的任意两个自变量x1、x2，当x1f(x2)，那么就说函数在区间上是减函数。区间D叫做函数的减区间。 写出常见函数的单调区间并指明是增区间还是减区间１、函数的单调区间是2、函数y=ax+b（a≠0）的单调区间是3、函数y=ax2+bx+c（a≠0）的单调区间是 用定义证明函数单调性的步骤:(1)设元，设x1,x2是区间上任意两个实数，且x1＜x2;(2)作差，f(x1)－f(x2);(3)变形，通过因式分解转化为易于判断符号的形式(4)判号，判断f(x1)－f(x2)的符号；（5）下结论. 1.函数f(x)=2x+1,(x≥1)４－x,(x＜1)则f(x)的递减区间为()A.[1,＋∞)B.(－∞,1)C.(0,＋∞)D.(－∞,0]B2、若函数f(x)=x2+2(a-1)x+2在区间[4,+∞)上是增函数,求实数a的取值范围小试身手？3判断函数的单调性。 拓展提升复合函数的单调性复合函数的定义：设y=f(u)定义域A，u=g(x)值域为B，若AB，则y关于x函数的y=f[g(x)]叫做函数f与g的复合函数，u叫中间量 复合函数的单调性复合函数的单调性由两个函数共同决定；引理1：已知函数y=f[g(x)]，若u=g(x)在区间(a,b)上是增函数，其值域为(c,d),又函数y=f(u)在区间(c,d)上是增函数，那么，原复合函数y=f[g(x)]在区间(a,b)上是增函数。x增→g(x)增→y增:故可知y随着x的增大而增大引理2：已知函数y=f[g(x)]，若u=g(x)在区间(a,b)上是减函数，其值域为(c,d),又函数y=f(u)在区间(c,d)上是减函数，那么，原复合函数y=f[g(x)]在区间(a,b)上是增函数。x增→g(x)减→y增:故可知y随着x的增大而增大 复合函数的单调性若u=g(x)增函数减函数增函数减函数y=f(u)增函数减函数减函数增函数则y=f[g(x)]增函数增函数减函数减函数规律：当两个函数的单调性相同时，其复合函数是增函数；当两个函数的单调性不相同时，其复合函数是减函数。“同增异减” 复合函数的单调性例题：求下列函数的单调性y=log4(x2－4x+3)解　设y=log4u（外函数）,u=x2－4x+3（内函数）.由u＞0,u=x2－4x+3，解得原复合函数的定义域为{x|x＜1或x＞3}.当x∈(－∞，1)时，u=x2－4x+3为减函数，而y=log4u为增函数，所以(－∞，1)是复合函数的单调减区间；当x∈(3，±∞)时，u=x2－4x+3为增函数y=log4u为增函数，所以，(3，+∞)是复合函数的单调增区间. 解：设u=x2－4x+3，u=x2－4x+3=(x－2)2－1,x＞3或x＜1，(复合函数定义域)x＜2　(u减)解得x＜1.所以x∈(－∞，1)时，函数u单调递减.由于y=log4u在定义域内是增函数，所以由引理知：u=(x－2)2－1的单调性与复合函数的单调性一致，所以(－∞，1)是复合函数的单调减区间.u=x2－4x+3=(x－2)2－1,x＞3或x＜1，(复合函数定义域)x＞2　(u增)解得x＞3.所以(3，+∞)是复合函数的单调增区间.代数解法： 解:　设y=logu,u=2x－x2.由u＞0,u=2x－x2解得原复合函数的定义域为0＜x＜2.由于y=log13u在定义域(0，+∞)内是减函数，所以，原复合函数的单调性与二次函数u=2x－x2的单调性正好相反.易知u=2x-x2=-(x－1)2+1在x≤1时单调增.　　　　由　0＜x＜2（复合函数定义域）x≤1，(u增)解得0＜x≤1,所以(0，1］是原复合函数的单调减区间.又u=－(x－1)2+1在x≥1时单调减，由x＜2，　(复合函数定义域)x≥1，　(u减)解得0≤x＜2,所以[0，1＝是原复合函数的单调增区间.例2　求下列复合函数的单调区间：y=log(2x－x2) 例题：求函数的单调性。解：设，f(u)和u(x)的定义域均为R因为，u在上递减，在上递增。而在R上是减函数。所以，在上是增函数。在上是减函数。 例4：求的单调区间.解:　设由u∈R,u=x2－2x－1,解得原复合函数的定义域为x∈R.因为在定义域R内为减函数，所以由二次函数u=x2－2x－1的单调性易知,u=x2－2x－1=(x－1)2－2在x≤1时单调减，由x∈R,　　(复合函数定义域)x≤1，　(u减)解得x≤1.所以(－∞，1］是复合函数的单调增区间.同理［1，+∞)是复合函数的单调减区间. 复合函数的单调性小结复合函数y=f[g(x)]的单调性可按下列步骤判断：(1)将复合函数分解成两个简单函数：y=f(u)与u=g(x)。其中y=f(u)又称为外层函数,u=g(x)称为内层函数;(2)确定函数的定义域；(3)分别确定分解成的两个函数的单调性；(4)若两个函数在对应的区间上的单调性相同（即都是增函数，或都是减函数），则复合后的函数y=f[g(x)]为增函数；(5)若两个函数在对应的区间上的单调性相异（即一个是增函数，而另一个是减函数），则复合后的函数y=f[g(x)]为减函数。复合函数的单调性可概括为一句话：“同增异减”。 四、函数的奇偶性1.奇函数:对任意的,都有2.偶函数:对任意的,都有3.奇函数和偶函数的必要条件:注:要判断函数的奇偶性,首先要看其定义域区间是否关于原点对称!定义域关于原点对称. 奇(偶)函数的一些特征1.若函数f(x)是奇函数,且在x=0处有定义,则f(0)=0.2.奇函数图像关于原点对称,且在对称的区间上不改变单调性.3.偶函数图像关于y轴对称,且在对称的区间上改变单调性 例12判断下列函数的奇偶性 函数的图象1、用学过的图像画图。2、用某种函数的图象变形而成。（1）关于x轴、y轴、原点对称关系。（2）平移关系。（3）绝对值关系。 反比例函数1、定义域.2、值域3、图象k>0k<0 二次函数1、定义域.2、值域3、图象a>0a<0 指数函数1、定义域.2、值域3、图象a>10100)的性质及应用 .函数(a>0)的大致图像xy0 获取新知利用所掌握的函数知识,探究函数(a>0)的性质.1.定义域2.奇偶性(-∞,0)∪(0,+∞)奇函数f(-x)=-f(x) 3.确定函数(a>0)的单调区间⑴.当x∈(0,+∞)时,确定某单调区间 ⑵.当x∈(-∞,0)时,确定某单调区间综上,函数(a>0)的单调区间是单调区间的分界点为:a的平方根 4.函数(a>0)的大致图像xy0 5.函数(a>0)的值域 运用知识1.已知函数 2.已知函数,求f(x)的最小值,并求此时的x值. 3.建筑一个容积为800米3,深8米的长方体水池(无盖).池壁,池底造价分别为a元/米2和2a元/米2.底面一边长为x米,总造价为y.写出y与x的函数式,问底面边长x为何值时总造价y最低,是多少? 函数图象与变换1．平移变换(1)水平方向的变换：y＝f(x＋a)的图象可由y＝f(x)的图象沿x轴向左平移(a>0)或向右平移(a<0)|a|个单位而得到．(2)竖直方向的变换：y＝f(x)＋b的图象可由y＝f(x)的图象沿y轴向上平移(b>0)或向下平移(b<0)|b|个单位而得到． 2．对称变换(1)y＝f(x)与y＝f(－x)的图象关于y轴对称．(2)y＝f(x)与y＝－f(x)的图象关于x轴对称．(3)y＝f(x)与y＝－f(－x)的图象关于原点对称．(4)y＝|f(x)|的图象是保留y＝f(x)图象中位于x轴上方的部分及与x轴的交点，将y＝f(x)的图象中位于x轴下方的部分翻折到x轴上方去而得到．(5)y＝f(|x|)的图象是保留y＝f(x)中位于y轴右边部分及与y轴的交点，去掉y轴左边部分而利用偶函数的性质，将y轴右边部分以y轴为对称轴翻折到y轴左边去而得到． (2)先作函数y＝x2－2x的位于x轴上方的图象，再作x轴下方图象关于x轴对称的图象，得函数y＝|x2－2x|的图象，如图所示． (3)先作函数y＝x2－2x位于y轴右边的图象，再作关于y轴对称的图象，得到函数y＝x2－2|x|的图象，如图所示． 例作函数的图象yxo1yxo1 抓住函数中的某些性质，通过局部性质或图象的局部特征，利用常规数学思想方法（如类比法、赋值法添、拆项等）。高考题和平时的模拟题中经常出现。抽象性较强；综合性强；灵活性强；难度大。没有具体给出函数解析式但给出某些函数特性或相应条件的函数概念题型特点解题思路抽象函数问题 一、研究函数性质“赋值”策略对于抽象函数，根据函数的概念和性质，通过观察与分析，将变量赋予特殊值，以简化函数，从而达到转化为要解决的问题的目的。 (1)令x=…,-2,-1,0,1,2,…等特殊值求抽象函数的函数值；(3)令y=-x,判断抽象函数的奇偶性；(4)换x为x+T,确定抽象函数的周期；(2)令x=x2,y=x1或y=,且x10且）y=logax(a>0且）同上 一、一次函数模型:f(x+y)=f(x)+f(y)解：例1: 解法2： 例2：解： 二.指数函数模型:f(x+y)=f(x)•f(y)例3:求证:证明： 三.对数函数模型：f(x•y)=f(x)+f(y)例4：解： 内容小结以上列举了求解抽象型函数问题的常规解题思想，当然对于用常规思想难以解决的数学问题，若利用一些特殊的数学思想方法求解，如合理赋值、类比联想;添、拆项;归纳猜想等等。处理这类问题时，常需将几种解题思想综合运用，"多管齐下"。通过抽象型函数问题的解题思想的探求，提高解题能力，培养思维的灵活性，最终达到创新思想的培养。 固有频率的单跨转子实验台设计第五组95 实验要求1.了解(或测量)实验台和转子的尺寸,计算其固有频率。2.测试转子系统的振动，了解固有频率振动现象。3.了解测试系统，学习NILabview软件的编写。4.应用Labview软件编写简单的信号采集程序，并程序的编写情写入课程设计报告中。96 设计要求1:固有频率计算（15hz）2:转子的设计和圆盘的设计,要求有零件图纸3:总的设计装配图4:驱动功能部件的选择和确定5:单跨转子部分的轴承型号的选择6:设计轴的强度核定97 设计要求：固有频率为15Hz的单跨转子实验台；轴的截面惯性矩：轴的弹性系数：固有频率：中点98 固有频率计算（15hz）转盘的质量m=3.9kg转盘直径d=8mm经计算L=380mm99 铁的密度为已知d=8mm,m=3.9kg取b1=90mm,b2=60mm,D1=38mm,得D2=100mm100 101 102 103 电机选择和杆的强度校和随着现代化工业的发展,越来越多的新型电机不断研制出来。转矩和转速是电机最重要的两个参数,要合理地选用电机,必须要准确地对转矩和转速进行测量电机转矩和转速的测量方法及传感器的选择电机转矩的测量方法:转矩的测量,可分为传递法、平衡力法及能量转化法。电气式分为发电机式、电涡流式等,精度较高。机械结构对测量稳定性的影响测量是靠机械传动来实现的,因为传感器极易受工作环境的影响,所以机械传动结构是测量误差的重要来源。在设计转矩和转速测量仪时必须对这两方面影响给与足够的重视。104 传感器轴的确定:根据所要求的固有频率，可以得知船东杆所受转矩的要求，所以必须首先保证传感器轴具有一定的强度。如果待测是三相电机,启动时转矩为额定转矩2～3倍,为避免过载可能造成的传感器永久性破坏,测量裕度取量程的3倍,传感器扭轴所受的转矩T传，对于实心轴,由强度条件τmax=T传/Wn≤[τ许用],Wn=πd3/16，可计算得d=9.7mm.其中τmax为最大理论扭矩,Wn抗扭截面模量,τ许用为许用剪应力,d为传感器轴直径。其次,为了使传感器具有一定的灵敏度,在保证强度的情况下,应选择适当的刚度,所以取轴的直径d=10mm。对于所要求的电机测量范围为0～900r/min（15hz）的要求,且为了保证安全测量,取转速测量裕度为0～1500r/min.只要轴临界转速大于转换到传感器轴的等效转速,和扭矩即满足设计要求。由计算得,轴临界转速远大于等效转速,故所选的传感器轴满足工作需要。根据以上要求，我们选择45SL5H4型号电机105 实验设备使用的实验设备有：电机、轴承支架*2、单跨转子、变频器、连轴器、开关电源（提供-24V电压给电涡流传感器）、USB5935AD数据采集器106 107 Labview简介LabVIEW是一种程序开发环境，由美国国家仪器（NI）公司研制开发的，类似于C和BASIC开发环境，但是LabVIEW与其他计算机语言的显著区别是：其他计算机语言都是采用基于文本的语言产生代码，而LabVIEW使用的是图形化编辑语言G编写程序，产生的程序是框图的形式。它主要的方便就是，一个硬件的情况下，可以通过改变软件，就可以实现不同的仪器仪表的功能，非常方便，是相当于软件即硬件！现在的图形化主要是上层的系统，国内现在已经开发出图形化的单片机编程系统（支持32位的嵌入式系统，并且可以扩展的），不断完善中(大家可以搜索CPUVIEW会有更详细信息；）108 Labview程序框图109 Labview实验结果110 小组成员赵辰伟07110228苑帅07110229陈欣07110230冯逸07110231刁仲达07110236薛佳卫0710237范腾07110238陆海华07110239111 完112'