最新5.《圆、相交线与平行线》解析课件PPT.ppt 53页

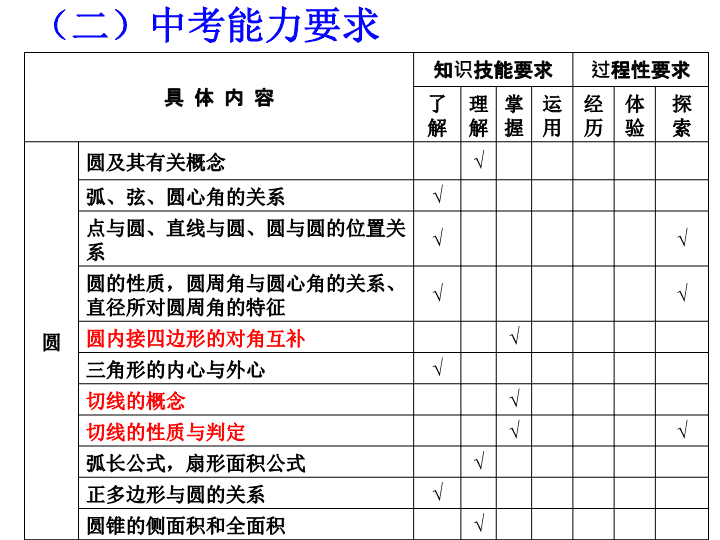
'5.《圆、相交线与平行线》解析 一、课标与中考要求（一）课标要求（1）理解圆、弧、弦、圆心角、圆周角的概念，了解等圆、等弧的概念；探索并了解点与圆的位置关系。（2）探索并证明垂径定理：垂直于弦的直径平分弦以及弦所对的两条弧。（3）探索圆周角与圆心角及其所对弧的关系，了解并证明圆周角定理及其推论：圆周角的度数等于它所对弧上的圆心角度数的一半；直径所对的圆周角是直角；90°的圆周角所对的弦是直径；圆内接四边形的对角互补。（4）知道三角形的内心和外心。（5）了解直线和圆的位置关系，掌握切线的概念。探索切线与过切点的半径的关系，会用三角尺过圆上一点画圆的切线。（6）探索并证明切线长定理：过圆外一点所画的圆的两条切线长相等。（7）会计算圆的弧长、扇形的面积。（8）了解正多边形的概念及正多边形与圆的关系。 （二）中考能力要求具体内容知识技能要求过程性要求了解理解掌握运用经历体验探索圆圆及其有关概念√弧、弦、圆心角的关系√点与圆、直线与圆、圆与圆的位置关系√√圆的性质，圆周角与圆心角的关系、直径所对圆周角的特征√√圆内接四边形的对角互补√三角形的内心与外心√切线的概念√切线的性质与判定√√弧长公式，扇形面积公式√正多边形与圆的关系√圆锥的侧面积和全面积√ 五、复习目标1、系统熟悉圆的有关概念；2、巩固圆的有关性质和定理；3、进一步掌握应用圆的有关知识解决某些数学问题。 六、教学内容和设计（一）课时安排本讲内容虽多，但是属于上学期重点内容，学生对这部分基本知识仍有记忆，所以在一轮复习中，计划进行知识整合，分3课时完成。第1课时：知识复习（包含：圆的的有关性质、与圆有关的位置关系、与圆有关的计算）第2课时：章节检测（主要针对考点及复习过程中学生的遗忘点进行命题检测）第3课时：讲评与拔高 （二）教学内容（一）真题再现1、（2013•德州）如图，扇形AOB的半径为1，∠AOB=90°，以AB为直径画半圆，则图中阴影部分的面积为（　　）A．B．C．D．2、（2014·德州）如图，⊙O的直径AB为10cm，弦BC为5cm，D、E分别是∠ACB的平分线与⊙O，AB的交点，P为AB延长线上一点，且PC=PE．（1）求AC、AD的长；（2）试判断直线PC与⊙O的位置关系，并说明理由． （二）教学内容圆的有关性质圆的有关概念圆的对称性圆周角定理及其推论垂径定理及其推论圆心角、弧、弦之间关系圆内接四边形的性质与圆有关的计算正多边形与圆弧长扇形面积圆锥的侧面积与全面积与圆有关的位置关系点与圆的位置关系直线与圆的位置关系圆与圆的位置关系切线的性质与判定切线长定理三角形的内切圆圆（二）知识框架 （二）教学内容（三）复习目标1、系统熟悉圆的有关概念；2、巩固圆的有关性质和定理；3、进一步掌握应用圆的有关知识解决某些数学问题。 (四)典例分析弧、弦、圆心角的关系A（二）教学内容 【方法规律技巧】在应用弧、弦、圆心角之间的关系定理及推论时，首先要弄清楚要求证的是哪组量相等，然后只要在除改组量之外的两组量中找一组量证明他们想等即可。通常通过作辅助线构造所需证明的量，常作的辅助线是半径及圆心到弦的距离，此时与垂径定理综合应用。 【典例设计】垂径定理及其推论例2：如图，AB为⊙O的直径，弦CD⊥AB于E，已知CD＝12，BE＝2，则⊙O的直径为()A、8B、10C、16D、20【分析】连接OC，即可证得△OEC是直角三角形，根据垂径定理即可求得OC，进而求出AB的长。D 【方法规律技巧】垂径定理是圆的重要定理之一，是证明圆中线段相等、角相等以及垂直关系的重要依据。在解决与弦、弧的中点有关的问题时，常连接圆心和中点，或过圆心作弦的垂线，以利用垂径定理构造直角三角形解决问题。 【典例设计】例3：如图，AB是⊙O的直径，AP是⊙O的切线，A是切点，BP与⊙O交于点C．(1)若AB＝2，∠P＝30°，求AP的长；(2)若D为AP的中点，求证：直线CD是⊙O的切线．【分析】(1)由切线的性质可知PA⊥AB，再在Rt△BAP中，通过∠P的正切或应用勾股定理求解；(2)欲证直线CD是⊙O的切线，只需连接OC，证明OC⊥CD即可．连接AC，由圆周角性质得到Rt△ACP，根据直角三角形斜边上中线等于斜边一半得CD＝AD，再利用等腰三角形性质即可证∠OCD＝∠OAD＝90°。切线的性质与判定 【方法规律技巧】证明切线时，可以分以下情况进行证明：（1）若已知直线与圆的公共点，则采用判定定理法，其基本思路是：当已知点在圆上时，连接过这点的半径，证明这条半径与直线垂直即可。可简述为：有切点，连半径，证垂直。（2）若未知直线与圆的交点，则采用数量关系法，其基本思路是：过圆心作直线的垂线段，证明垂线段的长度等于圆的半径。可简述为：无切点，作垂线，证相等。 【典例设计】求阴影部分的面积例4：（2014•德州）如图，正三角形ABC的边长为2，D、E、F分别为BC、CA、AB的中点，以A、B、C三点为圆心，半径为1作圆，则圆中阴影部分的面积是． 【方法规律技巧】运用扇形的面积公式求阴影部分的面积，一般地可以采取将阴影部分的面积看作几个几何图形面积的和差的方法来进行计算。 （二）教学内容圆的有关性质圆的有关概念圆的对称性圆周角定理及其推论垂径定理及其推论圆心角、弧、弦之间关系圆内接四边形的性质与圆有关的计算正多边形与圆弧长扇形面积圆锥的侧面积与全面积与圆有关的位置关系点与圆的位置关系直线与圆的位置关系圆与圆的位置关系切线的性质与判定切线长定理三角形的内切圆圆（五）自我梳理 （二）教学内容（六）达标检测1、已知正n边形的一个内角为135°，则边数n的值是()A．6B．7C．8D．102、（2014•枣庄）如图，将四个圆两两相切拼接在一起，它们的半径均为1cm，则中间阴影部分的面积为cm2．3、（2014·南通）如图，点A、B、C、D在⊙O上，O点在∠D的内部，四边形OABC为平行四边形，则∠OAD+∠OCD=。4、（2014·陕西）如图，⊙O的半径为4，B是⊙O外一点，连接OB，且OB=6，过点B作⊙O的切线BD，切点为D，延长BO交⊙O于点A，过点A作切线BD的垂线，垂足为C．（1）求证：AD平分∠BAC；（2）求AC的长． 七、教学反思圆是初中几何中相当重要的一节，对于本节课的复习，我觉得提炼方法，形成知识体系是至观重要的：圆有哪些性质？三大性质定理学生首先要明确，以及各自适用的的题型。点与圆、线与圆、圆与圆的关系分别是什么？有关的题型又是什么？在讲课时通过典型的代表性的题目的讲练结合，学生可以通过解题后的反思提炼方法，形成知识结构，加深了对定理的理解。复习不是知识的简单再现，在复习过程中，教师也应是坚持启发引导学生发现思维误区，总结方法为主，辅之以精讲。充分发扬教学民主，给学生以足够的思维空间，对于解题思路的探讨过程，让学生真正理解，从而提高复习质量和复习效率。 相交线与平行线复习 一、课标与中考要求（一）课标要求（1）理解对顶角、余角、补角等概念，探索并掌握对顶角相等、同角（等角）的余角相等，同角（等角）的补角相等的性质。（2）理解垂线、垂线段等概念，能用三角尺或量角器过一点画已知直线的垂线。（3）理解点到直线的距离的意义，能度量点到直线的距离。（4）掌握基本事实：过一点有且只有一条直线与这条直线垂直。（5）识别同位角、内错角、同旁内角。（6）理解平行线概念；掌握基本事实：两条直线被第三条直线所截，如果同位角相等，那么两直线平行。（7）掌握基本事实：过直线外一点有且只有一条直线与这条直线平行。（8）掌握平行线的性质定理：两条平行直线被第三条直线所截，同位角相等。*了解平行线性质定理的证明。（9）能用三角尺和直尺过已知直线外一点画这条直线的平行线。（10）探索并证明平行线的判定定理：两条直线被第三条直线所截，如果内错角相等（或同旁内角互补），那么两直线平行；平行线的性质定理：两条平行直线被第三条直线所截，内错角相等（或同旁内角互补）。（11）了解平行于同一条直线的两条直线平行。 （二）中考能力要求具体内容知识技能要求过程性要求了解理解掌握运用经历体验探索相交线与平行线补角、余角、对顶角的概念√对顶角相等、同角或等角的余角（补角）相等√√垂线、垂线段的概念、画法及性质，点到直线的距离√√“过一点有且只有一条直线与已知直线垂直”√线段垂直平分线及性质√√同位角、内错角、同旁内角√平行线的概念√“过直线外一点有且只有一条直线与已知直线平行”√平行线的性质和判定√√平行线间的距离√√画平行线√ 二、五年命题分析年份题号题型分数考点20145选择题3平行线的性质、角平分线的性质20134选择题3平行线的性质、等腰三角形的性质20114选择题3平行线的性质、对顶角、三角形内角和定理20102选择题3平行线的性质、三角形外角的性质 三、考点解读相交线与平行线是“图形与几何”领域的基础知识，也是中考的常考内容，题型多以选择题、填空题为主，一般难度不大，属于基础性试题。其中，平行线的性质与判定是中考的重点考查内容之一，一般与三角形、四边形，圆等有关知识综合在一起考查较多。 四、备考策略备考时，要加强对概念的理解，掌握平行线的性质和判定。当两条平行线被第三条直线所截时，弄清哪条直线是第三条直线（即截线）是解答关键。 五、复习目标1、回顾相交线与平行线的性质及判定方法；2、运用相交线与平行线的性质及判定方法解题；3、灵活选择方法，综合使用知识解题。 六、教学内容和设计（一）课时安排本讲安排一课时完成复习。 （二）教学内容（一）真题再现1、（2010•德州）如图，直线AB∥CD，∠A＝70°，∠C＝40°，则∠E等于（）Ａ30°Ｂ40°C60°Ｄ70°2、（2011•德州）如图，直线l1∥l2，∠1=40°，∠2=75°，则∠3等于（）A55°B60°C65°D70°3、（2013•德州）如图，AB∥CD，点E在BC上，且CD=CE，∠D=74°，则∠B的度数为（）A．68°B．32°C．22°D．16°4、（2014•德州）如图，AD是∠EAC的平分线，AD∥BC，∠B=30°，则∠C为（）A．30°B．60°C．80°D．120° （二）教学内容（二）知识框架相交线平行线两条直线相交两条直线被第三条直线所截平行公理及其推理对顶角平移的特征邻补角平移对顶角相等邻补角互补垂直定义垂线段最短点到直线的距离同位角、内错角、同旁内角平行线的判定两条平行线之间的距离平行线的性质特殊情况一般情况垂直直线与直线之间的位置关系 （二）教学内容（三）复习目标1、回顾相交线与平行线的性质及判定方法；2、运用相交线与平行线的性质及判定方法解题；3、灵活选择方法，综合使用知识解题。 题型一：考查基本概念的问题。例1：点P为直线l外一点，点A、B、C三点在直线l上，且PA＝3cm，PB＝4cm，PC＝5cm，则点P到直线l的距离为()A．3cmB．4cmC．5cmD．不大于3cm例2：(2014济南）如图，点Ｏ在直线AB上，若，则的度数是A.50◦B．60◦C.140◦D．150◦紧扣概念是关键。(四)典例分析（二）教学内容 题型二：相交线、平行线问题中角的求法。例3、如图，已知∠1＝∠2，∠3＝80°，则∠4＝________.A．80°B．70°C．60°D．50°例4：（2014•威海）直线l1∥l2，一块含45°角的直角三角板如图放置，∠1=85°，则∠2=．例5：(2014年山东淄博)如图，直线a∥b，点B在直线上b上，且AB⊥BC，∠1=55°，求∠2的度数．解答与相交线、平行线有关的角的计算问题，弄清两条平行线到底是哪条直线所截是关键，有时因弄不清第三条直线而出错。 题型三：平行线问题中辅助线的作法。例6．已知：如图，AB∥CD，求证：∠ABE+∠CDE=∠BED.变式1：已知：如图，AB∥CD，求证：∠BED=360°-（∠ABE+∠CDE）.变式2.已知：如图，AB∥CD，求证：∠BED=∠ABE-∠CDE变式3.已知：如图，AB∥CD，求证：∠BED=∠CDE-∠ABE变式图形方法归纳：解答平行线问题时，所作的辅助线主要是作出一条合适的平行线，以便将已知诸条件有机的联系起来。 例7：(2014年山东淄博)如图，矩形纸片ABCD中，点E是AD的中点，且AE=1，BE的垂直平分线MN恰好过点C．则矩形的一边AB的长度为（）A、1B．2C．D．题型四：垂直平分线问题的计算与证明。分清直线和线段 题型五：与其它知识点相结合的问题。例8：（2014•临沂）如图，在⊙O中，AC∥OB，∠BAO=25°，则∠BOC的度数为（）A．25°B．50°C．60°D．80° （二）教学内容（五）查漏补缺相交线平行线两条直线相交两条直线被第三条直线所截平行公理及其推理对顶角平移的特征邻补角平移对顶角相等邻补角互补垂直定义垂线段最短点到直线的距离同位角、内错角、同旁内角平行线的判定两条平行线之间的距离平行线的性质特殊情况一般情况垂直直线与直线之间的位置关系 1、下图能说明∠1＞∠2的是()2、如图，是我们学过的用直尺和三角尺画平行线的方法示意图，画图的原理是：A．同位角相等，两直线平行B．内错角相等，两直线平行C．两直线平行，同位角相等D两直线平行，内错角相等．3、如图，直线l∥m∥n，等边△ABC的顶点B、C分别在直线n和m上，边BC与直线n所夹锐角为25°,则∠α的度数为（）A．25°B．45°C.35°D.30°（二）教学内容（六）达标检测 4、（2014•枣庄）如图，AB∥CD，AE交CD于C，∠A=34°，∠DEC=90°，则∠D的度数为（）A17°B34°C56°D．124°5、（2014•临沂）如图，已知l1∥l2，∠A=40°，∠1=60°，则∠2的度数为（　　）A．40°B．60°C．80°D．100°6、（2014•聊城）如图，将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上，如果∠1=27°，那么∠2的度数为（　　）A．53°B．55°C．57°D．60° 7、一大门的栏杆如图所示，BA垂直于地面AE于A，CD平行于地面AE，则∠ABC＋∠BCD＝________度．8、（2014年日照市）如图，AB是⊙O的直径，AM和BN是它的两条切线，DE切⊙O于点E，交AM于点D，交BN于点C，（1）求证：OD∥BE；（2）如果OD=6cm，OC=8cm，求CD的长．（8题图）NEBCOAMD 七、教学反思相交线与平行线在中考中虽直接考查的题目较为简单，但在平面几何计算和证明中，应用十分广泛，对学生分析问题的能力、综合解题的能力要求也是较高的。在备考复习过程中也不能降低对学生的要求，教师要注意对学生思维进行引导。 硬膜下积液聂文彬 硬膜下积液（subduralfluidaccumulation）又称硬膜下水瘤，多是外伤后硬膜下腔出现的脑脊液积聚。常发生于一侧或两侧额颞部，以双侧额部为多见。分为急性和慢性，急性在数小时内形成（少见），慢性者数天或数周。定义 硬膜蛛网膜软膜形成原因脑脊液 积液多发生于枕部着地，原发性颅脑损伤患者。积液多在幕上额颞区，多发生受力的对冲部位。原发性颅脑损伤较轻者，伤后可无意识障碍，随着积液的增多而出现昏迷或意识障碍加深。慢性硬膜下积液的临床症状不明显，常常被漏诊或误诊。临床特点 积液常有被膜包裹，CT片上呈新月形低密度影影像学表现 大面积脑梗死后，大脑半球灌注极差，导致脑组织坏死，萎缩。形成双侧硬膜下积液。脑梗塞后硬膜下积液 三个月后复查脑梗死后硬膜下积液 如果没有颅内压增高的临床症状，硬膜下积液不需要处理，会慢慢吸收慎用或不用脱水剂，以免颅压过低导致积液增多。有的可转为慢性血肿。动态观察积液量是否增加，复查颅脑CT。保守治疗 临床上有神经系统压迫症状或有癫痫发作者。幕上积液量>25ml者，幕下>8ml，手术治疗利于病情恢复。占位效应较重，有明显的颅高压症状，影像学检查（CT或MRI）示脑室、脑池受压、变形，中线移位>10mm者。手术指征 互学互长'