最新北宋建立及其制度创设(精)课件PPT.ppt 23页

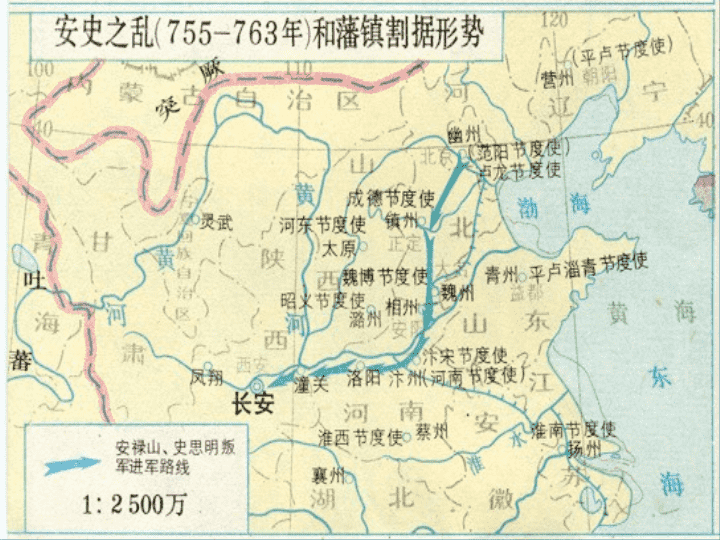
'北宋建立及其制度创设(精) 建隆二年（961），太祖召赵普问曰：“天下自唐季以来，数十年间，帝王凡易八姓，战斗不息，生民涂地，其故何也？吾欲息天下之兵，为国家长久计，其道何如？”普曰：“……此非他故，方镇太重，君弱臣强而已。今所以治之，亦无他奇巧，惟稍夺其权，制其钱谷，收其精兵，则天下自安矣。”语未毕，上曰：“卿勿复言，吾已喻矣！”——《续资治通鉴长编》卷二二、宋朝的“防弊”之制——文官体制 收其精兵——内重外轻全国精锐部队悉集于禁军，禁军的布置采取。“强干弱枝”、“守内虚外”策略，20余万禁军之中，京师附近驻扎10余万，地方分驻10余万。 收其精兵——以文制武侍卫亲军步军都指挥使司侍卫亲军马军都指挥使司武将殿前都指挥使司三衙枢密副使文臣枢密使枢密院范祖禹：“天下之兵，本于枢密，有发兵之权而无握兵之重，京师之兵，总于三帅，有握兵之重而无发兵之权。上下相维，不得专制。”——《范太史集》卷二六《论曹诵札子》 北宋初年发生了这样一件事：963年，宋太祖任命京官周渭到永济任知县。周渭到任时，大将符彦卿亲往城外迎接，但周渭却趾高气扬，仅在马上拱手作揖。见此情景，平日专横跋扈的符彦卿心中极为不满，却又无可奈何。 稍夺其权——重文轻武1、通过科举制度，提拔大量文人担任官职。“满朝朱紫贵,尽是读书人”——《神童诗》北宋汪洙2、中央政府要员由文人担任，形成士大夫为主体的文官政府。宰相——同中书门下平章事；副相——参知政事军事——枢密使3、官、职、差遣分离制 官以寓禄秩、叙位著，职以待文学之选，而别为差遣以治内外之事。——《宋史·职官志（总序）》“居其官不知其职者，十常八九”——樊树志《国史概要》 考试制度和规则变化：1、分三级：解试、省试、殿试2、弥封、誊录制度，保证公平公正三、文官体制的保障——科举制的完善“惟有糊名公道在，孤寒宜向此中求。”——朱胜非引“前辈诗” 考试内容的变化：1、宋初进士考试：承唐以诗赋取人2、宋中期以后，废除帖经，增考策论（对儒家典籍的理解和对社会事务的分析能力）作用：1、为宋朝选拔了大量的文官人才2、有利于教育的普及和知识的传播 宋真宗时，文武百官9700人，宋仁宗时增至17000人，宋英宗时增至24000人，这还不包括正官之外等候差遣空缺的候补官僚，如果把他们也统计在内，那么数量将猛增数倍。——《国史概要》樊树志“一位未缺,十人竞逐,纡朱满路,袭紫成林”。——李焘《续资治通鉴长编》文官体制的影响 文官体制的影响 历代科举取士数额略计年数榜数取士总数年均取士唐290266660323（进士）宋320130正奏名60000+340（进士、诸科)特奏名50000元98161139（左右榜）12（进士）明277932462489（进士）清26811426888100（进士）《宝祐四年登科录》：是科录取进士601人。其中官僚出身184人，平民出身417人。 北宋武臣石像北宋文臣石像 中国福利会儿童计箅机活动中心计算机数学班讲义王指导2003-11数学欣赏(三) 握手问题一位先生说：“前些日子，我同我太太一起参加了一个宴会，酒席上还有另外四对夫妻。见面时，大家相互问候，亲切握手。当然，没有人会去同自己的太太握手，自己也不会同自己握手，与同一个人握过手之后，也不可能再同他或她进行第二次握手。彼此之间的握手全部结束之后，我好奇地询问在座的各位先生和女士，当然也包括我太太在内，每人各握过几次手?使我惊奇的是，每个人报出的握手次数竟完全不一样。请问：我太太同别人共握了几次手?”为了使这个问题的叙述更为严密，还需作如下说明：(1)甲与乙握手，在计算握手次数时，甲算一次，乙也算(2)握手并不要求一个都不漏，可握而未握的情况也是有的，例如，行注目礼，双手合掌，拍拍肩膀，对方正在与别人握手不便越位等等，这当然不算不礼貌。不过，这样一来就大大地增加了问题的复杂性，使问题似乎变得无从求解了。 解决这个问题，主要是运用逻辑推理。既然宴会上共有10人，任何人都不同自己握手，也不同自己的配偶握手，所以，任何一个人握手的次数最多只能等于8。由于这位先生已问过各位宾客，得知他们每人握手的次数都不一样，可见这9个人的握手次数必定是0，1，2，·3，4，5，6，7，8。显然，握手次数为8的那一位已同除了自己的配偶以外的每个人都握过丁手，所以，这个人(无法判定这个人是先生或女士)的配偶必定就是那个握手次数为0的人。由于这两个人的关系已被确定，于是就可以请他们退到“圈子”以外。接着可以推定，握手次数为?的人必定与握手次数为l的人是一对夫妻；握手次数为6的人必定与握手次数为2的人是一对夫妻；如此等等。 最后只剩下握手次数为4的人，可以断定，此人肯定是提出问题的那位先生的太太。解决问题之后，让我们再来回顾这道题目，对称性、递归性、消去法从这道题中都得到了很好的体现。怪不得一些评论冢们说：这样的数学题目，真是太“艺术化”了。此题的发明权，属于当代美国数学科普大师—马丁·家德纳。 '