最新北师大版八年级下册6.1平行四边形的性质(2)课件课件PPT.ppt 26页

'进入夏天，少不了一个热字当头，电扇空调陆续登场，每逢此时，总会想起那一把蒲扇。蒲扇，是记忆中的农村，夏季经常用的一件物品。　　记忆中的故乡，每逢进入夏天，集市上最常见的便是蒲扇、凉席，不论男女老少，个个手持一把，忽闪忽闪个不停，嘴里叨叨着“怎么这么热”，于是三五成群，聚在大树下，或站着，或随即坐在石头上，手持那把扇子，边唠嗑边乘凉。孩子们却在周围跑跑跳跳，热得满头大汗，不时听到“强子，别跑了，快来我给你扇扇”。孩子们才不听这一套，跑个没完，直到累气喘吁吁，这才一跑一踮地围过了，这时母亲总是，好似生气的样子，边扇边训，“你看热的，跑什么？”此时这把蒲扇，是那么凉快，那么的温馨幸福，有母亲的味道！　　蒲扇是中国传统工艺品，在我国已有三千年多年的历史。取材于棕榈树，制作简单，方便携带，且蒲扇的表面光滑，因而，古人常会在上面作画。古有棕扇、葵扇、蒲扇、蕉扇诸名，实即今日的蒲扇，江浙称之为芭蕉扇。六七十年代，人们最常用的就是这种，似圆非圆，轻巧又便宜的蒲扇。　　蒲扇流传至今，我的记忆中，它跨越了半个世纪，也走过了我们的半个人生的轨迹，携带着特有的念想，一年年，一天天，流向长长的时间隧道，袅北师大版八年级下册6.1平行四边形的性质(2)课件 八年级数学复习ADBC定义表示方法性质两组对边分别平行的四边形叫做平行四边形。其不相邻的两个顶点连成的线段叫它的对角线。平行四边形ABCD,记为“□ABCD”,读作“平行四边形ABCD”,其中线段AC,BD称为对角线。1.平行四边形是中心对称图形，两条对角线的交点是它的对称中心。2.平行四边形的两组对边分别平行且相等;3.平行四边形的对角相等，相邻两角互补。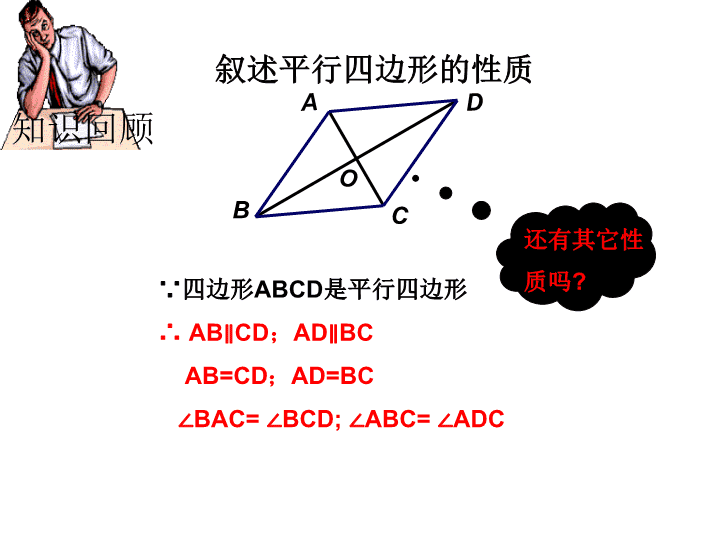 叙述平行四边形的性质ABDCO知识回顾∵四边形ABCD是平行四边形∴AB∥CD；AD∥BCAB=CD；AD=BC∠BAC=∠BCD;∠ABC=∠ADC还有其它性质吗? ACDBO已知：如图，ABCD的对角线AC、BD相交于点O.求证：OA=OC，OB=OD.平行四边形的对角线互相平分. 平行四边形的性质定理：平行四边形的对角线互相平分.符号语言：∵四边形ABCD是平行四边形OA=OCOB=OD∴ADBCO 例1.如图6-5，在平行四边形ABCD中，点O是对角线AC、BD的交点，过点O的直线分别与AD、BC交于点E、F.求证:OE=OF.探索发现，灵活运用 1.如图6-6,平行四边形ABCD的对角线AC、BD相交于点O,∠ADB=900,OA=6,0B=3.求AD和AC的长度.探索发现，灵活运用 巩固反馈，总结提高2．平行四边形ABCD的两条对角线相交于O，OA，OB，AB的长度分别为3cm、4cm、5cm，求其它各边以及两条对角线的长度。 ABCDO如图，在中，已知对角线AC和BD相交于O，△AOB的周长为15，AB=6,那么对角线AC与BD的和是多少？ABCD例2学以致用 变式、如上例1图,平行四边形ABCD的周长为60cm，对角线AC，BD相交于点O，△AOB的周长比△BOC的周长少8cm,求AB，BC的长．解： ∵四边形ABCD是平行四边形，∴AB=CD，AD=BC(平行四边形的对边平行).AO=CO，BO=DO(平行四边形的对角线互相平分).∵AB+BC+CD+DA=60，（BC+BO+CO）－（AB+AO+BO）=8，∴AB+BC=30，BC－AB=8，解得BC=19cm，AB=11cm．学以致用 如图，在ABCD中，对角线AC,BD交于点O，AC＝10，BD=8,则AD的取值范围是_________.ODBAC●1＜AD＜9 ACDBO●老大老四老三老二M老人分地合理吗？ ODBAC如图,在ABCD中,对角线AC﹑BD相交于点O,且AC+BD=20,△AOB的周长等于15,则CD=______.5练一练 小结与反思1、通过本节课的学习，你有什么收获？2、平行四边形的性质共有哪些？边：角：对角线：对边平行，对边相等对角相等，邻角互补对角线互相平分 图形名称文字语言图形语言符号语言平行四边形定义两组对边分别平行的四边形∵AB∥CD,AD∥BC∴…是平行四边形性质平行四边形的对边平行;对边相等;对角相等;对角线互相平分∵四边形ABCD是平行四边形∴AB∥CD,AD∥BCAB=CD,AD=BC∠A=∠C,∠B=∠DOA=OC,OB=ODＡＢＣＤＡＢＣＤＡＢＣＤO 成长的故事成长是缓缓流淌的溪流。悄然地，我们就长大了。成长，不仅意味着身体的成熟，更多是体现着你心理的变化，情感的丰富。学会了坚强，学会了坦然。成长是—个蜕变的过程，由简单到复杂，由幼稚至成熟。一季又一季美丽的鲜花，一代又一代美丽的成长故事，收集这些鲜花，串起这些故事，以“成长”为话题写一篇作文。 一、审题指导：1、说说什么叫“成长”？2、哪些算是成长呢？ A品德方面的成长：会帮助同学了 为父母做事了能恪守诺言坚持原则……B学习方面的成长：能坚持不懈了 自己的难题自己解决 能主动探索知识了  能体会到大人的苦心了  知道细心的重要……C能力方面的成长：学会了一项技能  能自己独自回家了会开展小队活动了 会为大家服务了 能耐心做事情……D友情方面的成长：会解决同学矛盾 会真心对待朋友  学会了谦让……E在失败与沮丧中的成长：失败中得到启发 摩擦中懂得谅解 矛盾中得到教训  后悔中得到成长 强调：我们还应该注意到“成长”是一种变化，是—个蜕变的过程，从无知到有知，从有错到认错，从没感受到感受深刻，我们在写作文时还要注意这种变化。 二、拟题指导1、掌握话题作文最基本最实用的拟题方法-----话题扩充法。A、话题+【    】  如：成长路上有你相伴B、【  】+话题   如：品味成长C、【  】+话题+【   】  如：承担，在成长路上 2、拟题欣赏成长的伙伴成长的快乐成长滋味成长的轨迹成长中的苦和乐我长大了品味成长成长的故事成长的烦恼成长时为自己喝彩成长的记忆成长的路上，我与书同行成长路上有爱 三、叙事类记叙文写作：如何把这些小事作为材料来写作文呢？请注意以下几点： 1,要交代清楚时间、地点、人物、事件，让读者明白文章写的是什么人，在什么时候，什么地方发生了怎样的事。2，记事中要围绕中心，抓住重点，不要面面俱到。重点部分（一般指事情发展高潮处）要详写，写具体，写详尽，给读者以深刻的印象。3，写事离不开写人，同此在记事过程中，一定要把人物的语言、神态、动作、心理活动等写细致，写逼真，这样才能表达出人物的思想品质，才能更好地表达这件事所包含的意义，即文章的中心思想。'