最新心理学趣味图片课件PPT.ppt 67页

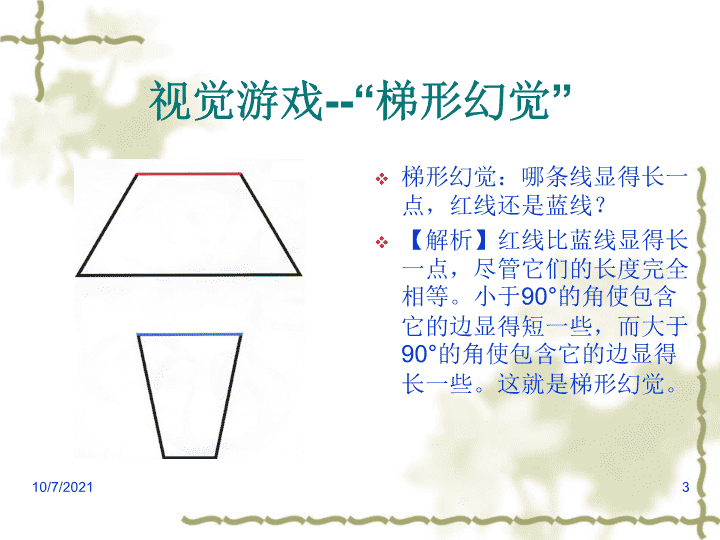
'心理学趣味图片 视觉游戏--“黑林图形”黑林图形：黑线看起来是不是向外弯曲的？【解析】黑线完全是笔直而平行的。这种经典幻觉由19世纪德国心理学家艾沃德·黑林首先发现。10/7/20212 视觉游戏--“梯形幻觉”梯形幻觉：哪条线显得长一点，红线还是蓝线？【解析】红线比蓝线显得长一点，尽管它们的长度完全相等。小于90°的角使包含它的边显得短一些，而大于90°的角使包含它的边显得长一些。这就是梯形幻觉。10/7/20213 视觉游戏--“两个圆”【解析】两个内部的圆大小完全一样。当一个圆被几个较大的同心圆包围时，它看起来要比那个被一些圆点包围的圆小一些。10/7/20217 视觉游戏--“扭曲的圆”韦德螺旋：这真是一个螺旋吗？【解析】英国视觉科学家、艺术家尼古拉斯·韦德向我们展示了他的弗雷泽螺旋幻觉的变体形式。虽然图形看起来像螺旋，但实际上它是一系列同心圆。10/7/20218 视觉游戏--“曲线正方形”曲线正方形：这些是完全的正方形吗？【解析】正方形看起来是变形了，但其实它们的边线都是笔直而彼此平行的。比尔·切斯塞尔创作了这个曲线幻觉的视觉艺术版本。10/7/20219 视觉游戏中间的确是个正圆，不相信用仪器量！！！10/7/202110 视觉游戏你能看出图中的横线是平行的吗？10/7/202111 甩甩头，画面动了！！！10/7/202112 甩甩头，画面动了！！！10/7/202113 看着黑点身体前后移动看着黑点身体前后移动看着黑点身体前后移动看着黑点身体前后移动看着黑点身体前后移动看着黑点身体前后移动10/7/202114 视觉游戏--“比泽尔德幻觉”比泽尔德幻觉：图中所有的红色看起来都一样吗？【解析】语境会影响你对颜色的感知。所有的红色都是完全一样的。这就是比泽尔德幻觉。10/7/202115 视觉游戏--“盒子幻觉”盒子幻觉：看立方体外侧面上的这个图形。哪条线与竖线垂直？哪条线不与竖线垂直？把立方体的边线遮住，你将发现你的感知发生了变化。【解析】盒子幻觉的感知提示为你确定图中心线段的位置提供了一个背景。离开盒子你的视觉系统就必须使用其他背景。这就是盒子幻觉。10/7/202116 视觉游戏--“赫尔曼·格瑞德幻觉”幻觉产生幻觉：这是一个精彩的幻觉产生幻觉的例子。在交叉部分你能看到微弱的蒙胧的小点。（赫尔曼·格瑞德幻觉）这些点又产生出一系列同心圆的印象。【解析】英国视觉科学家、艺术家尼古拉斯·韦德创作了这幅精彩的幻觉产生幻觉图。10/7/202117 视觉游戏--“共时对照幻觉”共时对照幻觉：交叉部分的白点是不是显得比白色方格更白更亮？【解析】白色方格看起来更白一点，尽管二者并没有区别。小白格看起来好像位于黑色背景上，这强化了每一个小方格和它背景之间的亮度对比。10/7/202118 视觉游戏--“米勒·莱尔幻觉”米勒·莱尔幻觉：哪条红线更长？【解析】信不信由你，两条红线完全等长。透视的运用大大地增强了传统的米勒·莱尔幻觉版本的效果。相形之下，传统的米勒·莱尔版本逊色不少。10/7/202119 视觉游戏--“方格幻觉”晃动的方格幻觉：这些方格是不是看起来有点彼此倾斜？【解析】这是一个定位对照幻觉的例子。两个方格邻边的定位差异，很可能被视觉系统的神经连接部分夸大了。神经连接部分有时候强化了感知的差异，这有助于我们察觉另外的微小事物。心理学家保罗·斯诺登和西门·沃特于1998年发现了晃动的方格幻觉。10/7/202120 视觉游戏--“曲线幻觉”【解析】当你的视网膜把边缘和轮廓译成密码，幻觉就偶然地现在视觉系统发生。这就是曲线幻觉。10/7/202121 视觉游戏--“完好的圆”【解析】虽然端点看起来不连在一起，左边弯曲部分也显得比右边的小一点，但其实这是一个完好的圆。10/7/202122 视觉游戏--“托兰斯肯弯曲幻觉”托兰斯肯弯曲幻觉：哪条线的曲线半径最大？【解析】这三个圆弧看起来弯曲度差别很大，但实际它们完全一样，只是下面两个比上面那个短一些。视觉神经末稍最开始只是按照短线段解释世界。当线段的相关位置在一个更大的空间范围延伸概括后，弯曲才被感知到。所以如果给定的是一条曲线的一小部分，你的视觉系统往往不能察觉它是曲线。10/7/202123 视觉游戏--“三角长度幻觉”三角长度幻觉：哪个颜色的线看起来更长？【解析】绿色线看起来比红色线长，虽然它们其实一样长。10/7/202124 柱子是圆的还是方的,别着急慢慢看......10/7/202125 视觉游戏--“爱之花”爱之花：你能看到玫瑰花瓣中的两个爱人吗？【解析】瑞士艺术家桑德罗·戴尔·普瑞特创作了这幅充满浪漫情调的、有歧义的、含义模棱两可的幻觉作品你能看出图中的横线是平行的吗？10/7/202126 视觉游戏--“身体的紫罗兰”身体的紫罗兰：你能在叶子中间找到三个隐藏的侧面人像吗？10/7/202127 视觉游戏--“隐藏的拿破仑”隐藏的拿破仑：你能发现站立的拿破仑像吗？这幅图形／背景幻觉图出现于拿破仑逝世后不久。【解析】拿破仑就藏在两树之间。两树的内侧树干勾勒出了站立的拿破仑像10/7/202128 视觉游戏--“鲁宾的面孔／花瓶幻觉”鲁宾的面孔／花瓶幻觉：你看的是一个花瓶还是两个人的头的侧面像？【解析】两种解读都能看到。但是，在任何时候，你都只能看见面孔或只能看见花瓶。如果你继续看，图形会自己调换以使你在面孔和花瓶之间只能选择看到一个。格式塔心理学家爱德加·鲁宾是这个经典的图形／背景幻觉图广为人知。鲁宾是从一张19世纪的智力玩具卡片上获取的灵感。10/7/202129 视觉游戏--“舞者与手势”舞者与手势：在瑞士艺术家桑德罗·戴尔·斯普瑞特创作的这幅有歧义的画中，手和舞者都呈现出优雅之态。10/7/202130 运动？静止？10/7/202131 运动？静止？10/7/202132 你知道周围有多少老人在朝他微笑吗？10/7/202133 如果你看见这个舞女是顺时针转，说明你用的是右脑；如果是逆时针转，说明你用的左脑。据说，14%的美国人可以两个方向都能看见。10/7/202134 帆船与桥10/7/202135 结婚真的等于下地狱吗？10/7/202136 镜子做的湖面10/7/202137 绝对数花你的眼睛！！！10/7/202138 看到大大的老人头没？10/7/202139 看到钓鱼人了吗？10/7/202140 楼上还是楼下？10/7/202141 能看到几张脸？10/7/202142 能看到一个女人吗？10/7/202143 你能看到几只海豚？10/7/202144 只看到放鸽子？10/7/202145 找到熊了吗？10/7/202146 你看到了几只鹿？10/7/202147 孕育生命10/7/202148 瀑布与传教士10/7/202149 如此观众10/7/202150 印第安人骑着马？还是骑着鹰？10/7/202151 树上？树下？10/7/202152 12人？13人？10/7/202153 函数的奇偶性数学必修1（A版）P33 教学目标知识与技能方面：1.使学生理解奇函数、偶函数的概念及其几何意义；2.使学生掌握判断函数奇偶性的方法。过程与方法方面：1.培养学生判断、推理的能力；2.通过教学，使学生明确奇（偶）函数概念的形成过程，强化数形结合、等价转化思想训练。情感态度价值观:使学生在学习过程中，欣赏数学美，体验数学的科学价值和应用价值，养成细心观察、认真分析、严谨论证的良好思维习惯和勇于探索的科学态度。 一、现实生活中的“美”的事例 二、函数图象的“美”xyOxyOf(x)=x2f(x)=|x|x…-2-1012…y……x…-2-1012…y……问题：1、对定义域中的每一个x，-x是否也在定义域内？2、f(x)与f(-x)的值有什么关系？ 赵州桥又名安济桥，建于隋炀帝大业年间(公元595-605)年间，是著名匠师李春建造。桥长64.40米，跨径37.02米，是当今世界上跨径最大、建造最早的单孔敞肩型石拱桥。这是世界造桥史的一个创造。(x,f(x))(-x,f(x))y=f(x)因为点M`在函数图象上，所以其坐标又为（-x，f（-x）） 函数y=f(x)的图象关于y轴对称1、对定义域中的每一个x，-x是也在定义域内；2、都有f(x)=f(-x)三、偶函数的定义如果对于函数f(x)的定义域内任意一个x，都有f(-x)=f(x)，那么函数f(x)就叫做偶函数（evenfunction）。 四、偶函数的判定（1）下列说法是否正确，为什么？（1）若f(－2)=f(2)，则函数f(x)是偶函数．（2）若f(－2)≠f(2)，则函数f(x)不是偶函数．（2）下列函数是否为偶函数，为什么？。（A）（B）（C）（D） Oyx123-1-2-3-1-2-3123（x，f（x））（-x，-f（x））因为点M`在函数图象上，所以其坐标又为（-x，f（-x）） 函数y=f(x)的图象关于原点对称1、对定义域中的每一个x，-x是也在定义域内；2、都有f(-x)=-f(x)五、奇函数的定义如果对于函数f(x)的定义域内任意一个x，都有f(-x)=-f(x)，那么函数f(x)就叫做奇函数(oddfunction)。 判定函数奇偶性基本方法:①定义法:先看定义域是否关于原点对称,再看f(-x)与f(x)的关系.②图象法:看图象是否关于原点或y轴对称. 六、应用:例1判断下列函数的奇偶性1.y=-2x2+1,x∈R;2.f(x)=-x｜x｜;3.y=-3x+1;4.f(x)=x2,x∈{-3,-2,-1,0,1,2};5.y=0,x∈[-1,1];是偶函数是奇函数不是奇函数也不是偶函数非奇非偶函数非奇非偶函数亦奇亦偶函数既是奇函数也是偶函数 例3如图是奇函数y=f(x)图象的一部分，试画出函数在y轴左边的图象。xy0例4已知y=f(x)是R上的奇函数，当x>0时，f(x)=x2+2x-1，求函数的表达式。 小结1、奇偶函数的定义；2、奇偶函数的判定。作业P39A6B3'