最新概率论与数理统计期末必备复习资料课件PPT.ppt 84页

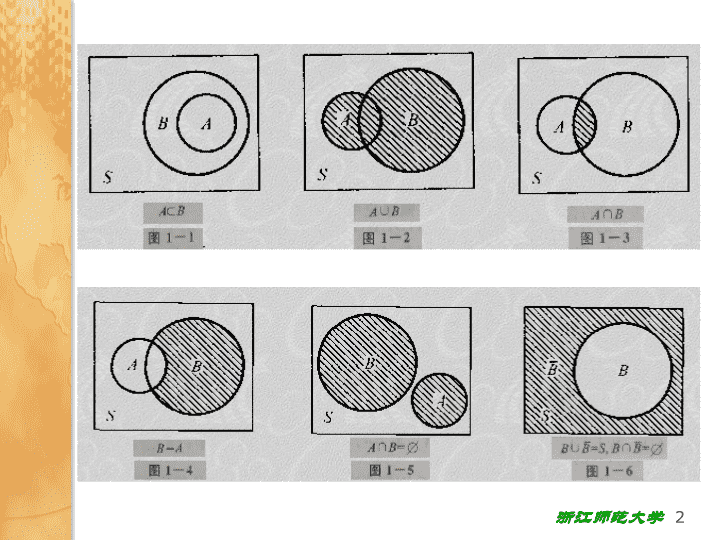
'概率论与数理统计期末必备复习资料 事件的运算律交换律：结合律：分配律：对偶律（DeMorgan德摩根律）：减法： 组合：从n个不同元素中取出m个元素并成一组(与顺序无关).组合数：从n个不同元素中取出m个元素的所有组合的个数，记为 等可能概型（古典概型）定义：具有以下性质的随机试验称为等可能概型试验的样本空间的元素只有有限个试验中每个基本事件发生的可能性相同等可能概型中事件概率的计算公式：n为随机试验的总的结果数，即样本点的总数，k为事件A包含的结果数。 定义：事件A已发生的条件下事件B发生的概率，称为条件概率，记为P(B|A)。例将一枚硬币抛掷两次，观察其出现正面的情况，设A={至少有一次为正面H}，B={两次掷出同一面}，求P(B|A)解：样本空间S={HH,HT,TH,TT},A={HH,HT,TH},B={HH,TT}。则可得：P(B|A)＝1/3条件概率的计算公式：条件概率 乘法定理：设P(A)>0，则有P(AB)=P(B|A)P(A)推广：P(AB)>0，则有P(ABC)=P(C|AB)P(AB)=P(C|AB)P(B|A)P(A)设为n个事件，且 全概率公式划分：设S为试验E的样本空间，为E的一组事件，若则称为样本空间S的一个划分.例E：掷骰子观察点数是S的一个划分不是S的一个划分 全概率公式定理：设随机试验E的样本空间为S，A为E的事件.为S的一个划分，且则，称之为全概率公式。注：全概率公式给出我们一个用来计算在众多原因的作用下事件A发生概率的方法.（由因得果） 贝叶斯公式（由果溯因）设E的样本空间为S，A为E的事件.为S的一个划分，且，则为贝叶斯（Bayes）公式.称为先验概率；称为后验概率. 条件概率条件概率小结缩减样本空间定义式乘法公式全概率公式贝叶斯公式 独立性独立事件：两事件A、B，A发生对B发生没有影响，B发生也对A没有影响，则称两事件相互独立.即P(A|B)=P(A)且P(B|A)=P(B)，则P(AB)=P(A)P(B|A)=P(A)P(B)例抛甲，乙两枚硬币，A={甲出现正面H}，B={乙出现正面H}，问A，B同时发生的概率.定理四对事件中有一对相互独立，则另外三对也相互独立.独立与互斥的区别：A，B相互独立：P(AB)=P(A)P(B)；A，B互斥：P(AB)=0。 多个事件的独立 定义随机试验的结果可以用一个实值变量表示，这个变量的取值是随机的，但又服从一定的统计规律性，这种变量称为随机变量，通常用X，Y，Z表示。中心问题：将试验结果数量化随机变量分为离散型和连续型：离散型：X的取值是有限个或可列无限个。连续型：X的取值是连续的。esxX=f(e)—为S上的单值函数，X为实数 分布律称为离散型随机变量X的分布律，分布律可用列表的方式直观的表示出来X1、写出可能取值－－即写出了样本点2、写出相应的概率－－即写出了每一个样本点出现的概率分布律（概率分布） 01X1.两点分布，又称为(0-1)分布(0-1)分布的分布律为也可以写为对随机实验，若样本空间只包括两个元素，即，则一定能在S上定义一个服从(0-1)分布的随机变量，令例抛硬币一次，定义随机变量X为出现正面的次数，则01X1-pp三种重要的离散型随机变量 2.二项分布随机试验E只有两个可能结果：A和，则称E为伯努利试验。设P(A)=p(00，有切比雪夫不等式的等价形式注：1.切比雪夫不等式可用来估计不是服从正态分布的随机变量落在E(X)附近的概率。2.切比雪夫不等式的主要作用是进行概率论的理论研究。 1.样本的定义（独立同分布）2.统计量的定义和判别3.统计学三大分布的定义和图形轮廓4.三大分布的分位点定义第六章样本及抽样分布 样本总体：试验中全部可能的观察值（研究对象的全体，如一批灯泡），一个总体对应于一个随机变量X。个体：每个可能观察值称为个体（组成总体的每个元素，如某个灯泡）抽样：从总体X中抽取有限个个体对总体进行观察的取值过程。随机样本：随机抽取的n个个体的集合(X1,X2,…,Xn),n为样本容量。简单随机样本：满足以下两个条件的随机样本(X1,X2,…,Xn)1.每个Xi与X同分布2.X1,X2,…,Xn是相互独立的随机变量[说明]：后面提到的样本均指简单随机样本。 统计量：设是总体X的样本，则函数如果不包含任何未知参数则称为样本的一个统计量。统计量简言之，样本的不含任何未知参数的函数。 常用的统计量样本平均值：样本方差：样本均方差：样本k阶(原点)矩：样本k阶中心矩： 统计学三大分布 例如： 1.矩估计法（三步法）2.最大似然估计法（三步法）3.估计量三大评选标准的定义及证明（无偏性、有效性、相合性）4.单个正态总体均值和方差的区间估计第七章参数估计 矩估计法 最大似然估计的求法写出似然函数求，使得为的最大值，求法如下：求使得方程又在同一处取得极值，因此，的最大似然估计值可从方程中求得称为似然方程1.单参数 2.双参数似然函数似然方程最大似然估计法 估计量的评选标准对总体的未知参数可用不同方法求得不同的估计量，如何评价好坏？通常用三条标准检验：无偏性，有效性，相合性无偏性 有效性 相合性 正态总体均值与方差的区间估计 ThankYou! 1.假设检验的定义2.假设检验的三步法3.单个正态总体均值和方差的假设检验统计量和拒绝域第八章假设检验 问题：设X～，已知，未知。给定，问？假设称为原假设(零假设)，称为备择假设(对立假设)。通过某种方式确定常数k。若，则接受，若，则拒绝(接受)。犯两类错误的概率：若为真而被拒绝，我们称为犯第一类错误(又称犯“弃真”错误，其概率记为。一般，0.1.若为假而被接受，我们称为犯第二类错误(又称犯“取伪”错误，其概率记为。 记取检验统计量为我们称拒绝的区域W为拒绝域，将接受的区域称为接受域。的拒绝域为W={｜Z｜}，的接受域为={｜Z｜<}。即 0000<0>0Z检验法(2已知)原假设H0备择假设H1检验统计量及其H0为真时的分布拒绝域 0000<0>0t检验法(2未知)原假设H0备择假设H1检验统计量及其H0为真时的分布拒绝域 2022>022<022022=02202原假设H0备择假设H1检验统计量及其在H0为真时的分布拒绝域(未知)关于2的检验（检验法） 基本初等函数导数公式表1函数y=f(x)导函数y=cy=xα(α∈R)y=ax(a>0,a≠0)y=logax(a>0,a≠1,x>0y=lnx 函数y=f(x)导函数y=sinxy=cosxy=tanxy=cotx基本初等函数导数公式表2 基本求导公式 函数的和、差、积、商的求导法则1.可以推广到有限个2.3.特别地,C为常数. 白色通用Loremipsumdolorsitamet,consecteturadipisicingelit. 教师活动教学组织过程初识知识学生活动课前知识小测课中知识深化论坛话题提出知识要点深化课前资源浏览导图软件学习预习知识小测课前任务布置参与论坛讨论收集问题备课话题讨论案例资源讲解组织课堂讨论分析问题解惑课堂讨论分析问题任务小结加深知识理解软件梳理结论知识应用提升应用知识分析知识点PPT及微课视频任务一知识点小测试题论坛话题PPT任务一PPT及微课视频案例录屏视频学生活动PPT以及录屏教学资源任务一：节事活动市场调查概述软件学习思维导图软件录屏视频1课时准备好思维导图软件 教师活动教学组织过程知识梳理学生活动课后预习任务二课中任务知识深化案例分析论坛话题提出知识要点深化学习导图软件思考提出疑问预习知识小测要求结论整理参与论坛讨论收集问题备课话题讨论案例资源讲解组织课堂讨论分析问题解惑课堂讨论分析问题任务小结加深知识理解整理讨论结论知识应用提升应用知识分析思维导图软件录屏视频教学资源教学视频录屏视频任务知识点小测试 课中任务呈现知识呈现提出任务要求录屏知识呈现组织课堂讨论知识深化总结课堂讨论梳理知识任务小结了解可行性研究深化知识应用思考知识应用分组讨论梳理课堂任务PPT以及表格任务四微课视频及PPT可行性研究音频任务四：节事活动可行性研究的内容应用微知库笔记记载课后知识梳理预习知识2课时限定时间小测布置预习任务课前资源浏览任务四知识点小测试题深化知识应用任务四PPT及微课视频微课知识呈现 任务一任务二任务三任务四任务五 明确节事活动策划的重点以时间为主以热点为主以亮点为主'