最新第25课时23.2中心对称(1)课件PPT.ppt 30页

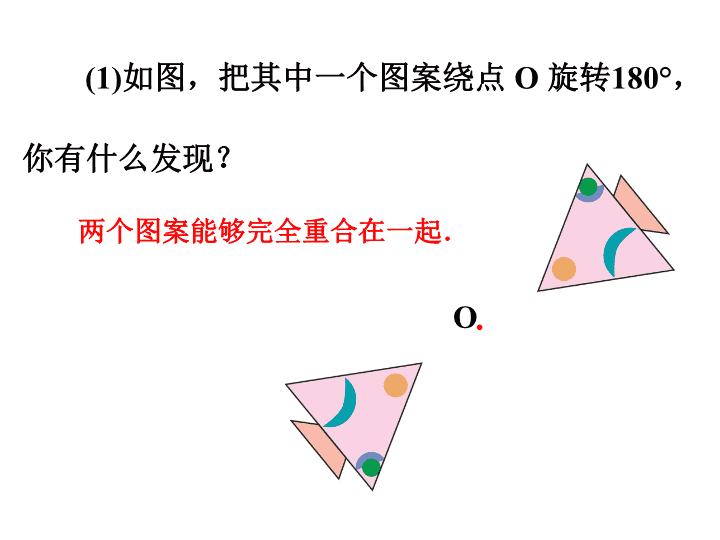
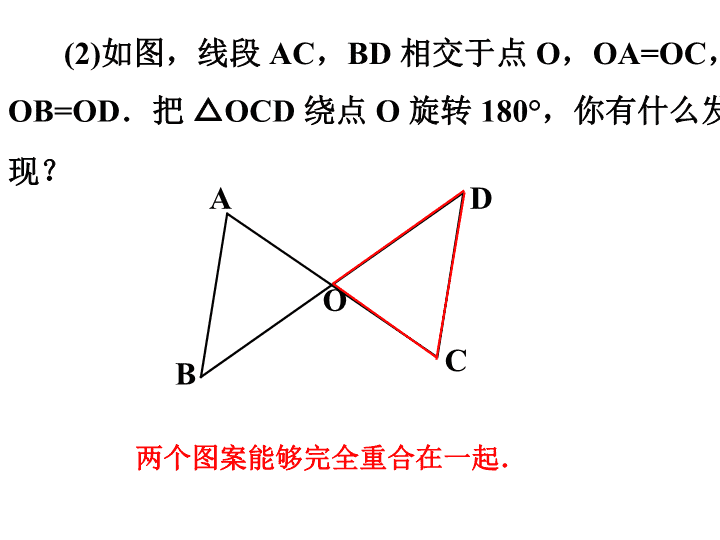
'第25课时23.2中心对称(1) (1)如图，把其中一个图案绕点O旋转180°，你有什么发现？两个图案能够完全重合在一起．O (2)如图，线段AC，BD相交于点O，OA=OC，OB=OD．把△OCD绕点O旋转180°，你有什么发现？两个图案能够完全重合在一起．DABCO CABC＇A′B′O中心对称是特殊的旋转，它有哪些性质？ (1)点O在线段AA＇上吗？如果在，在什么位置？(2)△AOB和△A′OB′有什么关系？(3)你能从这个探究中得到什么结论？ABOB′A′ (1)中心对称的两个图形，对称点所连线段都经过对称中心，而且被对称中心所平分；(2)中心对称的两个图形是全等图形．中心对称的性质ABOB′A′ 例1(1)如左图，选择点O为对称中心，画出点A关于点O的对称点A＇；(2)如右图，选择点O为对称中心，画出与△ABC关于点O对称的△A′B′C′．AOOABC 例1(1)如左图，选择点O为对称中心，画出点A关于点O的对称点A＇；AO画法：1.连接OA，A＇2.延长AO，在AO的延长线上截取OA＇，使OA＇=OA.则点A＇为所求. 例1(2)如右图，选择点O为对称中心，画出与△ABC关于点O对称的△A′B′C′．OABCB′C′画法：1.分别作点A，B，C关于点O为对称中心的对称点A′、B′、C′.A′2.连接A′B′、B′C′、C′A′，则△A′B′C′为所求. (1)如图，已知△ABC与△DEF中心对称，点A和点D是对称点，画出对称中心O．ABCDEFO解：连接AD，CF，AD与CF交于点O，则点O为所求. (2)如图，以顶点A为对称中心，画一个与已知四边形ABCD成中心对称的图形．ABCDB′c′D′四边形AB′C′D′为所求． 小结(1)本节课学了哪些主要内容？(2)怎样画一个图形关于一个点的对称图形？ 6．布置作业教科书第66页，练习1，2题． 本节课从旋转变换引入中心对称的概念，先让学生从旋转的角度观察两个图形之间的关系，类比旋转得出中心对称的定义，渗透了从一般到特殊的思想方法．在此基础上，通过探究成中心对称的两个图形的对称中心与对应点所连线段之间的关系得到中心对称的性质，并能运用中心对称的性质画出一个图形关于某一点中心对称的对称图形．课件说明 学习目标：1．知道中心对称的概念，能正确表述中心对称的性　质；2．会画一个图形关于某一点中心对称的对称图形．学习重点：中心对称的概念和性质．课件说明 16.3二次根式的加减乘除混合运算 1、单项式与多项式、多项式与多项式的乘法法则法则分别是什么?2、多项式除以单项式的除法法则是什么?m(a+b+c)=ma+mb+mc；(m+n)(a+b)=ma+mb+na+nb(ma+mb+mc)÷m=a+b+c温故而知新 分配律单×多转化前面两个问题的思路是：思考：若把字母a,b,c,m都用二次根式来代替(每个同学任选一组)，然后对比归纳，你们发现了什么？单×单 探索新知二次根式的混合运算二次根式的加、减、乘、除混合运算与整式运算一样，体现在：运算律、运算顺序、乘法法则等仍然适用.例1计算：解： 二次根式的混合运算，先要弄清运算种类，再确定运算顺序：先乘除，再加减，有括号的要算括号内的，最后按照二次根式的相应的运算法则进行.归纳解：此处类比“多项式×多项式”即(x+a)(x+b)=x2+(a+b)x+ab. 解：(1)原式(2)原式闯关一、基础闯关相信你能过关！有绝对值符号的，同括号一样，先去绝对值，注意去掉绝对值后，得到的数应该为正数.归纳1、比一比，看谁算得又快又准！ （1）整式乘法运算中的乘法公式有哪些?平方差公式：(a+b)(a-b)=a2-b2;完全平方公式：(a+b)2=a2+2ab+b2;(a-b)2=a2-2ab+b2.2、利用乘法公式进行二次根式的运算（2）整式的乘法公式对于二次根式的运算同样适用。 例2计算：解：归纳进行二次根式的混合运算时，一般先将二次根式转化为最简二次根式，再根据题目的特点确定合适的运算方法，同时要灵活运用乘法公式，因式分解等来简化运算. 闯关一、基础闯关相信你能过关！2、比一比，看谁算得又快又准！ 1、已知试求x2+2xy+y2的值.解：x2+2xy+y2=（x+y)2把代入上式得原式=闯关二、能力提升闯关你过关了吗？2、已知的整数部分是a,小数部分是b,求a2-b2的值.解： 3、阅读下列材料，然后回答问题：在进行类似于二次根式的运算时，通常有如下方法将其进一步化简：运用以上规律化简： 课堂小结二次根式混合运算乘法公式化简求值分母有理化化简已知条件和所求代数式(a+b)(a-b)=a2-b2(a+b)2=a2+2ab+b2(a-b)2=a2-2ab+b2(x+a)(x+b)=x2+(a+b)x+ab'